Conserve Energy?
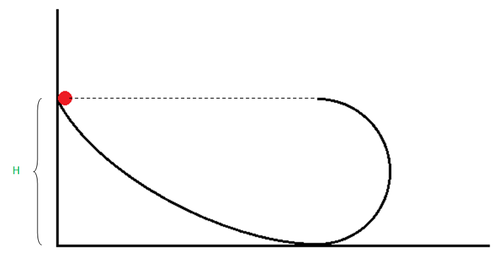 A small body starts sliding from the height
H
down a fixed inclined groove passing into a half circle of radius
2
H
. Find the speed of body (in m/s) when it reaches the highest point (w.r.t the lowest point of circular path) of its trajectory after entering into the half circle.
A small body starts sliding from the height
H
down a fixed inclined groove passing into a half circle of radius
2
H
. Find the speed of body (in m/s) when it reaches the highest point (w.r.t the lowest point of circular path) of its trajectory after entering into the half circle.
Given Data : H = 5 . 4 m & g = 9 . 8 m s − 2
Try more from my set Classical Mechanics Problems .
The answer is 2.8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Nice question bro! :) I thought that I have to find the velocity at the highest point of the trajectory wrt the velocity at the lowest point of the trajectory. That's why I solved it in second attempt.
Log in to reply
Thanks. I also had hard time solving this question on first attempt. That's why I posted it here.
Log in to reply
Nice question @Purushottam Abhisheikh !!:)
Better than me... My first attempt I accidentally solved for the highest point it reached! (5 meters above bottom of the circle) I am not good at reading carefully... :)
Log in to reply
I think you should try this . :D
Log in to reply
@Satvik Pandey – Hahaha, my effort was not wasted! :D
Log in to reply
@Nathanael Case – Efforts are never wasted. :D :)
Log in to reply
@Satvik Pandey – Badi baate
Log in to reply
@Kushal Patankar – Yeah! badi baate. But it sounds good. Isn't it? :D
Log in to reply
@Satvik Pandey – Yep. These questions I did when vertical circular motion was going on in class. So not felt that tough.
Log in to reply
@Kushal Patankar – Yes it easy to solve if one realize that ball would left contact with the track.
My bad I solved it in 2nd attempt. I thought that I have to find relative velocity of the ball at the highest point of the trajectory wrt its velocity at the lowest point of the trajectory. That sentence inside the bracket confused me. :(
What a question!!!!
The question asks for speed. The solution computes the speed at the point of loss of contact with the surface, but the answer is given as the horizontal component of velocity at that point. It should be the magnitude of the resultant velocity. In my opinion, the answer should be 4.2 m/s(V) and not 2.8m/s (V*cos(theta)). (refer solution)
When one says speed, one usually means the resultant magnitude of the velocity vector. If the answer is the horizontal component of velocity at the point of loss of contact, this requirement needs to be explicitly specified in the problem statement. I entered my answer as 4.2 m/s.
Please correct me if I am wrong.
Log in to reply
Exactly.Yes you are correct. I think the question has inadequate data.
The question asks for the speed at the highest point of the trajectory. Obviously the particle won't stop moving just after losing the contact with the surface. It will start a projectile motion from there.
Let H = 2 R .
So, velocity of particle at the lowest point of the semicircle will be V o = 4 g R . As we all know that this velocity is insufficient for the particle to go to the topmost point of the semicircle (The particle requires V o = 5 g R to go to top). Hence it will leave the semicircle at some point and start projectile motion. Let this point make an angle θ with vertical and velocity of particle at this point be V .
Since at this point particle just leave the semicircle so normal reaction given by the semicircle on the particle would be zero
⟹ m g c o s θ = R m V 2
⟹ g R c o s θ = V 2 …………………….. (i)
By conservation of energy,
2 1 m V o 2 = m g R ( 1 + c o s θ ) + 2 1 m V 2
⟹ 4 g R = 2 g R ( 1 + c o s θ ) + V 2
⟹ 2 g R = 3 V 2
or V = 3 2 g R
and c o s θ = 3 2
And velocity of particle at highest point of its trajectory would be V m a x = V c o s θ = 3 2 3 2 g R = 3 2 3 g H .
Putting all the values we get V m a x = 2 . 8 m / s