The Particle Race begins!

I will be dividing the solution into two parts. The first part will deal with the mathematical computation of the difference of time which will directly tell us which particle reaches its destination first. The second part will describe a more theoretical reasoning behind the outcome, that a person can infer without any calculations. $\text{ PART 1: Computation}$

Let the time taken for particle $P$ to reach point $B$ be $T_{P}$ . Let it be $T_{Q}$ for particle $Q$ .

$\bullet$ Since particle $Q$ moves with uniform velocity, $T_{Q} = \dfrac{Distance_{total}}{|v|}=\dfrac{2R}{|v|}=8seconds$

$\bullet$ Now for particle $P$ . Let the center of the hemisphere be $O$ and its lowermost point be $X$ . Now take any arbitrary point $Y$ , on arc $AX$ .Drop a perpendicular $YZ$ on $OA$ . Let the velocity of particle $P$ at point $Y$ be $v'$ .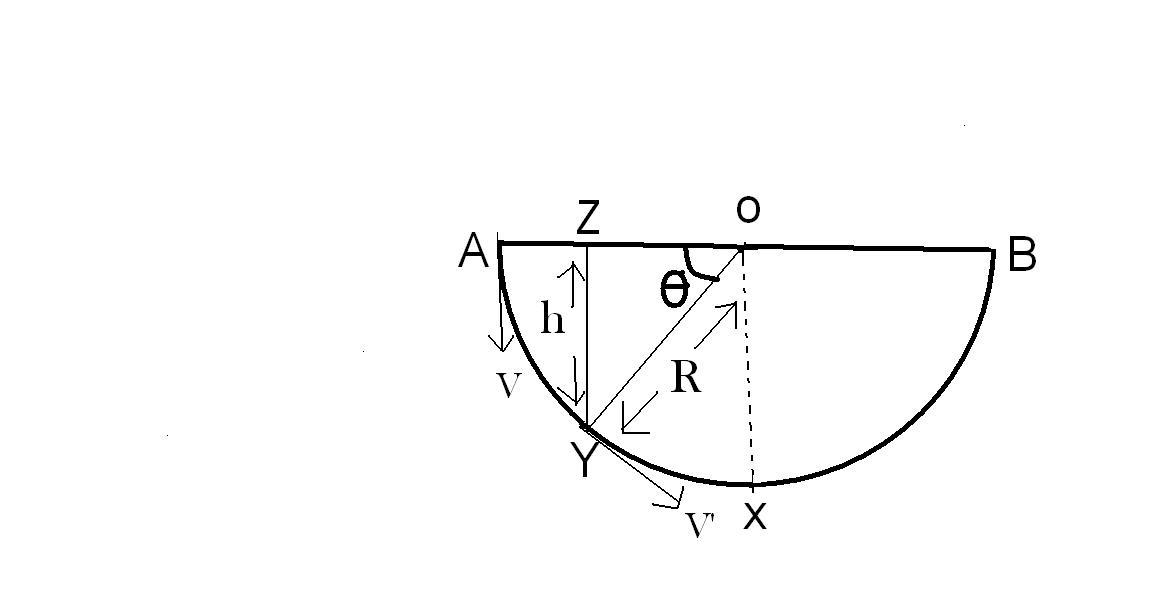

Join points $O , Z, Y$ to form right $\Delta{OZY}$ , right-angled at point $Z$ . Mark $\angle{YOZ}=\theta$ and length $YZ=h$ . Therefore $\sin(\theta)= \dfrac{h}{R} => h=R\sin(\theta)$

By conserving mechanical energy along this path-length $(AY)$ , We have : $\dfrac{1}{2}m(v'^{2}-v^2)= mgh=mgRsin(\theta)$ => $v'= \sqrt{2gR\sin(\theta)+v^{2}}$

For calculating the final time, we need to an introduce a quantity that would bring time in the equation as a differential element. Since $\theta$ is changing with position and time, we can conveniently introduce Angular velocity(at point $Y$ ). Therefore; $\omega=\dfrac{d\theta}{dt}= \dfrac{v'}{R}$ => $\dfrac{Rd\theta}{v'}=\dfrac{Rd\theta}{\sqrt{2gR\sin(\theta)+v^{2}}}=dt$ . Integrating $dt$ from $0$ to $t'$ , LHS from $0$ to $\dfrac{\pi}{2}$ , we get: $\int_{0}^{t'}dt=\int_{0}^{\pi/2}\dfrac{Rd\theta}{\sqrt{2gR\sin(\theta)+v^{2}}}$ => $t'=\int_{0}^{\pi/2}\dfrac{20d\theta}{\sqrt{400\sin(\theta)+25}}=2.16032 seconds$ . Since this time, $t'$ is is calculated from $0$ to $\dfrac{\pi}{2}$ i.e half the total distance, we need to double this time to get $T_{P}$ . Therefore, $T_{P}=2t'=4.32064 seconds$

Hence, $T_{Q}>T_{P}$ and; $T_{Q}-T_{P}= 8- 4.32064= 3.69736 seconds$

$\therefore \text{Final answer}= 10.73+3.69= 14.432 :)$ $\text { PART 2: Theoretical Reasoning}$

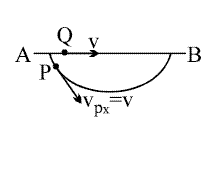
Draw the $\text{Free Body Diagram}$ for particle $P$ at any point(say point $'Y'$ for convenience).There is a component of normal $N\sin \theta$ in horizontal direction .Even though the magnitude of this force decreases as the particle slides down ,still it accelerates the particle in horizontal direction till it reaches the bottom .The horizontal component of velocity at any instant during the downward journey ,say $V_{Px}$ will be greater than $'V$ ' .

During the upward journey,it is the same component of normal force $N\sin \theta$ which decelerates the particle , till it reaches the opposite point to the initial point.Here either by conservation of energy or by symmetry we can say that the velocity of the particle will be same as that of the initial point .

So we can infer that the horizontal component of velocity will always be greater than $'V'$ during the entire journey(except at $t=0$ and $t=t$ ). $V_{Px} > V$ . The average horizontal speed of the particle is greater than $'V'$ .

Also ,in case of $Q$ there is no horizontal acceleration,hence velocity of $V_{Q}=V$ . The horizontal distances are same in both the cases ,hence $T_{Q}>T_{P} :)$