A classical mechanics problem by Steven Chase
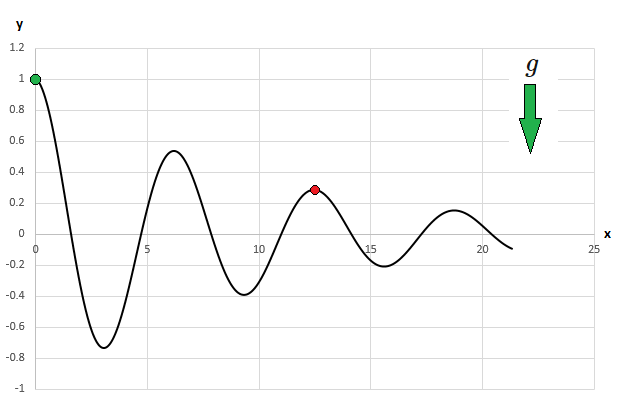
A bead slides down a friction-less wire in the shape of the following curve, where is the horizontal direction and is the vertical direction.
There is a uniform downward gravitational acceleration .
The bead starts at rest at .
What is the magnitude of the net force on the bead when it is at the peak (zero-slope) in the vicinity of ? Give your answer to 3 decimal places.
The answer is 4.125.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The first derivative of the function is:
d x d y = e − x / 1 0 [ − s i n ( x ) − 1 0 1 c o s ( x ) ]
The second derivative of the function is:
d x 2 d 2 y = e − x / 1 0 [ − c o s ( x ) + 1 0 1 s i n ( x ) + 1 0 1 s i n ( x ) + 1 0 0 1 c o s ( x ) ] e − x / 1 0 [ 5 1 s i n ( x ) − 1 0 0 9 9 c o s ( x ) ]
Determine where the derivative equals zero:
− s i n ( x ) − 1 0 1 c o s ( x ) = 0 ⟹ x = a t a n ( − 1 0 1 ) ± 2 π n
The x -coordinate of the peak near x = 4 π is:
x p = a t a n ( − 1 0 1 ) + 4 π
In general, there may be both normal and tangential forces at this point. We can rule out the presence of a tangential force using the following argument (note that the velocity is purely horizontal at the peak):
K i n e t i c E n e r g y = E = 2 1 m v 2 = m g ( 1 − y ) d t d E = − m g d t d y = 0 ( f o r x = x p ) d t d E = d v d E d t d v = m v d t d v = 0 ⟹ d t d v = 0 ⟹ F t a n g e n t i a l = 0
So the net force is equal to the normal force at the peak. We can use the familiar equation:
F n o r m a l = m R v 2
Except that here, R is the radius of curvature at that point. The general formula is given below (the apostrophes denote derivatives):
R c u r v a t u r e = ∣ ∣ ∣ y ′ ′ ( 1 + y ′ 2 ) 3 / 2 ∣ ∣ ∣
Since the first derivative is zero, this reduces to:
R c u r v a t u r e = ∣ ∣ ∣ y ′ ′ 1 ∣ ∣ ∣
The normal force is then:
F n o r m a l = m v 2 ∣ y ′ ′ ∣ = 2 m g ( 1 − y ) ∣ y ′ ′ ∣
Using the above expressions for y and y ′ ′ and plugging in numbers gives F n o r m a l = F t o t a l ≈ 4 . 1 2 5 . I also confirmed this result by numerically differentiating the velocity.