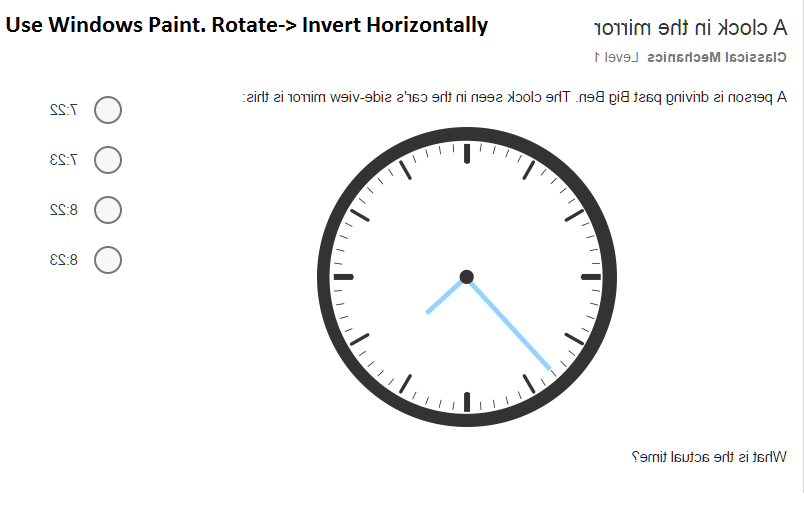
A clock in the mirror
A person is driving past a clock tower. The clock seen in the car's side-view mirror is this:
What is the actual time?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
I've updated my solution with clarification about assumptions over the orientation of the mirror, and an additional section detailing what would happen should the orientation of the mirror be 'abnormal'.
Log in to reply
Good point about the orientation of the mirror. It can be challenging to figure out the reflection axis from the orientation of the mirror.
subtract 4:37 from 12:00 hours= 7:23
Log in to reply
Better to write your own solution, than have it hidden away in the comments section, no?
Log in to reply
the mobile app doesn't have an add your own solution button -.-
Log in to reply
@Jerry McKenzie – That's not true. When you click the [Discuss solutions] button, you can then submit your own solution - both in the app, and the mobile version of the website in a browser (at least in the Chrome browser).
Log in to reply
@Jonathan Quarrie – I've always had to log in on my desktop to post solutions. I guess I have a bad app -.-
Log in to reply
@Jerry McKenzie – I only recently installed the app (to check this theory). Maybe you just need to update it.
@Jerry McKenzie – We closed off adding solutions to past Problems of the week.
Can you confirm that you're able to add a solution to this week's set? If not, please send me a screenshot. You can email me at Calvin at Brilliant.org.
12:00 - 4:37 = 7:63. Then how did you get 7:23 by subtraction?
Log in to reply
Because there are 60 minutes in an hour, not 100.
Log in to reply
@Jonathan Quarrie – Ahh, I see. then we will get the answer if we subtract 4:37 from 11:60 that is 11:60 - 4:37 = 7:23.
Log in to reply
@Rohit Gupta – Conventionally, 11:60 is 12:00, so yes.
With the same assumation i solved it by lateral shift property of the mirror. :)
Log in to reply
Are you referring to the lateral inversion property of the mirror that is left appears right and right appears left?
Doesn't this mean that a car coming from the right will appear to be coming from the left? Isn't this dangerous?
What if you are on a mac or are using the app?
Cheap? Cheating? Genius?? I don't know, but well done on using technology to figure it out!!
Why does inverting horizontally give the actual time, but inverting in any other direction does not?
Log in to reply
see dihedral groups, specifically D 4 . If the order of numbers is clockwise then the image was rotated, otherwise if the numbers have reversed to counterclockwise, then they must have been reflected, as in with the side view mirror.
Log in to reply
I don't get it, how does D 4 explain why we should invert it horizontally? According to D 4 , we can invert it vertically too, but that does not give the correct answer. I feel that the position of the mirror helps determine the axis of inversion.
Also, in this case, I think that since there are twelve numbers on the clock, so wouldn't D 1 2 would be more apt? Thanks
Log in to reply
@Pranshu Gaba – I usually use D 4 to introduce visual representations. More clearly in optics we notice that the image has been inverted in the depth dimension. But in such an inversion, our minds still think in terms of the "right hand rule" while in fact the imaginary image is in a "left handed" visual perception field. Since in a mirror we still interpret up as up and down as down our minds flip left from right more often then up from down. You could flip horizontally, but the clock would still function (in the imaginary image in the mirror) in a counter clockwise direction.
I just used a mirror!😅
.32:7 won si emit ehT
The time shown on the diagram is 4:37, but this is a reflection of the actual time, so imagine how many whole hours are left between 6 o'clock and 4:37 and that is 1 hour with a remainder of 23 mins. Therefore add 1 hour and 23 mins to 6:00 to give you 7:23.
Could you explain why are we comparing the time in the diagram with 6 o'clock?
Log in to reply
you could do it with 12 as well, just noting that a reflection means to subtract not add. i.e. 4:37 from 12 is 60-37=23 minutes and 11 (since we borrowed 60 mins from the 12th hour), 11-4=7.. 7:23
1 2 : 0 0 − 4 : 2 3 0 7 : 2 4
Log in to reply
Don't you mean 12:00 - 4:37 = 7:23
Log in to reply
@Abidur Rahman – yea i wanted to right cancel to, like i do in textstudio :P. if your interested its the cancel package. I wanted to mark out 12 and canel to 11 while cancelling 00 to 60.
The reflection of the clock happens along the line of symmetry i.e. imagine a line cutting the 6:00 and 12:00. Now think of the time as co-ordinates on a circle graph. The x-coordinate would be 4.23, calculate the distance from the point to the line of symmetry then add that distance from the line of symmetry i.e. 6:00-4:23 = 1hr 24 mins 6:00 + 1hr 24 mins = 7:24
I clicked on the right answer but it did not take, then I clicked on the wrong answer on my iPad and it went through informing me that I got it all wrong. Now I am thorougly unsettled :)
Mirror= Horizontally inverted
The orientation of the mirror dictates the plane of inversion.
Actually if you have mirror nearby put it in front as the mirror image of the mirror image is the actual image
Or do like this:. Make horizontal lines from the points where the lines of hour hand and minute hand intersect the circle(the given time) and the points where our horizontal line intersect is the actual time
Yes, this is the simplest way :) The mirror image of the mirror image would give back the actual time.
I spent a little time thinking about how to find the answer by Geometry, but the fastest solution was to use the Theorem of Common Sense - I got a Mirror. However, I still got the answer wrong, because the Mirror detail was not clear enough to see the exact minute hand. So, I just looked at the Screen Clock and it appeared to be 4:37, so, I just selected 4:23. Off by a Minute. So the THEOREM of COMMON SENSE also has it's issues.
Relevant wiki: Mirrors
Assuming that the the side-view mirror has a normal orientation, such that a horizontal reflection (across the vertical axis) occurs - 7 : 2 3
If the side-view mirror were abnormally oriented - parallel to the ground - a vertical reflection would occur (across the horizontal axis), and the reflected hour hand and minute hand would be of a nonsensical actual time in relation to one another.