1000-Point Star
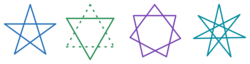 Typical "stars" are drawn in connected, but not repeated, line segments. For example, a 5-point star is drawn as such - line segments AC, CE, EB, BD, DA. The segments must always alternate a constant number of points (in the above case, skipping 1 point in between).
Given the information that there is only 1 way to draw a 5-point star, and that there is NO way to draw a 6-point star (in continuous lines, that is), and there are 2 ways to draw a 7-point star, how many different ways are there to draw a 1000-point star?
Typical "stars" are drawn in connected, but not repeated, line segments. For example, a 5-point star is drawn as such - line segments AC, CE, EB, BD, DA. The segments must always alternate a constant number of points (in the above case, skipping 1 point in between).
Given the information that there is only 1 way to draw a 5-point star, and that there is NO way to draw a 6-point star (in continuous lines, that is), and there are 2 ways to draw a 7-point star, how many different ways are there to draw a 1000-point star?
The answer is 199.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Can u explain why u used the Euler function in this case?
Log in to reply
A way of constructing the star is joining vertices clockwise and skipping the same number of vertices each time. For instance, with 7 vertices you can take the first vertex, then join it with the third one skipping the second one, then join it with the fifth one skipping the forth one, then the seventh one skipping the sixth one, then the second one, then the forth one, then the sixth one and finally you go to the first one. Nevertheless the leap you do every time (2 in the example) must be coprime with 1 0 0 0 since otherwise you will get that the cycle ends without using all vertices, so the Euler function appears in a natural way. For n vertices, the formula would be 2 φ ( n ) − 2 .
value of euler function?
Shouldn't it be 0, because the no. of points are even.. so it should be the same case as of 6 points.... hence, there would be no star with continuous lines..
Log in to reply
No. Look up for n=8. Search Google for 8 pointed star.
The vertices of an n-pointed star are the vertices of a regular n-gon, numbered 0 through n-1 in clockwise order. The star is determined by choosing a vertex m and drawing the line segments from 0 to m, from m to 2m, from 2m to 3m, and (n-1)m to 0, where all numbers are reduced modulo m. In order for the figure to satisfy our conditions, m must be relatively prime to n and not equal to 1 or m-1.
Thats the most exact way of solving it. I feel that the question should have been posted in number theory rather than combinatorics.
First, let's examine the 5-point star and why there is only that one, described, way to draw it. Starting at A, you cannot go straight to point B, otherwise you will have a pentagon, not a star. Same with point E. AC and AD (and their progressions) yield identical pictures (notice that the last segment in the AC one is DA, literally reverse all the letters to get AD ending in CA).
Now, for a 6-point star, there are points A, B, C, D, E, and F. Starting at A, we cannot go to B or F, because then we have a hexagon. If we go AC, then we must go CE, then CA... making a triangle, not a 6-point star. Going backwards, AE, EC, EA; mirror image. If we skip 2 points, we go AD, then DA, a straight line, hardly a 6-point star.
For a 7-point star, A-G, AB and AG are not possible, as that's a heptagon. AC, CE, EG, GB, BD, DF, FA is one way to draw the star, skipping one point in between. Also, AD, DG, GC, CF, FB, BE, EA, skipping two points in between each, is the other way. The last two line possibilities, AF and AE are mirror images of the two working scenarios.
Examining the above information a little more deeply, we see that we must divide all possible drawings by two, to get rid of the mirror images. Also, we cannot use the point immediately to the left, that is AB as a segment. This explains why there is only 1 way for a 5-point, and 2 for a 7-point, but does not explain the 6-point. Of those remaining points (dealing only with the first half, again, mirror images), those that are factors of the number of total points do not work, because you will end up back at the starting point before hitting every number. AC is a factor in six because it passes point B, so it's 2. AD is a factor of 3 (B, C and D). Not only factors, but multiples of factors, as well (for example, skipping 4 points in the 6-point still does not work).
Using the knowledge of mirrors, first point impossibility (AB) and factors, we see that the number 1000 is made up of 10^3, or 2^3 5^3. Without going through every factor, it's quickly and easily discernible that of the numbers 1-1000, 2 or multiples of it encompass 500 numbers, all evens. Any multiple of 5 includes 200 numbers, half of which end in 0 and are already included with the 2's, so there are 600 unique factors and multiples between 1 and 1000. That leaves us with 400 that are *not , which should explain how many unique stars we can make. Remember to cut it in half because of mirroring, leaving us with 200, and to discount the AB segment (factor of 1), leaving us with 199. (If you discount AB, and THEN halve it, remember you needed to remove A[Z], the mirror image of that point).
guys someone copied this problem and you copied the answer. http://www.braingle.com/brainteasers/teaser.php?op=2&id=32838&comm=0
Log in to reply
lol
That someone is him obviously :P
can't understand "to discount the AB segment (factor of 1)". please help
nice. im very near my answer is 200.
Log in to reply
You forgot to subtract the 1000-gon. See below
Log in to reply
You solved this one also? @Satvik Golechha
Log in to reply
@Krishna Ar – Well....I had seen the problem 2 years before on some website......since then the answer was living in my eidetic memory.....
We enumerate the vertexs 1, 2, ..., 1000. Let's stay that the segment 1-2 has "distance" 1, the segment 1-3 has "distance" 2, the segment 1-4 has "distance 3", and so, the segment a-b has "distance" mín{b - a modulo 1000, a - b modulo 1000}.
The star where every segment has distance k and the star where every segment has distance 1000-k are the same, so there are only 500 valid distances for a star's segment. If star's segment distance isn't coprime with 500, then that "star" is not a star, so we have to exclude all the cases where that aren't coprime with 500 = 2^2 * 5^3, which is all the multiples of 2 and 5 between 2 and 500. So the possible distances are numbers finished in 1, 3, 7 or 9, which gives us 200 cases. But distance has to be greater than 1, and that lets 199 cases.
Solution: 199 cases.
We must "skip" the same number of vertices each time we connect a segment. If the amount we skip by divides 1 0 0 0 , then we will have the star only reach some fraction of the points, thus we find the number of integers which are coprime to 1 0 0 0 . This is equal to ϕ ( 1 0 0 0 ) = 1 0 0 0 ( 1 − 2 1 ) ( 1 − 5 1 ) = 4 0 0
However, realize that skipping by 1 (as well as by 9 9 9 ) would create a regular 1 0 0 0 sided polygon, which is not star. This gives 3 9 8
Furthermore, notice that skipping by an amount of n is equivalent to 1 0 0 0 − n , so we divide by 2 to get 1 9 9 .
Here we have to cover all the points of the star and move our pencil by leaving constant number of points every time. We cant repeat the points and have to come back to the starting point only after going through all the other points. If we have n points then we have to cover all { 0,1,2,3,...,n-1} points by doing (1+c*i)mod n where c= (1 + number of points to be left) and i increments from 0 every time by 1. Now to cover all the points it can b easily found that c has to be coprime with n . Now for every constant number, there is another constant number of points which forms mirror image of what we draw. So we divide the number of coprimes by 2. But as we have to leave non zero points so finally we subtract 1 from the answer.
First give names to all points(0,1,2,...,n-1).
If we have to construct star it means we can't connect 0 with 1 and n-1.
remaining points count = n-3 which can be connected with 0.
lets have an example for 8 points.
point gap 0 1 2 3 4 5 6 7
1 2 4 6 0
2 3 6 1 4 7 2 5 0
3 4 0
4 5 2 7 4 1 6 3 0
5 6 4 2 0
6 we can not cross 6 points(0 will join to 7)
We can cross only 1 to n-3 points on which some will repeat points and others will not.
we have n-3 possible sequences by adding (2,3,4,...,n-2) from our start point 0.
To create complete star we should not come to 0 again with out traversing all points.
here comes a little math to check, does sequence make a star or not?
if we add k each time for a sequence, our sequence will be-
* b+k mod(n) , b+2 k mod(n) , b+3 k mod(n) ,......, b+(n-1) k mod n [here b=0 start point] **
* k , 2k , 3k , 4k ,......, (n-1) k mod(n). **
none of these points should be zero.
suppose \gcd(k,n) = p(>1)
k = x*p;
n = y*p;
so y*k = (y*x*p) would be divisible by n and 1< y < n-1 because (p > 1).
so count sequences for which \gcd(k,n) should be 1. (2<=k<=n-2)
for n=1000 =>(2<=k<=998) => sequences = 348
and each star is counted twice (clockwise and anticlockwise)
Note: 0 to Z and 0 to (n-Z) would make the same star.
First, we notice that since the star has to "close", the amount of points skipped ( n ) times the number of lines in the star must be a multiple of 1000. Since the star doesn't go twice or more around itself, we have that the number of lines equals the L C M ( n , 1 0 0 0 ) / n . Since we want there to be exactly 1000 lines (so that all points are included in the star), we have that L C M ( n , 1 0 0 0 ) / n = 1 0 0 0 ⇒ L C M ( n , 1 0 0 0 ) = 1 0 0 0 n . Thus n and 1000 are coprime. We also have that 1 < n < 5 0 1 . In this range there are 250 even numbers, 100 numbers that are multiples of 5 and 50 numbers that are multiples of 10. Thus the number of 1000 pointed stars is 5 0 0 − 2 + 1 − 2 5 0 − 1 0 0 + 5 0 = 1 9 9
I looked at this as looking for an additive generator of a group containing 1-1000. To be a generator an element needs to be coprime with 1000. To avoid problems with symmetry(I.e. Going backwards being the same as going forwards), we will only consider numbers 1-500. 1000=10^3=5^3*2^3. So we need to eliminate the 250 even numbers. Then we need to eliminate the 100 multiples of five. Doing this will eliminate the 50 multiples of 10 twice, so we will add 50 so as to avoid double Counting. So there are 500-250-100+50=200 numbers less than 500 coprime with 2 and 5. We also cannot include 1 since that will make a polygon, and is not coprime with 1000, so there are 199 possibilities.
I wrote a simple python program to arrive at the answer. Assume the number of points in the star to be an array filled with zeros. Then iterate from integers 2 to half the number of points. For each of these iterations check if the array gets completely filled with zeros. If it does then its a valid STAR, else its invalid and you move on to the next iteration.
why? for evens there are no ways... like for six
It's just number theory: 2 φ ( 1 0 0 0 ) − 2 = 1 9 9 . where φ ( n ) is the Euler function, i.e., the number of integers between 1 and n coprime with n . We substract 2 because it must be a star (not a polygon) and then divide by two to avoid counting some configuration twice because of symmetry.