This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
I have come here via the related facebook post. The question is different there, the exponent there is on the outside - making (1) be the right answer. It is very confusing - I hope, someone will check it.
Log in to reply
Same here. I pin pointed graph 1 as the answer on facebook, came here, and instantly clicked on the first option. But to my surprise, the answer was different. Then I realized the question here was different. They should definitely correct this.
i made the same mistake here.. i checked only that and it confused me up
Log in to reply
It's just different question. Pay attention to detail. I've seen both and got them both correct, because I payed attention. The question shouldn't be changed because you saw it written differently somewhere else. That's asinine.
Log in to reply
@King De Jesús – Well... I have to disagree. Maybe I've misunderstood you or you have misunderstood us, but in my opinion this question should be the same as the related facebook question, especially, because they are connected via hyperlink. Edit: I have just checked and it has been corrected on facebook. :)
Yeah, the problem on facebook was just different from this site
The given expression is same as |x|. That's why it is always above the x-axis.
AGHHHHHHH, calculated it then went and looked at my denominators and not my answers and found -x to 0 to +x, darn that quick response LOL
Log in to reply
I fell foul yet again of the fact the question was different between the Facebook post and the actual site. I didn't re-read before selecting my answer.
The easiest way to answer this question is to analyze the domain of the function. Since the only potential restriction for even index radicals is that they can't contain negative numbers, and x^2 is always positive or equal to 0, this means that x can take on any real value for this function. This rules out options one and two, for sure. Since x^2 is positive or 0, and f(x)=sqrt(x^2), f(x) is also positive or 0. Therefore, the only picture that would make any sense is 3 (abs(x)).
Moderator note:
Good way of eliminating options.
contradicting your point "since x^2 is greater than 0 then f(x) has to be positive", take the example of x^2= 25, then f(x) can be equal to +/- 5 both. Therefore the answer should be y=+ or - X. If we are concerned only about the positive square root then y=|x| will hold good, but that isnt mentioned in the question
Log in to reply
I don't see any contradiction. f(x) = sqrt(x^2). If x = +/-5, then f(x) = sqrt((-5)^2) = 5, which is positive.
I agree! The correct answer should show an X because there are two solutions for every square root. The square root of 25 is +/-5.
Log in to reply
The square root of 25, denoted as 2 5 is just 5.
If we wanted to solve x 2 = 2 5 , we say that the answer is ± 2 5 , and not just 2 5 .
f ( x ) = x 2 ⇒ f ( x ) = ∣ x ∣ . ∴ the graph of f ( x ) is same as that of ∣ x ∣ . Hence 3 is the correct solution.
3 is the option because it is equal to y=abs(x) so it is in the first and second quadrant.
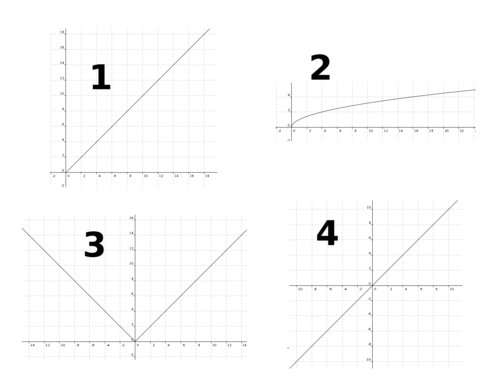
As we know x 2 = ∣ x ∣ . Thus the graph of y = ∣ x ∣ is the graph #3. □