A conversation at the Brilliant water cooler

Suyeon is thinking of 2 (not necessarily distinct) positive integers, x and y , each of which is greater than 1. She tells Calvin the product P = x y and Aaron the sum S = x + y . The equally intelligent Calvin and Aaron then engage in a short discussion as follows:
-
Calvin: "I cannot determine S at this point."
-
Aaron: "All right then, here's a hint; S does not exceed 2 0 , and if that's all you need to know to uniquely determine S then I will know what P is."
-
Calvin: "O.k., based solely on the fact that S does not exceed 2 0 I am now able to uniquely determine S ."
Find S + P .
This question was inspired by the long-suffering Calvin Lin (inside joke).
The answer is 79.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
This is simply an amazing problem.
There are many problems like this one online about two people having a conversation where seemingly, at first glance, no information is given and the problem is unsolvable. But upon closer inspection, there is just enough info to solve the problem. Every problem of this sort is unique in its own little way. This is without a doubt one of the most interesting ones that I've come across. Despite the fact that there is a little bash (which is shortened the more logic you use), it was definitely worth the time that I took to solve it.
Everyone knows how hard it is to solve these problems. But Most people take for granted how hard it is to make a problem like this. You first need an inspiration, then set conditions, then minimize the information given, then prove that it will work. And the worst part is: sometimes, the problem turns out in a way that there is no solution that meets the statements you gave, and when you make even the slightest change, you have to entirely reprove the statement. The chances of this happening can be minimized, but that almost always means making the problem easier. But you obviously didn't take the easy way out.
I'm curious as to how you did this problem, how did you guarantee that the answer was unique? Did you check every individual case or use a computer software? And how did you come up with the specific parameters, how did you know "is the info enough, or is there too much, or is it just right"
Log in to reply
Thanks for the appreciation, Trevor. This question has without a doubt taken more time to create and refine than any other question I've posted. @Calvin Lin posted a problem along these lines several days ago which I wrote a solution for and thought that was that. Then Pranjal Jain noticed that the solution was not in fact unique, so then I suggested to Calvin how to change the parameters so that the solution was unique. He made the change, I edited my solution and again thought that was that. Then, a few hours later it dawned on me that the solution was still not unique, at which point Calvin basically sighed and suggested that I post my own version. (This is why I refer to Calvin as "long-suffering".) You've summarized perfectly the frustration of this process in your second (main) paragraph.
So in the pursuit of creating my problem so that a unique solution could result from an exchange of as little information as possible I found I had to keep increasing the maximum value for S from what Calvin's problem had specified so that the filtering process would yield a unique solution. There was a fair amount of paper used, I assure you. The question was well-received after posting, but I still had a niggling doubt about the wording, and sure enough, Dylan and Adit pointed out the subtle error in what I had Aaron say initially. So then I had to figure out how to get around this, and eventually came up with Aaron's present conditional statement. The previous wording had Calvin as the star of the show, but now it turns out Aaron had to be the pivotal character in this drama.
I think that you're the first to solve the problem since the change in wording, so it's great to hear your positive feedback. As you say, I could have taken the easy way out at several occasions in the process, but I'm glad now that I stuck with it. Hopefully Dylan and Adit will approve of the wording now as well.
Thanks for giving me the opportunity to describe the process of creating this problem; it was quite therapeutic.
P.S.. I gather the AMC exams are this month, (and that you may already have written one). Hope they go well. :)
Log in to reply
I am officially a fan. I enjoyed reading about the process of making this problem almost as much as solving it. Unfortunately, I did not notice that there were multiple products that have the same sum of factors less than 21. I actually made it as far as listing them out exactly as you did but I was left confused why they couldn't all be the answer. The reason why not is the most elegant masterstroke ever, It seems too good to have been devised by a human :P Did you plan it that way or was it a happy accident?
Haha, "therapeutic"
The AMC unfortunately didn't go so well. But then again, it didn't go well for anyone. Everyone that I talked to thought that this year's AMC 10 was unusually hard.
I got somewhere between 110 and 118.5, but you need a 120+ to qualify. However, if < 2 . 5 % of people score > 1 2 0 , then they'll take the top 2.5% of scores. If this doesn't happen, then I'll just take the 10B. Or even if I make it I may still take the 10B just so I can miss school :P.
Btw, could you link the original problem (Calvin's) to this problem, unless it's been deleted.
Log in to reply
@Trevor Arashiro – Well, if everyone found it unusually difficult then it would seem likely that the floor of 120 will be lowered. I was wondering what the A and B were; so even if you don't need to take the B you'll take it anyway just to get out of school? Yeah, that's not nerdy at all. :D
Calvin catapulted the original problem into oblivion after I posted my problem, so sorry, no link. :( Anyway, in brief, the conversation he presented was different and the sum ceiling lower compared to my version, and yet it could not be fixed without either a restructuring or the exchange of more information, which was what prompted my fascination. My initial reaction to his question was that it would be quite straightforward. Was I ever wrong about that. :P
P.S.. Were you the moderator who modified my response to your original comment? :) As far as I can tell only an @ was deleted. I ask partly for fun, but also to check whether the formatting had gone haywire; I've been having trouble with the site editor today, (the cursor keeps playing peek-a-boo and the occasional random symbol appears out of nowhere). If it continues messing up tomorrow I'll notify Calvin.
This is by far one of the most interesting questions I have ever done. You don't need to know any special theorems, though the AM-GM helps to narrow down choices a lot. Even without it, you can still do the question: you'll just keep on doing until you realize the larger numbers can never have factors that sum up to 20. The rest is just, well, logic.
Well done for coming up with such a great problem.
Log in to reply
Sometimes, you just have to wonder how he makes these problems.
Thanks! I'm glad that you enjoyed the problem. :)
I am uncomfortable with the statement "Now if Aaron knew that Calvin could not initially determine S , then S must be expressible as the sum of a prime and a composite number or of two composite numbers. " I believe it should instead be S should not be expressible as the sum of of two primes .
for example say S=15; x and y could be 13 and 2 hence P would be 26 in case of which Calvin would be able to identify S. Hence Aaron could not confidently say that Calvin cannot determine S
Log in to reply
You're right; thanks for pointing out my mistake. I've proposed a remedy in my comment to Dylan, and will edit my solution in acknowledgement of your concerns. :)
Suppose Aaron receives the information that S = 1 6 . How would Aaron know with absolute certainty that Calvin would definitely not be able to determine S ? Calvin may have received the value P = 3 9 and deduce immediately that { x , y } = { 3 , 1 3 } and S = 1 6 .
Have I misread the problem?
Log in to reply
Yes, you and Adit have essentially made the same accurate point. My proposed remedy is to just have Aaron say, "Here's a hint: S does not exceed 2 0 , and if that's all you need to know. to uniquely determine S then I will know what P is". Does that sound reasonable to you? Thanks for pointing out the mistake. :)
P.S.. I apologize if the wording of the question prevented you from getting the "correct" answer. I still believe that 6 3 + 1 6 = 7 9 is the solution, but Aaron definitely misspoke in my pre-edited version of the conversation. :(
why isn't x = y = 1 0 accepted?
Log in to reply
That would be because products of 7 5 and 9 6 would also lead to a minimum singular sum of 2 0 , which would mean that Calvin would not have been able to assure Aaron that he would know what x and y were as well. Only a product of 6 3 leads to a unique singular sum under 2 1 , namely 1 6 .
Log in to reply
oh... i get it...
Log in to reply
@Julian Poon – Great. The logic in this question is a bit tricky and it took me a long time to be comfortable with my solution, but the more people that get it the more comfortable I become in the belief that my logic is valid. :)
What about 9 and 9
This solution is a visual representation of Brian’s approach. We further improve on it by drawing the matrix who rows are the sums S, columns are the product P, and the entry is colored if there are integers x , y , > 1 such that x + y = S , x y = P .
This is an infinite table, so let’s not reproduce it as yet. Setting up this table requires a lot of tedious work (which Brian mentioned). Here are the first 10 rows, to give you an idea of what is happening

For example,
x
=
2
,
y
=
2
gives us
S
=
4
,
P
=
4
so the cell
(
4
,
4
)
is marked.
Similarly,
x
=
2
,
y
=
3
gives us
S
=
5
,
P
=
6
so the cell
(
5
,
6
)
is marked.
We are not allowed to use
x
=
1
,
y
=
4
, so the cell
(
1
+
4
,
1
×
4
)
is not marked.
We will aim to remove rows and columns whenever we can. Once a row or column has no marked squares in it, this indicates that there are no valid solutions, and so we can delete them. EG we can remove the first 3 rows.
Now, let’s start the analysis. Calvin says “I cannot determine S at this point”.
If a number has 2 factors, of the form
1
,
p
, then there is no
x
,
y
>
1
.
If a number has 3 factors, of the form
1
,
p
,
p
2
, then there is no
x
,
y
>
1
.
If a number has 4 factors, of the form
1
,
p
,
q
,
p
q
, then there is only 1 set of
x
,
y
>
1
, and so Calvin can determine S.
If a number has 4 factors of the form
1
,
p
,
p
2
,
p
3
, then there is only 1 set of
x
,
y
>
1
, and so Calvin can determine S.
Conversely, if a number has 5 or more factors, then there are 2 distinct ways to express the product, and hence Calvin cannot determine S.
Thus, we can eliminate numbers with 4 or fewer factors, while keeping the rest of the rows. (We still have an infinite table, so I'm not reproducing it here.)
Arron says “S does not exceed 20”, which means that we can get rid of columns without any entries in the top 20 rows. This gives us
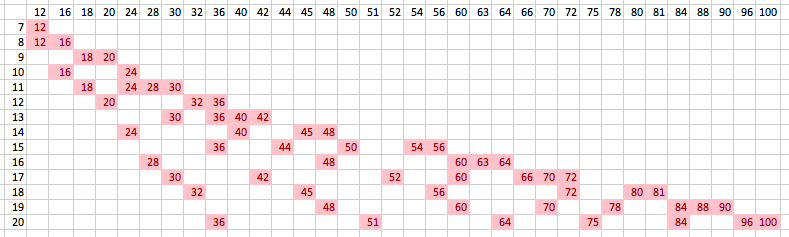
Since all Calvin needs to know is the value of S to uniquely determine these numbers, this means that we’re looking for columns with exactly 1 entry. Thus, we can delete the following yellow columns
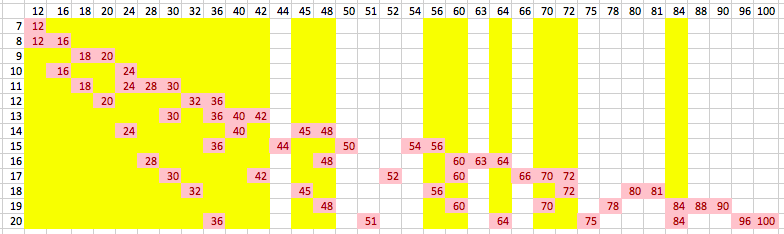 After deleting these columns, we can delete empty rows to get:
After deleting these columns, we can delete empty rows to get:
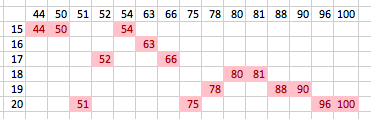
Now, Arron’s comment about “then I will know what P is” means that there is a unique number in the row that we're interested in. Thus, we can get rid of the following rows to obtain:
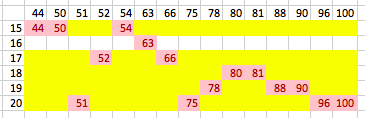
Hence, the only possibility is S = 1 6 , P = 6 3 .
@Brian Charlesworth This solution, while essentially equivalent to yours, makes the following improvements:
- Organizing the data according to ( S , P ) , to make it easier to consider what happens for a particular S or P value.
- Calculating valid ( S , P ) pairs beforehand, which makes it easier to find possible pairs given a particular S or P value, as opposed to "Given a particular S (or P ) value, to find all other valid pairs".
Log in to reply
I really like this approach to testing possible (x,y) pairs. I used lists and found it cumbersome. Being a retired teacher I'm good at "tedious" jobs like marking exams so I went ahead and took my ordered pairs through this process. The row with Sum=16 should have THREE possible PRODUCTS: P=63 for (7,9) and P=55 for (5,11) and P=39 for (3,13). I don't think the answer provided is correct because if you eliminate a row or column too early - you miss possible pairs. Brian's list is missing key entries as well - making his conclusion suspect. Congratulations on creating such a fun learning experience !
Log in to reply
I'm glad that you enjoyed the question. :) Since both x and y exceed 1 , if Calvin knew that P = 5 5 = 5 ∗ 1 1 then he would know that S = 5 + 1 1 = 1 6 right away, and if he knew that P = 3 9 = 3 ∗ 1 3 then he would know that S = 3 + 1 3 = 1 6 right away. So since he is not able to immediately determine S we know that P is neither 5 5 nor 3 9 .
If P = 6 3 = 3 2 ∗ 7 then S could be either 3 + 2 1 = 2 4 or 9 + 7 = 1 6 , so this number survives the "cut" after Calvin's first statement.
Log in to reply
@Brian Charlesworth – Got it !! Thanks Brian. I missed eliminating those two columns for having a product that was a factorization into two primes. I caught many others where (x,y) was (2,2),(2,3),(2,5)(2,7),(2,11),(3,5) etc. Just missed P=55 & P=39. Nice problem !!! How long did it take you to refine it ?
Log in to reply
@Bob Kadylo – It took several hours over a period of a couple of days to refine it to its present form. On several occasions I thought I had it just right only to discover another flaw, (or have one pointed out to me), so while it was a somewhat frustrating process, I'm glad I stuck with it. :)
Terrific! :D This does streamline the process, and should really help readers understand the "tedious work" I referred to but did not expand on sufficiently.
Wow. This solution is easy to understand!
Just a small correction: If a number has 3 factors, of the form 1 , p , q
Log in to reply
Thanks. I've edited it. The 3 factors are of the form [ 1 , p , p 2 . Read number of factors to understand how to count these / determine the form that they are.
Why can't x and y be 10? Calvin would know P = 100 but obviously there would be multiple ways of having that as a product. If S can't exceed 20 then 10 and 10 is the only viable option.
Log in to reply
Well, work out that logic further, and use the above process to help you understand what is happening and when. Observe that (20, 96) is another entry in the row that led to removal of the cell (20, 100).
Calvin knows P = 100, Aaron knows S = 20.
Calvin cannot determine S at this point.
Aaron tells Calvin that S does not exceed 20, and Calvin knows what the numbers are.
Given that Calvin knows what the numbers are, how does Aaron know what the numbers are? For example, Arron doesn't know that the product cannot be 96. If the product was indeed 96, and the sum does not exceed 20, then Calvin could also figure out what the numbers are.
a little misunderstanding i have about this problem and solution... i would kindly ask you to explain why such a pair of numbers as (15, 5) is NOT the solution to the problem? unfortunately, i fail to see the reason here.... - it seems to have a sum not bigger than 20 - one of the numbers (15) isn't prime... - the product of these numbers is 75, which can be achieved in two ways: 25 3 and 15 5 (as long as the divisors of 75 are 5, 5 and 3);
i admit there may be "an elephant in the room" which i'm still struggling to notice:)))
Log in to reply
From Aaron's perspective, Calvin being able to determine S must result in Aaron being able to uniquely determine P . But in the case of ( x , y ) = ( 5 , 1 5 ) , while Calvin, knowing that P = 7 5 , will be able to determine that S = 2 0 , Aaron will not be able to uniquely determine P , for from his perspective P could still also be 9 6 = 8 × 1 2 . That is, if P had been 9 6 then Calvin could have determined that S = 2 0 given the same hint, but then Aaron would have no way of knowing whether P was 7 5 or 9 6 .
I can understand the "struggle"; no spoken language is "mathematical" in nature, so it was difficult to phrase this problem in a way that would clearly match it's logical intention. It was the best I could come up with, and after reading the previous paragraph I hope that you are able to see how my problem can be read in the way that I intended.
Log in to reply
i'm very grateful for the explanation you gave! i think it helped me to figure out my misjudgement and i seem to have caught that very same elephant in the room i was talking about before!
and to clear my doubts would you agree with me on the following: were it "S is less than 20" (rather than "doesn't exceed 20"), there would be (at least) two solutions the the problem in this case, which are (7,9) and (8,8)?
Log in to reply
@Nik Gibson – Yes, that's correct. I required S ≤ 2 0 in my problem so that the ( 8 , 8 ) possibility could be eliminated, since for both 8 × 8 = 6 4 and 4 × 1 6 = 6 4 we have S ≤ 2 0 . If we required that S < 2 0 then the 4 × 1 6 option would no longer apply, leaving ( 8 , 8 ) as a possible solution along with ( 7 , 9 ) , which in turn would have meant that the question no longer yielded a unique solution. It took quite some time to make sure this question "worked" properly; I'm glad you enjoyed it. :)
Log in to reply
@Brian Charlesworth – :)) i might have some tiny thing to advise you on the puzzle text: what would you say about Calvin replying "if you're saying S is not bigger than 20, then i'm able to determine it uniquely" (instead of just "I am now able to uniquely determine S")?
i mean these two statements are a bit different! if the very fact of "S isn't bigger than 20" helps Calvin to determine this very S, then it should be said so directly... the way it is said now implies slightly different thing, namely: Calvin is able to determine S not just because S<20, but ALSO because Aaron can determine P, as he said in his conversational turn...
Do you agree?
Log in to reply
@Nik Gibson – Ah, o.k., I see your point. The difference is subtle, and I don't think any other solutions would be introduced if Calvin were to give weight to the fact that Aaron can determine P if his hint helps Calvin, but for sake of linguistic precision I will make the edit. (This will also more closely align with the reasoning used in the two posted solutions.) Thanks for helping refine the question. :)
Log in to reply
@Brian Charlesworth – I agree that "any other solutions would be introduced if Calvin were to give weight to the fact that Aaron can determine P if his hint helps Calvin", but there will be only one way of interpreting Calvin's words:)) thanks for your attention!
First, since both x and y exceed 1 their product P cannot be prime. Now if both x and y were prime then Calvin would know what the two numbers were, (and hence also their sum), as a result of knowing P . For example, if P = 1 0 then the two numbers could only be 2 and 5 , giving S = 7 . Thus at least one of x , y is a composite number, and so the prime decomposition of P must meet one of the following forms:
(i) p 1 a 1 ∗ p 2 a 2 ∗ . . . ∗ p k a k for primes p n with k ≥ 3 and each a j ≥ 1 ,
(ii) p 1 a 1 ∗ p 2 a 2 , where a 1 , a 2 are positive integers at least one of which exceeds 1 , or
(iii) p k for k ≥ 4 .
Now by the A.M.-G.M. inequality, we know that ( x + y ) ≥ 2 x y . So if ( x + y ) ≤ 2 0 , as Aaron has stated in his hint, we know that x y ≤ 1 0 ⟹ x y ≤ 1 0 0 .
Now that, given Aaron's assurance, Calvin has enough information to determine x and y , we know that P is such that, of the possible sums, only one is strictly less than 2 1 . For example, If P had been, say, 6 6 , then since 6 6 = 2 ∗ 3 3 = 3 ∗ 2 2 = 6 ∗ 1 1 the possible sums that Calvin could have originally guessed at would have been 3 5 , 2 5 and 1 7 . Once he was told that S did not exceed 2 0 he could then determine that S = 1 7 and thus that x and y were 6 and 1 1 . But from Aaron's perspective, in this case it would not be enough to know that Calvin has determined the two numbers, since, for example, 5 2 = 2 ∗ 2 6 = 4 ∗ 1 3 would have a unique sum of 1 7 under 2 1 as well. So we need to find a product P that has a single potential sum under 2 1 that no other product ≤ 1 0 0 has as well.
Now comes the tedious work. We need to go through all the products ≤ 1 0 0 that meet one of the conditions (i), (ii) or (iii), find those that have a single potential sum under 2 1 and compare. Here is a list of the candidates in the form ( X , d ) where X is the product and d is the single sum strictly under 2 1 :
( 4 4 , 1 5 ) , ( 5 0 , 1 5 ) , ( 5 1 , 2 0 ) , ( 5 2 , 1 7 ) , ( 5 4 , 1 5 ) , ( 6 3 , 1 6 ) , ( 6 6 , 1 7 ) , ( 7 5 , 2 0 ) ,
( 7 8 , 1 9 ) , ( 8 0 , 1 8 ) , ( 8 1 , 1 8 ) , ( 8 8 , 1 9 ) , ( 9 0 , 1 9 ) , ( 9 6 , 2 0 ) , ( 1 0 0 , 2 0 ) .
All the sums are duplicated except in the case ( 6 3 , 1 6 ) . So since 1 6 is the only possible unique solution given the information provided by Aaron, Calvin can conclude that S = 1 6 , and once he states that he has determined S Aaron can then conclude that P = 6 3 .
Thus S + P = 1 6 + 6 3 = 7 9 .