A cool-aboration Problem
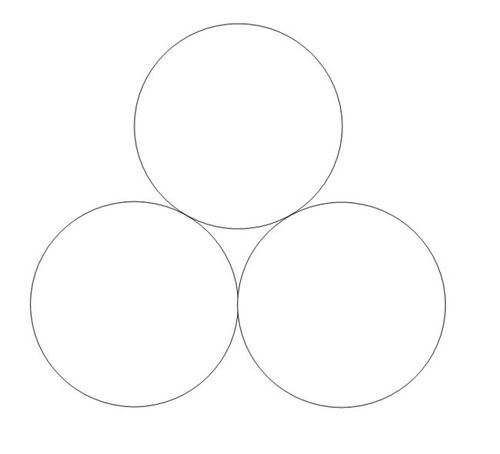 Figure above shows 3 circles each with radius of 1 touching the other two circles externally.
Figure above shows 3 circles each with radius of 1 touching the other two circles externally.
Find the area bounded by the three circles. Give your answer to 3 decimal places.
Use the approximation π = 7 2 2 .
This Problem is created By Me and Nihar Mahajan . We Hope you like it!
The answer is 0.161.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Upvoted. That yellow part is unreadable though.You might wanna change that.
Since Mehul has not elaborated properly.Let me post a nice solution :
Construct a triangle by joining the centres of the 3 circles.Indeed this triangle will have all its sides of length 2 r = 2 and thus is an equilateral triangle.
Thus area of an equilateral triangle = 4 3 ( s i d e ) 2 = 4 3 ( 2 ) 2 = 3
We can see that 3 congruent sectors are formed.Since there is an equilateral triangle , each angle of these sectors : θ = 6 0 0
Area of 3 sectors = 3 × 3 6 0 θ × π r 2 = 3 × 3 6 0 6 0 × ( 7 2 2 ) ( 1 2 ) = 7 1 1 .
Hence required area = 3 − 7 1 1 ≈ 0 . 1 6 1
Note: This question assumes that π = 7 2 2 .
Did the exact same
Construct a Equilateral triangle by Joining The Centers of the circles.The triangle is equilateral because all the sides of the triangle are of the same length.The triangle will have a side of two units.
The area of the triangle is 4 3 ∗ 2 ∗ 2 = 3 square units.
Now, We subtract The area of the Three sectors of the three circles.
= 3 ∗ 7 2 2 ∗ 1 ∗ 1 ∗ 6 0 ∗ 3 6 0 1 = 7 1 1 u n i t s .
Because Area of a sector Is P i ∗ r 2 ∗ θ ∗ 1 / 3 6 0 . Where theta is the angle of the sector at the center. r is the radius of the circle. And since we have 3 sectors, we multiply by three.
Hence, The area enclosed is 3 − 7 1 1 which is Approximately 0.161 square units.
And, We are done.
Cheers!
Thanks for posting it and mentioning me. Cheers!
Challenge Student Note: It is correct.But phrasing of the construction is ambiguous.What do you mean by 'Joining The "radii" of the circles'? It must be 'Joining The "centres" of the circles'.
Nice problem.Just wanted to state out some typos.First off as Nihar Mahajan Already said,"by joining the centers of the circles" we can get the equilateral triangle and also you need to prove that the triangle is in fact equilateral.
I'm really sorry for being a spelling-nazi but I'm just trying to help:
-
The triangle "Will Have"(Caps? why?) a ...
-
Now, We(?) subtract The(?) area of the Three(?) sectors.
-
... is Approximately(?) 0.161 (s)"quare" units.
-
We(?) are done.
Again I'm sorry if you got me wrong I'm just trying to make it better. Cheers!!
Log in to reply
I'm Sorry. Adding Caps is sort of my Habit :P. For the rest, I think that This is the type of Language used While typing the solution. Saying 'we'. Rest of the typos, I have fixed. Thanks! :)
Log in to reply
Please try and break the habit of randomly adding capital letters to your sentences. It makes it much harder to read, as it breaks up the expected continuity of small letters.
@Calvin Lin sir, I have Cleaned the solution up. Kindly see to it. :D
Log in to reply
@Mehul Arora , I have also added a diagram to my solution so that the reader can understand what you are trying to tell.
Cheers! XD
the figure formed is a curvalinear triangle with a formula generated by FOX is 0.161r^2 since r = 1 then area = 0.161
The figure shows 3 lines connecting the centres of the 3 circles to form a triangle.
The answer to this question is the area of the o r a n g e region in the middle.
The angles of the triangle are 60 degrees each because it is an equilateral triangle and each side is 2 units.
So the y e l l o w areas are 3 sectors with angle 60 degrees and radius 1.
A r e a = 3 6 0 θ π r 2 = 3 6 0 6 0 π = 6 π
So area of 3 sectors is 3 × 6 π = 2 π
Now we know the area of y e l l o w region. We can subtract it from the area of the equilateral triangle of side length 2.
A r e a o f e q . t r i a n g l e = 4 3 a 2 = 4 3 ( 2 2 ) = 3
So our answer is 3 − 2 π ≈ 0 . 1 6 1
Please upvote if you liked the solution.