A Family of Cubics
Let the general cubic polynomial with integer coefficients f ( x ) = a x 3 + b x 2 + c x + d have the trait that f ( 1 ) = 2 k for some integer k . Does there exist a k such that f ( x ) has the factor a x 2 + ( c − d ) x + d ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
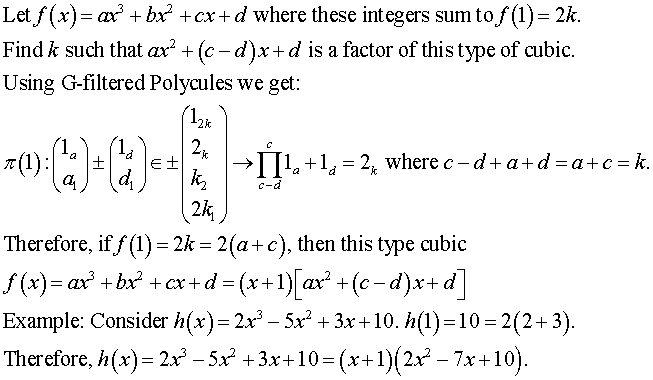
this facebook video explains the Game of G-filtered Polycules for Cubics; leave a comment.
What is G-filtered Polycules?
Log in to reply
it's a process I designed to rational factor a polynomial of any degree. I'm using it now to reverse engineer Math problems to see if there are any other processes out there to solve these problems. If you're on facebook I can invite you to the G-filtered Polycules group: https://www.facebook.com/groups/factorthis/
Log in to reply
That is not possible. By Galois Theory, we can show that not all polynomials of degree 5 or above can be expressed as algebraic numbers.
Log in to reply
@Pi Han Goh – G-filtered Polycules will reveal all rational factors of any polynomial if they exist. If none are found via G-fP then the polynomial has no rational factors (or rational roots). I'm gonna read about Galois Theory, Thanks !!! This facebook video explains the Game of G-filtered Polycules for Cubics; leave a comment: https://www.facebook.com/TruSpot/videos/vb.1021243805/10208395010805791/?type=2
Log in to reply
@Frank Giordano – Your algorithm is either wrong or unnecessarily complicated. A simple rational root theorem should do the trick.
Log in to reply
@Pi Han Goh – Well, the G-filter is called a filter because it filters out the Rational Root Theorem (RRT) 'roots' that are impossible. So you check every root revealed by the RRT in a 7th degree polynomial, and I'll use a G-filter, and we'll compare notes on which is "simpler" !o!
Log in to reply
@Frank Giordano – is this "filter" of yours rigorous? has this been peer -reviewed by other mathematicians?
Log in to reply
@Pi Han Goh – it can be taught to Junior High School graduates before they enter High School.
Log in to reply
@Frank Giordano – You didn't answer my question.
Log in to reply
@Pi Han Goh – i answered one of them lol
@Pi Han Goh – https://brilliant.org/problems/successive-cubic-rational-root/
@Pi Han Goh – how would you solve this problem: https://brilliant.org/problems/filtering-the-rational-root-theorem/?ref_id=1261522
Log in to reply
@Frank Giordano – Just apply intermediate value theorem .
Log in to reply
@Pi Han Goh – tough crowd lol. try this one: https://brilliant.org/problems/prime-cubic-root-2/
get the latest version of "G-filtered Polycules" here: https://www.facebook.com/groups/factorthis/
f ( x ) ⟹ f ( 1 ) 2 k = a x 3 + b x 2 + c x + d = a + b + c + d = a + b + c + d
If f ( x ) has the factor a x 2 + ( c − d ) x + d , we can assume:
f ( x ) = ( x − g ) ( a x 2 + ( c − d ) x + d ) = a x 3 + ( c − d − a g ) x 2 + ( d − c g + d g ) x − d g
Equating coefficients, from the constant term, we have g = − 1 ; and from the x 2 term,
b b + d a + b + c + d 2 k = c − d − a g = a + c = 2 a + 2 c = 2 ( a + c ) g = − 1
⟹ Yes, k = a + c