A fishy problem!

If $\theta$ is the angle of refraction of a light ray passing through the horizon and hitting the eye of the fish, then:

\(

sin(\frac{\pi}{2}) = \frac{4}{3} sin(\theta) \)

$sin(\theta) = \frac{3}{4}$

We know that:

$r = 12 \times tan(\theta)$

$r = 12 \times \frac{sin(\theta)}{cos(\theta)}$

By Pythagoras:

$r = 12 \times \frac{3}{4} \times \frac {\sqrt{144+r^{2}}}{12}$

$\frac{16}{9} \times r^{2} = 144 + r^{2}$

$\frac{7}{9} \times r^{2} = 144$

\( \boxed{r = \frac {36}{\sqrt{7}}}

\)

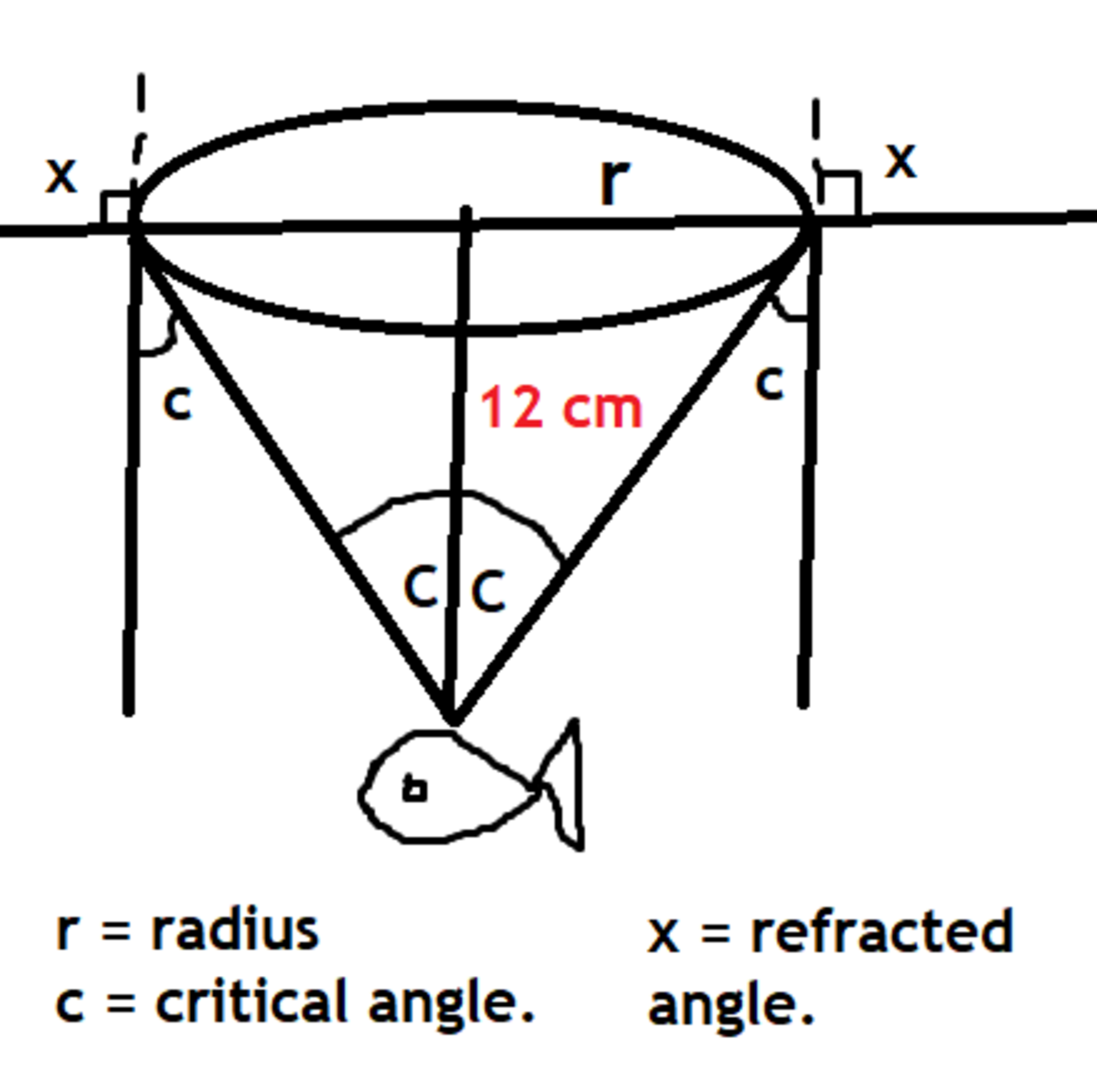
In the diagram above, the fish can see until the critical angle as the light would then reflect back in the water. Also, this works because to show what the fish sees we can trace the path of the light from the fish's eye to the outside world.

Now using Snell's law, $\frac{sin C}{sin x}$ = Refractive index. ( here r= 90 degrees, hence sin r = 1)

Therefore, sin C = $\frac{4}{3}$ and using some trigonometry we will find tan C = $\frac{3}{root7}$

Also, tan C = $\frac{r}{12}$ . Therefore r = 36/ root 7

If the refractive index of water be $n$ and the depth of the object (the fish) be $h$ below the free surface of water, then the radius asked is

$\dfrac{h}{\sqrt {n^2-1}}$

Here $n=\dfrac {4}{3},h=12$ . So the radius is

$\dfrac{12}{\sqrt {(\frac{4}{3})^2-1}}=\boxed {\dfrac {36}{\sqrt 7}}$ .