A geometric puzzle
The A B C triangle is right angled. We know that:
A C B ∠ = 9 0 °
B A C ∠ = 1 5 °
A B = 1 0 0
What is the area of the A B C triangle?
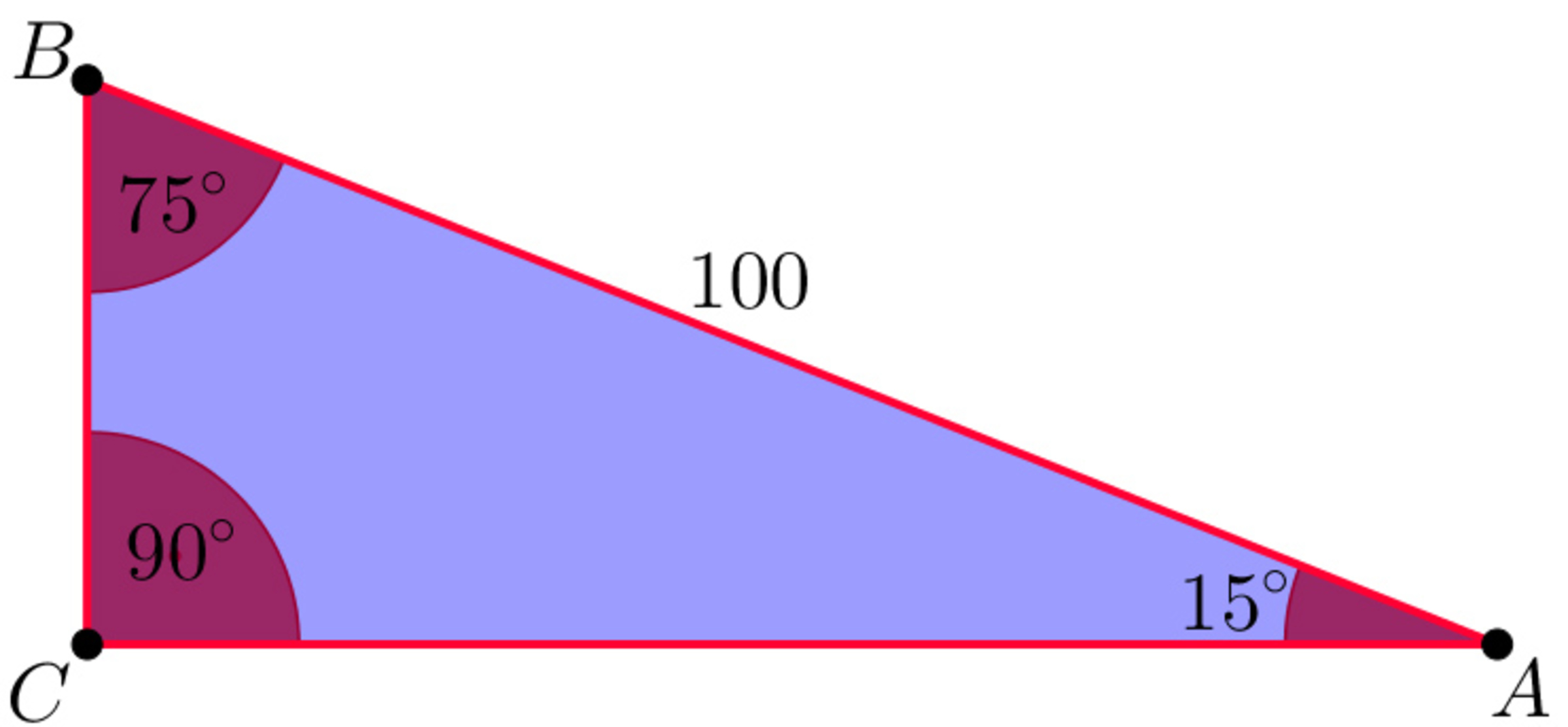
The answer is 1250.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
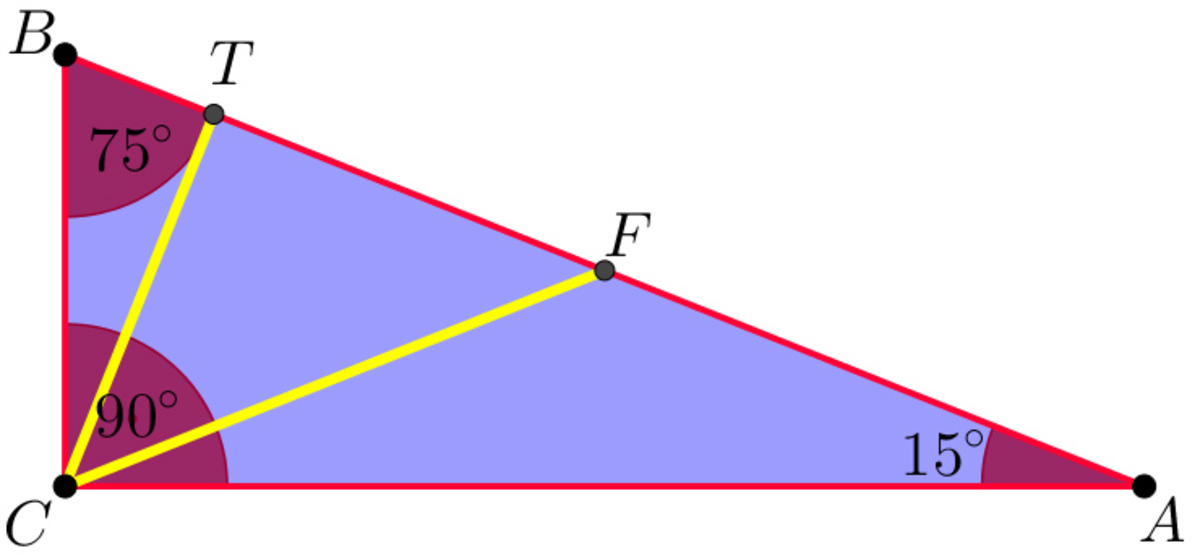 Let
F
be the midpoint of
A
B
, and
C
T
is an altitude of the triangle. From the Thales theorem
C
F
=
A
F
=
B
F
. From that
B
C
F
∠
=
7
5
°
and
B
F
C
∠
=
1
8
0
°
−
7
5
°
−
7
5
°
=
3
0
°
. So the
C
T
F
is a half-equilateral triangle. Then
C
T
=
2
C
F
. Now we can see that
C
T
=
2
C
F
=
2
A
F
2
2
A
B
, so
T
A
B
C
=
A
B
∗
C
T
/
2
=
1
0
0
∗
(
1
0
0
/
4
)
/
2
=
1
0
0
∗
2
5
/
2
=
1
2
5
0
.
Let
F
be the midpoint of
A
B
, and
C
T
is an altitude of the triangle. From the Thales theorem
C
F
=
A
F
=
B
F
. From that
B
C
F
∠
=
7
5
°
and
B
F
C
∠
=
1
8
0
°
−
7
5
°
−
7
5
°
=
3
0
°
. So the
C
T
F
is a half-equilateral triangle. Then
C
T
=
2
C
F
. Now we can see that
C
T
=
2
C
F
=
2
A
F
2
2
A
B
, so
T
A
B
C
=
A
B
∗
C
T
/
2
=
1
0
0
∗
(
1
0
0
/
4
)
/
2
=
1
0
0
∗
2
5
/
2
=
1
2
5
0
.
To be honest I find this a nice, but complicated solution to a pretty straightforward problem.
@Peter van der Linden - My geometry puzzles usually have a solution with trigonometry and a solution without it for younger students like me! At the moment I'm not so good in trigonometry, I'm going to learn about it two years later...
Log in to reply
Are you serious? You are 14 yrs and you didn't learn trigonometry ??!!
Log in to reply
Well now I'm learning it, but not in school!
We are going to find the area of the triangle by finding the lengths of the triangle: Let x denote the length of BC and y denote the length of AC.
S i n 1 5 = 1 0 0 x .................So.................. 1 0 0 S i n 1 5 = x = 2 5 6 − 2 5 2
S i n 7 5 = 1 0 0 y .................So.................. 1 0 0 S i n 7 5 = y = 2 5 6 + 2 5 2
Now we have found the lengths as:
x = 2 5 6 − 2 5 2 ..................and................... y = 2 5 6 + 2 5 2
Here we can go for an interesting approach using the fact that:
( a + b ) ( a − b ) = a 2 − b 2
( 2 5 6 ) 2 − ( 2 5 2 ) 2 = 2 5 0 0
and then we can simply divide it by 2 using the fact that 2 5 0 0 is equal to the length of the height into the length of the base
2 2 5 0 0 = 1 2 5 0
Since the triangle is right angled its area is:
( A B C ) = 2 1 ⋅ A C ⋅ B C
Also:
s i n B A C ∠ = A B B C ⇒ B C = s i n 1 5 ° ⋅ 1 0 0
c o s B A C ∠ = A B A C ⇒ A C = c o s 1 5 ° ⋅ 1 0 0
Therefor:
( A B C ) = 2 1 1 0 0 2 s i n 1 5 ° c o s 1 5 °
By using the trigonometric identity s i n 2 a = 2 s i n a ⋅ c o s a ⇒ s i n 1 5 ° ⋅ c o s 1 5 ° = 2 s i n 3 0 ° = 4 1
Hence:
( A B C ) = 8 1 1 0 0 2 ⇒
( A B C ) = 1 2 5 0