This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
Is it assumed that point O is the centre of the circle. Without that assumption I'm not sure the proof works.
Log in to reply
Indeed. I have added that clarification in.
How do we know that the triangles are similar?
Log in to reply
Thanks for the comments. I have explained it.
Log in to reply
I suggest you use the term 'congruent'.
Log in to reply
@William Nathanael Supriadi – Thanks. You are right. I was not sure of the meaning.
How do you make such kind of diagrms? What software?
Log in to reply
I copy the figure in the problem and paste in in Print and edit it.
The circle and the fact that O is the center are meaningless additions to make the problem appear tougher than it is. No Pythagoras calculations needed either. Just keep looking and logic alone reveals the answer.
Log in to reply
I disagree. We need that O F = O C , which follows from O being the center of the circle. If there is no restriction on O F , then the height can be any value (since it is equal to O F 2 − 5 2 .
Where did the last two equations come from?
Log in to reply
Pythagoras again
Log in to reply
Yes, that's right. Thanks.
Log in to reply
@Ahmad Saad – I think your first question on Brilliant
Log in to reply
@Vishwash Kumar Γξω – Yes. That's another options of previous problem belongs one of site members which Mr. Calvin ask for.
If we consider the lower triangle, we can form a 5-12-13 right triangle. Thus, the radius is 13. Now in the upper triangle, we can form another 5-12-13 triangle. Thus, h = 12.
I interpreted your diagram as h being the entire red line, which is AB, not just AO. So h to me was 12 + 5, but you did not list 17 as an answer. I should have left it blank. The problem was not well diagrammed.
(r-5)(r+5)=12×12 ............ r^2 - 25=144 ................... r =13 .............. From pythagorean theorem h^2=r^2-5^ Then h=12
The triangle DO and right angle = triangle OE and right angle. Therefore, h = 24/2 = 12.
The triangles E-O-1/2EF and D-O-1/2DC are equal as they both consist of sides 5 and a radius, therefore we have h given as 1/2 DC or 12.
5^2+12^2=5^2+h^2
I) OD = OC = OE = OF as radii of same circle.
II) According to Pythagoras theorem OD = 13, as OD^2 = (5)^2 + (24/2)^2
III) In triangle OEF, OE = OF = 13 and half of base = 5. Let 'A' be the mid-point of line EF i.e. base of triangle OEF. By applying Pythagoras theorem on triangle OAF will get OA i.e. h = 12.
Let us consider the mid point of DC be A and the mid point of EF be K Considering triangle OAC, we have (OC)^2 = (OA)^2 + (AC)^2 and we get OC=13. Since O is the centre of the circle, OC and OF are the radius and hence they are equal. Thus in triangle OKF, (OK)^2 = (OF)^2 + (KF)^2 And thus h = 12
Notices that there are 4 right triangles and they satisfy 5^2 +12^2=13^2. So, h=12.
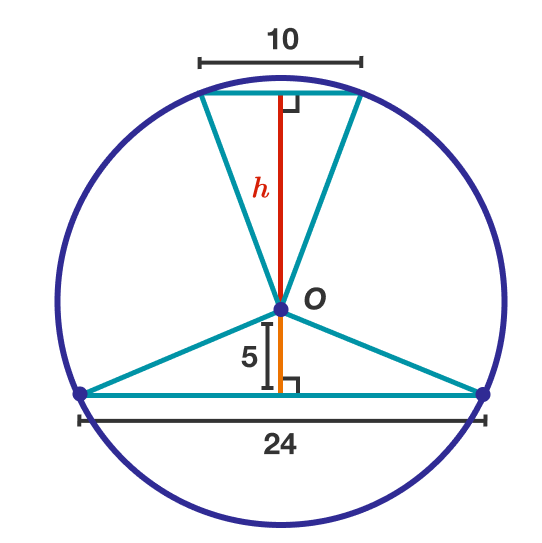
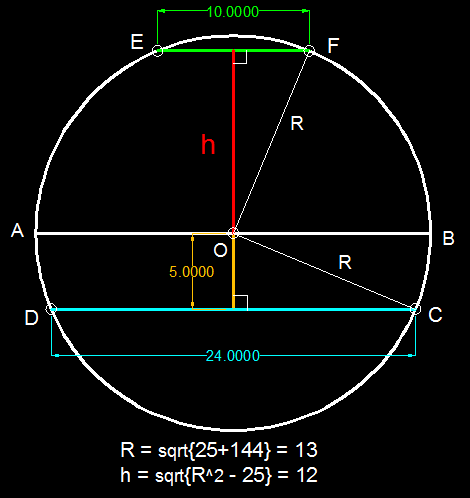
We note that A F = B O = 5 , O F = O C = r and ∠ O A F = ∠ C B O = 9 0 ∘ , therefore △ A O F and △ C B O are congruent. So A O = C B or h = 1 2 .