Lovely Kite
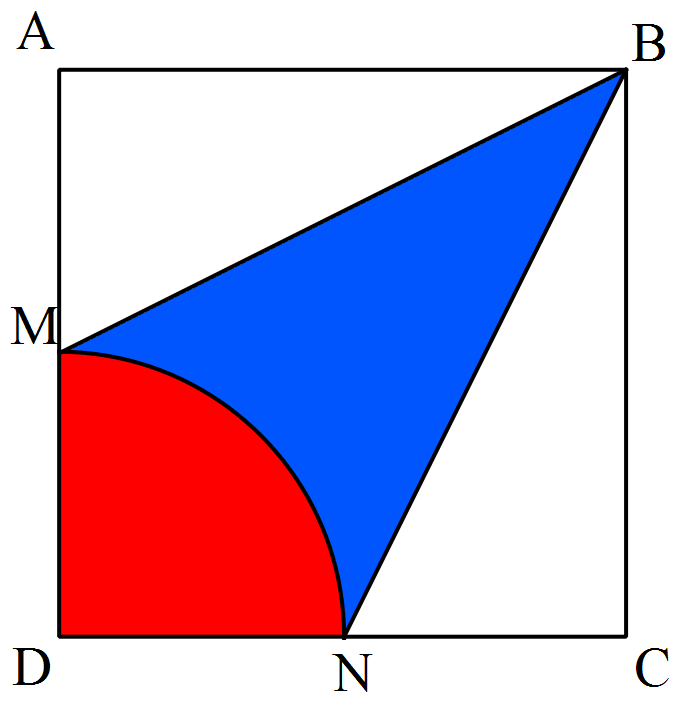
The above shows a square with side length 16.
M and N are midpoints of the sides AD and DC, respectively.
Find the area of the blue region.
The answer is 77.73.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
i'm not a member of brilliant staff ..is this the reason that i am not permitted to post a solution to any problem ??
how can i add a solution to this problem????
Log in to reply
You can only add solutions to problems that you answered correctly. Did you submit the answer of 77.73? I don't see your name in the list of 10 most recent solvers.
Log in to reply
what if i have one now .. best so far ?
Log in to reply
@Ajay Sambhriya – You can post it as a comment or a report, and ask the staff to convert it into a solution.
Log in to reply
@Chung Kevin – but it's a picture ..so how can i post it in comment ?
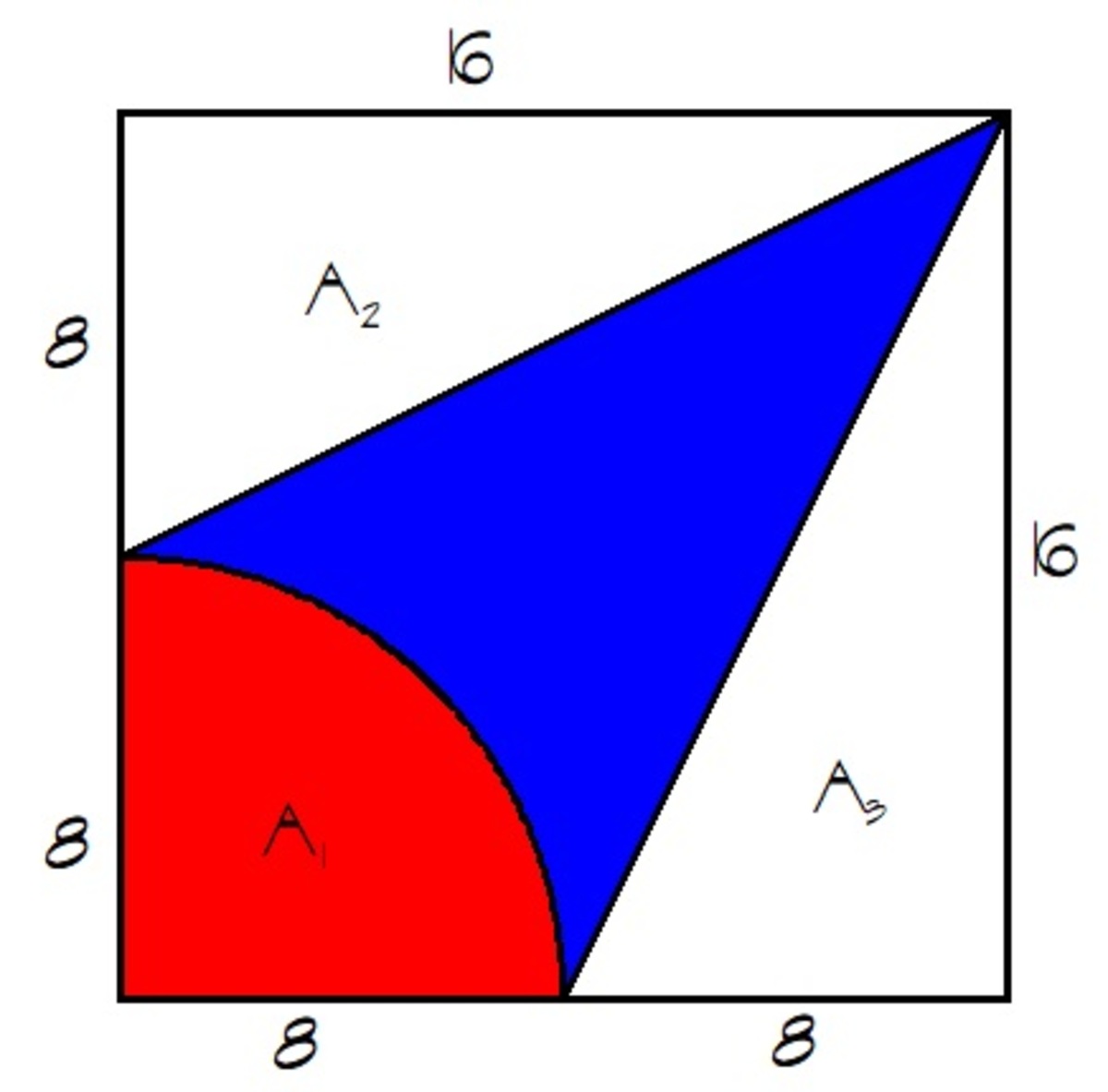 The area of the blue region is equal to the area of the square minus the area of the quarter circle and the two triangles. Considering my diagram, we have
The area of the blue region is equal to the area of the square minus the area of the quarter circle and the two triangles. Considering my diagram, we have
A B L U E = 1 6 2 − A 1 − A 2 − A 3 = 2 5 6 − 4 1 ( π ) ( 8 2 ) − 2 1 ( 8 ) ( 1 6 ) − 2 1 ( 8 ) ( 1 6 ) ≈ 7 7 . 7 3 4 5
Relevant wiki: Length and Area - Composite Figures
Area of triangle A B M + Area of triangle B N C + Area of quarter circle D M N + Area of blue region = Area of square A B C D
Area of triangle A B M = 2 1 × A M × A B = 2 1 × 2 A D × 1 6 = 2 1 × 8 × 1 6 = 6 4 ( 1 ) .
Similarly, Area of triangle B N C = 2 1 × N C × B C = 2 1 × 2 D C × 1 6 = 2 1 × 8 × 1 6 = 6 4 ( 2 ) .
Area of quarter circle D M N = 4 1 π r 2 = 4 1 π ⋅ 8 2 = 1 6 π ( 3 ) .
Area of the square A B C D = 1 6 × 1 6 = 2 5 6 ( 4 ) .
Substitute ( 1 ) , ( 2 ) , ( 3 ) , ( 4 ) into the very first equation gives:
6 4 + 6 4 + 1 6 π + Area of blue region = 2 5 6 ⇒ Area of blue region = 2 5 6 − 6 4 − 6 4 − 1 6 π = 1 2 8 − 1 6 π ≈ 7 7 . 7 3 .