A geometry problem by Andreas Wendler
Two mathematicians are going to shower. Suddenly one says to the other that he had his underpants wrong on. What other possibility is there if he doesn't mean a rotation around z -axis by 1 8 0 ∘ ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Yes, all right (+1). Consider that after reflection outside and inside switch roles => oh!
Log in to reply
How does "mirroring at symmetric plane" work?
Note that "inverting the pants inside out" isn't a "mirror in symmetric plane". In fact, you can't "mirror in symmetric plane" a 3D physical object.
Log in to reply
Sir, I don't know what he though but mirroring at symmetry plane means that mirroring between the two arms of the pair of trousers or whatever we are talking about. Which makes it rotate 180° with z as the axis.
Log in to reply
@Abhay Tiwari – That's a rotation of the pants, instead of a mirroring of the pants.
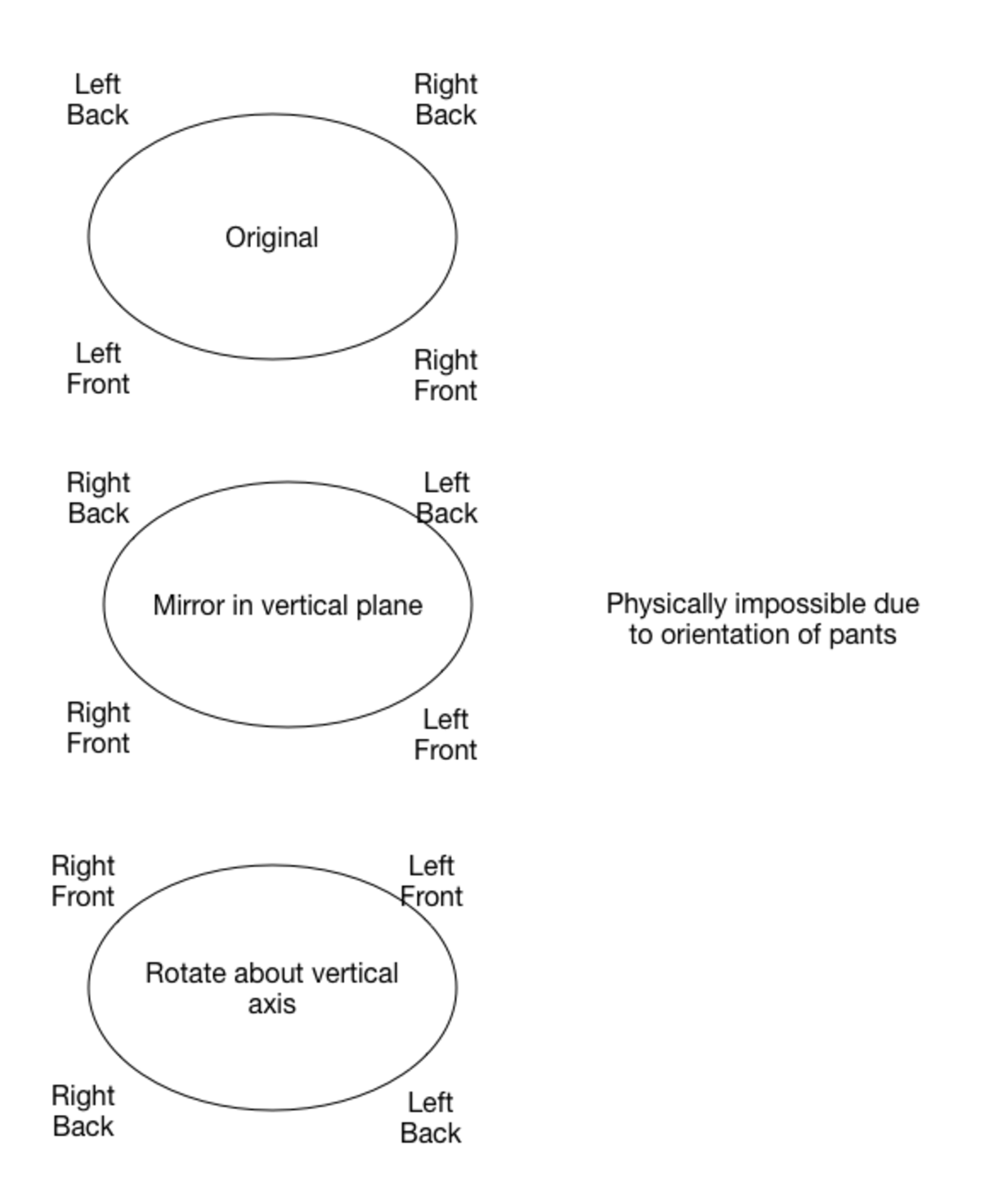
Mirroring at symmetry plane of the underware delivers a self potrait of the pants whereat inside and outside switch. The generatrix of the symmetric plane is the neutral fiber of such rotation-symmetric object like in our case.
Log in to reply
@Andreas Wendler – But sir, I thought that we are mirroring first at the plane of symmetry(I.e. in between the pants), due to which the left becomes right, which is possible only when we rotate it about the z-axiz, please clear my doubt. How are they switching inside out?
Log in to reply
@Abhay Tiwari – Imagine the pants - approximated - as 2 hollow cylinders connected at the upper ends. If one of them is { ( x , y , z ) : r 2 < = x 2 + y 2 < = ( r + d ) 2 , 0 < = z < = h } where d is thickness and h length of the material we have 2 symmetrical surfaces (regarding the left and right part) located exactly in the middle:
{ ( x , y , z ) : [ − ( r + 2 d ) < = x < = 0 ] ∣ [ 0 < x < = ( r + 2 d ) ] , x 2 + y 2 = ( r + 2 d ) 2 , 0 < = z < = h }
These are 2 skin surfaces belonging to one cylinder (=pants' leg) whereat mirroring at them delivers an image with inverted sides of the pants.
The options order shuffle for all people. Please edit your solution.
A)--Displacement by z = + 1 m --no, that means his both legs are in one arms of the underwear.
B)--Rotating around x -axis by 90° ---no again, this means that his underwear has a hole.
C)--Rotating around y -axis by 360°----no, again, this means he is wearing it in a right way.
D)---Mirroring at symmetry plane---yes, he is actually wearing it wrong now.
Ha ha ha, nice question.