A Rose For My Mother

Area of the larger circle= $\frac{22}{7}$ x7x7=154sq.cm (B)

Area of each of the smaller circles= $\frac{22}{7}$ x $\frac{7}{2}$ x $\frac{7}{2}$ = $\frac{77}{2}$ (S)

Area of the overlapping region=A(say)

Area of the shaded region=B-(4S-4A)+4A=B-4S+8A

Area of part A= $\frac{S}{2}$ - $\frac{7}{2}$ x $\frac{7}{2}$

= $\frac{77}{4}$ - $\frac{49}{4}$

= $\frac{28}{4}$

Area of the shaded region=B-4S+8A

=154-4x $\frac{77}{2}$ +8x $\frac{28}{4}$

=56sq.cm

The solution could be better understood by a pic but I don't know how to upload it.

The area of the larger circle are $\frac{22}{7}$ x7x7=154 sq.cm
The area of the smaller circle are $\frac{22}{7}$ x $\frac{7}{2}$ x $\frac{7}{2}=\frac{77}{2}$ sq.cm
Find the area of each yellow shaded part in smaller circle by calculating :
$(\frac{7}{2}$ x $\frac{7}{2}) -$ 2x $(\frac{7}{2}$ x $\frac{7}{2} - \frac{1}{4}$ x $\frac{77}{2})$ = 7 sq.cm (I don't know how to explain this without picture)
$\frac{7}{2}$ is radius for smaller circle.
So, the area of not yellow shaded in each smaller ciclre are $\frac{77}{2}$ - (2x7) = $\frac{49}{2}$
Thus, the area of the part shaded in yellow are 154 - 4x $\frac{49}{2}$ =56 sq.cm

The area of the bigger circle is: $\dfrac{22}{7}\times49=154$

The area of one of the smaller circles: $\dfrac{22}{7}\times\dfrac{7}{2}\times\dfrac{7}{2}=38.5$

Then we need to calculate the area of the intersections of the smaller circles:

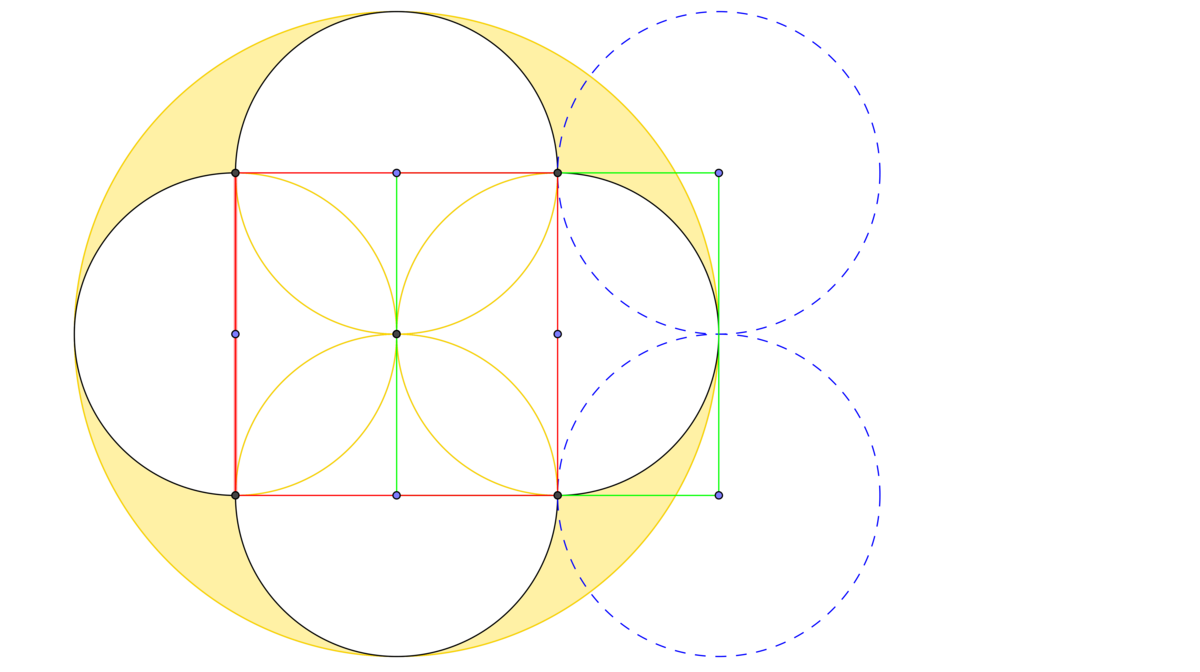
As the image above we can imagine two circles tangent to two of the small circles. We connect the centers of the four circles forming a square (In green), clearly the area of the star of four spikes formed inside the circle equals to: Area of the green square minus Area of a small circle. Then its area is:

$49-38.5=10.5$

We can observe in the image that four of the intersections are formed inside the circle, so the area of the four intersections is:

$49-2(10.5)=49-21=28$

Now, the area of the four circles without it's intersections is:

$4(38.5)-28=154-28=126$

Finally, the area in yellow it's:

$(154-126)+28=\boxed{56}$

you can draw a square in the center by the joining the diameters of the small squares. From this subtract the area of 1 small circle and multiply the answer by 2. You now have the area of the 4 leaf shaped objects. Since the shaded portions all have a ratio of 1:1 multiply the area of one leaf shaped object by 8 and you get 56.

From solving you can subtract the are of 2 leaf shapes from a circle and multiply by 4. this gives you the total unshaded area. Subtracting the 4 leaf shapes from the remainder 56, you can note that each portion has a 1:1 area ratio.

For the area of the inner yellow bits (A): Area of a segment = area of sector - area of isoscoles triangle = (πr^2)*(θ/2π) - 1/2 r^2 sinθ=1/2 r^2(θ-sinθ) θ=π/2 and there are 8 segments, so A=4r^2(π/2-1)

For the area of the outer yellow bits (B): We find the area of the big circle, subtract the area of the 4 smaller circles, then add on the area of the inner bits because they were counted twice when subtracting the smaller circles. So B=πR^2-4πr^2+A But R=2r, so B=4πr^2-4πr^2+A=A

So the total area = A+B=2A=8r^2(π/2-1) Now sub in r=3.5cm and get a final answer of 98(π/2-1)=55.9380400...=55.9cm^2

OR

YOU CAN USE INTEGRATION ALSO AND THE OUTER PART AREA IS EQUAL TO INNER PART

22 7/16 - 49/8 = 3,5 3,5 2= 7 cm² (Área da intersecção entre dois círculos no primeiro quadrante) 22/7 * (7²/2³) - 7 = 12,25 => 2 (12,5) = 24,5 => 24,5 + 7 = 31,5 [22/7 * (7²)]/4 (área do 1º Quadrante) - 31,5 = 7cm² 7 4 + 7*4 = 56

You can replace the yellow areas, so you will have a white square inscribed in the big circle. Then the yellow area is equal to the diference between the circle's area and the square's area, this is 154-98= 56.

Consider smaller circle first and find the area of quarter circle (9.625 sq cm). Find the area of the triangle that forms part of this quarter of the circle (6.125 sq cm). Now subtract the area of the triangle from that of the sector, you get the area under the chord (3.5 sq cm). Double this last are and you get the inner leaf shaped shaded area (7 sq cm). Find the unshaded area of smaller circle subtracting the 2 leaf shaped shaded areas (24.5 sq cm). 4 times of 24.5 (98 sq cm) gives total inner unshaded area. Find the area of the larger circle (154 sq cm). Subtract 98 from 154, we get total shaded area (56 sq cm).

I find a shaded area of quarter of the rose. Then multiply by 4 I find an answer 56. How I make this: First I find the area where two small circles with radii $\frac 72$ are overlapped . I named it C. I find that an area of C is equal to $S_C=2(\frac{\pi(\frac{7}{2})^2}{4} - \frac{(\frac{7}{2})^2}{2} )= 2\frac{7}{2}=7$ . The area outside shaded area ( named it D) is the area of the quarter larger circle minus the area of one smaller circle plus the shaded area C: It all equal to 7, because $S_D=\frac{7^2\pi}{4}-(2.\frac{7^2\pi}{2}-7)=7$ . That is mean $S_c+S_d$ = 14. Then from symmetry I find that 4. 14 = 56 is all shaded area.