Combining 5 Rectangles
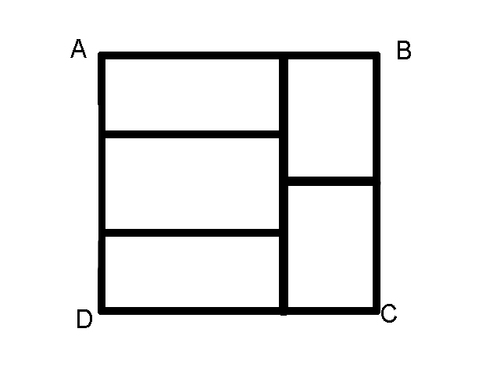Rectangle ABCD (above) is made out of 5 rectangles of equal length and breadth. If the perimeter of ABCD is 44, what is the perimeter of one of these smaller rectangles?
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
from where did u get the specific unit(cm
Log in to reply
He's assuming units. The rest of what he says is correct, albeit confusing.
While I follow what you did, you didn't actually solve for b in the second part and skipped steps that lead your solution to being confusing. the second equation becomes (2a)/3 = b. substituting that in for b in equation 1 results in 4a + (10a)/3 = 44.
multiply everything by 3 get 12a + 10a = 132
combine like terms gets 22a=132
divide by 22 get a=6
plug that into 2a=3b and solve for b you get 2(6)=3b; 12=3b; 4=b.
then 2(6+4) = 20
Log in to reply
Note that 4 a = 2 ( 2 a ) so that what he says is exactly correct.
at first you tell that all 5 rectangles are equal but at last you asked the smallest rectangle? this is confusing
not good BC is 11 and half i s 5.5; which should be longer side of rectangle. If you say that smaller is 6 and 4 than 5 * 24 = 120 and whole area is 11 * 11 = 121. Largest rec 1 cm^2?
Log in to reply
How did you determine BC as 11, it would be 12 BC is 2 times the length of the smaller rectangle. Which is 2(6). Gives you BC as 12 and AB would be 6+4 = 10.
Area of ABCD = 12(10) = 120
Area of 5 smaller rectangles = 5(lb) = 5(6*4) = 120
It has to be quad. 11 * 11 otherwise there is no area differential left for larger rectangle.
Log in to reply
It cannot be a square. If it was a square, the smaller rectangles would not all be the same size. Just because it was drawn inaccurately (or so it appears) doesn't mean that the drawing dictates the size.
You are right.. But it has a single problem in your answer.. You write answer in 20 cm, But the answer should be unit less as we don't know the unit of parameter of rectangle ABCD.. So, the unit of our answer will be same as unit of that parameter.. So the answer is 20 not 20cm..
simple and intelligent. good approach keep it up
I'm not convinced. by the logic. If the perimeter is 44, A to B is 11. Therefore... the side of a rectangle plus its end is also 11. That happens twice so the answer should be 22. Where am I wrong?
Log in to reply
OK. I thought it was creating a square but, of course, it isn't. A to B can not be the same as B to C.... it just looks as if it is.
kumar's solution is best!
Applicative solution
that would only give an original perimeter of 40
Log in to reply
No, it would not. The right side is 6+6, or 12, and the bottom side is 6+4, or 10. 12+10 = 22. 22+22 = 44.
I do not think this can be a possible solution. If it works it should work for any/all possible rectangles with perimeter equaling 44. Continue assuming ABCD is a rectangle. AB=CD and BC = AD. Let us assume AB = 20 then AD must equal 2 to give us a perimeter of 44. Also this gives an area of 40. Using the solution above the area of each smaller rectangle is 6x4 = 24. 5x24 = 120. 120!=40. We know the 5 smaller rectangles are contained in the larger rectangle, therefore this solution can not be correct. I do not think we have enough information to properly solve this problem.
Define short side unit as a. Long side unit is b.
2(l+w) = 44 Perimeter
3a= 2b sides of rectangle are equal
3/2a= b multiplied both by 1/2
2(3a + 3/2a) = 44
6a + 18a/2 = 44
6a + 9a = 44
a= 44/15 =2.9333 =a
3x 2.9333 = 8.79 x 2= 17.58
44 - 17.58 = 26.42 /2 =13.21
13.21- 2.93 = 10.28
Perimeter of smaller rectangle is
2(2.93+ 10.28) = 26.42
I think that this answer is incorrect. The image given with the problem does not lend itself to the assumptions he makes. (ie. "AD=BC or a+a=b+b+b") Is he drawing lines on the figure to see if b+b+b is equal to AB? There is no mathematical answer to this problem, purely a guessing and estimating answer. Please remove this problem for being incomplete and childish. If I wanted to return to freshman year geometry I would.
Log in to reply
The picture is wrongly given in the form of a square, though they have already mentioned it to be a rectangle.
The opposite sides of a rectangle are of equal length. AD and BC are opposite sides of the given rectangle.
If ABCD is a rectangle, then AD=BC by definition. Given in the problem, the 5 rectangles that are drawn inside ABCD are congruent. Therefore, if AD = b+b+b and BC = a + a, then b+b+b = a+a.
AD must = BC to satisfy the statement ADCD is a rectangle. So AB =10 and BC =12 thus giving 44 perimeter of ABCD Aniket Kumar is correct!
Log in to reply
It can not be rectangle because 5 * 24 is 120. There is no extra area for larger rectangle.
Log in to reply
@Dervis Mahmutcehajic – AB =10, BC=12 so area =120 as is the sum of the areas of the 5 off 6 * 4 rectangles.
Log in to reply
@Alan Light – I am stupid. For some reason I thought that one rectangle is larger. Thanks.
dude go solve it first think a bit go to school and learn some math its perfect question and a tricky too
AD does equal BC because opposite sides of a rectangle are equal length.
David, The problem clearly states that ABCD is a rectangle. So it is fair to assume AB = DC and AD = BC
not satisfied
so first we can tell that the length of segment BC and AD will be a multiple of both 3 and 2, because assuming the dimensions of the small rectangles to be integral, the length of BC and AD can both accommodate 3 widths of the smaller rectangle or 2 lengths. So, we find the most basic possible length of BC or AD. This would be 6 because it is the LCM of 3 and 2.
Then, we know that the length of AB and DC is the sum of the length and width or one small rectangle. Since the length of BC and AD are 6, the two dimensions of the smaller rectangle would be 3 x 2. Therefore, AB and DC would both be a length of 5.
Therefore, we now know that the dimensions of the large rectangle are at a 5:6 ratio. By assuming 5 and 6 are the dimensions of the rectangle, we find the perimeter of the large rectangle to get 22. This means that by doubling it, we can achieve 44.
Therefore, we double each dimension of the larger rectangle to get a perimeter of 44. The new dimensions would be 10 x 12. This means that the dimensions of the smaller rectangles would be 4 x 6, because three 4's go into 12 and 2 6's go into 12. The perimeter of the smaller rectangle is therefore 2(6) + 2(4) = 20
From the diagram BC = AD. BC is made of 2 long(L), AD is made of 3 short(S), therefore 2 L equal 3 S. 2L = 3S or L = 1.5S given 44 = 2L + 2S substituting in the above, 44 = 3S + 2S, = 5S S = 44/5 = 8.8 L = 1.5S =13.2 This works with the larger perimeter L+L+S+S or 8.8+8.8+13.2+13.2 = 44 For the smaller rect we know 2L=13.2, L = 6.6 2L = 3S so S = 2.2 smaller perim of S+S+L+L or 2.2+2.2+6.6+6.6= 17.6
Ryan you are correct. 20 is the correct answer
To start off, I put the side lengths of the smaller rectangles in terms of x. The shorter side was 1x and I found the longer side would be 1.5x because 3 shorter sides are the same length as 2 long sides (3x=2x -> 1.5x=1x). This would make AB=2.5x and BC=3x. The total perimeter would be 11x since AB=DC and BC=AD. Solving for x, I got x=4 (44=11x -> 4=x). To finish up the problem, I found the perimeter in terms of x for the smaller rectangles (1.5x+1.5x+1x+1x=5x) and I plugged in 4 for x.
I HAVE ANOTHER IDEA... y=length and x=breadth we know this fact 5x+4y=44 and 3x=2y because the breadths of our main rectangle are same then this equation is right (3x=2y) well.....we have two equation and two variable and we can solve our problem.
Let L and B be the length and breadth of rect ABCD . 2(L+B)=44.........given.
L+B=22.....................(1). Let l and b be the length and breadth of small rectangle.
Now take sides AB and BC, we get the equation. (l+b)+(l+l)=22 3l+b=22.......................(2)
Similarly take sides AB and AD, we get (l+b)+(3b)=22 l+4b=22..............(3)
Now multipy equation 3 by 3...and solve them simultaneosly
b=4 solving we get l=6
hence perimeter of small rectangle is
2(l+b)=2(6+4)=20.............ans
Let's call the upper right corner of the middle rectangle point E, the unlabeled corner on the top side of the large rectangle point F, the unlabeled corner on the right side of the large rectangle point G, and the corner just to the left of point G point H.
Furthermore, let's say that the length of line segment EH is equal to x. Since we know that all five smaller rectangles have equal dimensions, we can quickly deduce that the length of line segment EF is 2x, and that the length of line segment FH is 3x, as x + 2x = 3x. Now we know that the dimension of each smaller rectangle is 6x (3x+3x) by 5x (3x+2x).
Using this logic, we can see that the perimeter of the large rectangle is equal to 22x (6x+6x+5x+5x = 12x+10x = 22x). Since we also know that the perimeter of the large rectangle is 44, we can confidently say that 22x = 44. Divide both sides by 22, and you can see that x = 2.
The dimensions of each of the smaller rectangles are 2x by 3x, or 4 (2 times 2) by 6 (2 times 3). To obtain perimeter of a rectangle, add two adjacent sides and multiply by two. 2*(4+6) = 2 times 10 = 20.
4L + 4W = 44, hence L+ W =11
Area of ABCD = AB x BC = (W+ L) x2L= 22L
Similarly;
Area of ABCD = AB x AD= (W+ L) x3W =33W
Also;
Area of ABCD = sum of 5 smaller rectangles = 5LW
Hence; L=33/5 and W= 22/5
Therefore, perimeter of 1 rectangle = (22+22+33+33)/5 = 100/5 = 20
Let l =A
b =B
P= 44
44/2= 22
AB +BC =22
A+B+A+A= 22 (1)
AD+DC = 22 B+B+B+A+B= 22 (2) ADDING (1) & (2) A+B+A+A = B+B+B+A+B A+A = B+B+B 2A=3B A= 2B/3 B= 2A/3
FROM (1) A+B+A+A =22 A+2A/3 +A+A =22 11A/3 = 22 11A = 66 A= 6 B=2A/3 =12/3 =4
P= 2(l+b) P= 2(A+B) =2(6+4) =2*10 = 20 units
I took a very different approach take the right side and the bottom side of the rectangle ABCD it is formed by 3 rectangles and it can be written as h +3w =22 --- ( i )
the left side can be written as 4h + w = 22 --- ( ii ) simple simultaneous equation solving gives you w = 6 and height = 4 add them up and multiply by 2 = 20
Perimeter of ABCD = 44 let length of smaller rectangles = a & breadth of smaller rectangles = b
Now, Perimeter of ABCD = a+b+a+a+a+b+b+b+b = 44 or, 4a+5b=44.......................................(1)
Also, AD=BC or, a+a = b+b+b or, 2a=3b ...............................................(2)
putting value of '2a' in (1), we get b=4 ...................................(3)
putting value of 'b' in (1) or (2), we get a=6 .......................................(4)
So, perimeter of the smaller rectangle is, preimeter = 2(a+b) = 2(6+4) = 2(10) = 20 cm (Ans)