Checkerboard Triangle Again

@Michael Mendrin Yea, the calculations are a ton worse than I expected.

I've been trying to do a continuity argument from the even-even to the even-odd to the odd-odd case, but that doesn't seem to lead me anywhere.

IE In the 4 by 6, the yellow and pink areas are the same. So let's consider the additional triangle with vertices $(0,4), (6,0), (7,0)$ . But, that would cause me to think that the pink area is larger, mainly because of the bottom right triangle.

I suspect it has some number-theoretic relevance / consequence, and might try phrasing it that way.

Given the integer sides of the triangle $a,b$ of opposite parity, the following generates the fraction $F(a,b)$ that is the absolute difference between the total area of either color with half of the area of the triangle

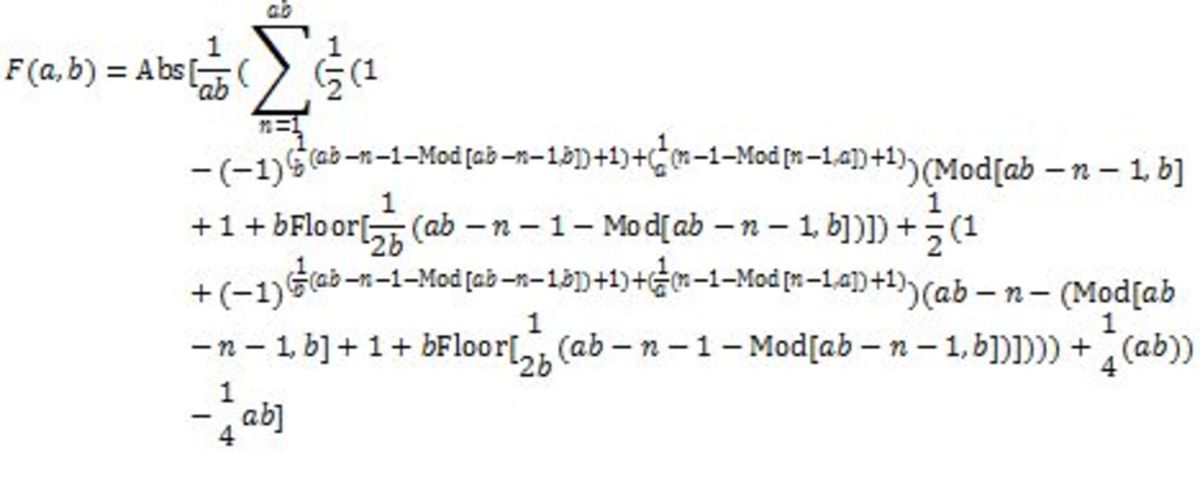
So, for example, for $a=4$ , and $b=7$ , the absolute difference is $\dfrac{1}{28}$

Results in form of $a$ , $b$ , and $F(a,b)$

$\begin{array}{ccc|} a & b & F(a,b) \\ \hline 2 & 3 & \frac{1}{12} \\ 2 & 5 & \frac{1}{20} \\ 2 & 7 & \frac{1}{28} \\ 2 & 9 & \frac{1}{36} \\ 2 & 11 & \frac{1}{44} \\ 2 & 13 & \frac{1}{52} \\ 2 & 15 & \frac{1}{60} \\ 2 & 17 & \frac{1}{68} \\ 2 & 19 & \frac{1}{76} \\ 2 & 21 & \frac{1}{84} \\ 2 & 23 & \frac{1}{92} \\ 2 & 25 & \frac{1}{100} \\ 2 & 27 & \frac{1}{108} \\ 2 & 29 & \frac{1}{116} \\ 2 & 31 & \frac{1}{124} \\ 2 & 33 & \frac{1}{132} \\ 2 & 35 & \frac{1}{140} \\ 2 & 37 & \frac{1}{148} \\ 2 & 39 & \frac{1}{156} \\ 2 & 41 & \frac{1}{164} \\ 2 & 43 & \frac{1}{172} \\ 2 & 45 & \frac{1}{180} \\ 2 & 47 & \frac{1}{188} \\ 2 & 49 & \frac{1}{196} \\ 2 & 51 & \frac{1}{204} \\ 2 & 53 & \frac{1}{212} \\ 2 & 55 & \frac{1}{220} \\ 2 & 57 & \frac{1}{228} \\ 2 & 59 & \frac{1}{236} \\ 2 & 61 & \frac{1}{244} \\ \end{array}$ $\begin{array}{ccc|} a & b & F(a,b) \\ \hline 4 & 3 & \frac{5}{12} \\ 4 & 5 & \frac{1}{4} \\ 4 & 7 & \frac{1}{28} \\ 4 & 9 & \frac{1}{36} \\ 4 & 11 & \frac{5}{44} \\ 4 & 13 & \frac{5}{52} \\ 4 & 15 & \frac{1}{60} \\ 4 & 17 & \frac{1}{68} \\ 4 & 19 & \frac{5}{76} \\ 4 & 21 & \frac{5}{84} \\ 4 & 23 & \frac{1}{92} \\ 4 & 25 & \frac{1}{100} \\ 4 & 27 & \frac{5}{108} \\ 4 & 29 & \frac{5}{116} \\ 4 & 31 & \frac{1}{124} \\ 4 & 33 & \frac{1}{132} \\ 4 & 35 & \frac{1}{28} \\ 4 & 37 & \frac{5}{148} \\ 4 & 39 & \frac{1}{156} \\ 4 & 41 & \frac{1}{164} \\ 4 & 43 & \frac{5}{172} \\ 4 & 45 & \frac{1}{36} \\ 4 & 47 & \frac{1}{188} \\ 4 & 49 & \frac{1}{196} \\ 4 & 51 & \frac{5}{204} \\ 4 & 53 & \frac{5}{212} \\ 4 & 55 & \frac{1}{220} \\ 4 & 57 & \frac{1}{228} \\ 4 & 59 & \frac{5}{236} \\ 4 & 61 & \frac{5}{244} \\ \end{array}$ $\begin{array}{ccc|} a & b & F(a,b)| \\ \hline 6 & 3 & \frac{1}{4} \\ 6 & 5 & \frac{7}{12} \\ 6 & 7 & \frac{5}{12} \\ 6 & 9 & \frac{1}{12} \\ 6 & 11 & \frac{1}{44} \\ 6 & 13 & \frac{1}{52} \\ 6 & 15 & \frac{1}{20} \\ 6 & 17 & \frac{35}{204} \\ 6 & 19 & \frac{35}{228} \\ 6 & 21 & \frac{1}{28} \\ 6 & 23 & \frac{1}{92} \\ 6 & 25 & \frac{1}{100} \\ 6 & 27 & \frac{1}{36} \\ 6 & 29 & \frac{35}{348} \\ 6 & 31 & \frac{35}{372} \\ 6 & 33 & \frac{1}{44} \\ 6 & 35 & \frac{1}{140} \\ 6 & 37 & \frac{1}{148} \\ 6 & 39 & \frac{1}{52} \\ 6 & 41 & \frac{35}{492} \\ 6 & 43 & \frac{35}{516} \\ 6 & 45 & \frac{1}{60} \\ 6 & 47 & \frac{1}{188} \\ 6 & 49 & \frac{1}{196} \\ 6 & 51 & \frac{1}{68} \\ 6 & 53 & \frac{35}{636} \\ 6 & 55 & \frac{7}{132} \\ 6 & 57 & \frac{1}{76} \\ 6 & 59 & \frac{1}{236} \\ 6 & 61 & \frac{1}{244} \\ \end{array}$ $\begin{array}{ccc|} a & b & F(a,b) \\ \hline 8 & 3 & \frac{1}{6} \\ 8 & 5 & \frac{3}{10} \\ 8 & 7 & \frac{3}{4} \\ 8 & 9 & \frac{7}{12} \\ 8 & 11 & \frac{3}{22} \\ 8 & 13 & \frac{1}{26} \\ 8 & 15 & \frac{1}{60} \\ 8 & 17 & \frac{1}{68} \\ 8 & 19 & \frac{1}{38} \\ 8 & 21 & \frac{1}{14} \\ 8 & 23 & \frac{21}{92} \\ 8 & 25 & \frac{21}{100} \\ 8 & 27 & \frac{1}{18} \\ 8 & 29 & \frac{1}{58} \\ 8 & 31 & \frac{1}{124} \\ 8 & 33 & \frac{1}{132} \\ 8 & 35 & \frac{1}{70} \\ 8 & 37 & \frac{3}{74} \\ 8 & 39 & \frac{7}{52} \\ 8 & 41 & \frac{21}{164} \\ 8 & 43 & \frac{3}{86} \\ 8 & 45 & \frac{1}{90} \\ 8 & 47 & \frac{1}{188} \\ 8 & 49 & \frac{1}{196} \\ 8 & 51 & \frac{1}{102} \\ 8 & 53 & \frac{3}{106} \\ 8 & 55 & \frac{21}{220} \\ 8 & 57 & \frac{7}{76} \\ 8 & 59 & \frac{3}{118} \\ 8 & 61 & \frac{1}{122} \\ \end{array}$ $\begin{array}{ccc|} a & b & F(a,b) \\ \hline 10 & 3 & \frac{19}{60} \\ 10 & 5 & \frac{1}{4} \\ 10 & 7 & \frac{51}{140} \\ 10 & 9 & \frac{11}{12} \\ 10 & 11 & \frac{3}{4} \\ 10 & 13 & \frac{51}{260} \\ 10 & 15 & \frac{1}{12} \\ 10 & 17 & \frac{19}{340} \\ 10 & 19 & \frac{1}{76} \\ 10 & 21 & \frac{1}{84} \\ 10 & 23 & \frac{19}{460} \\ 10 & 25 & \frac{1}{20} \\ 10 & 27 & \frac{17}{180} \\ 10 & 29 & \frac{33}{116} \\ 10 & 31 & \frac{33}{124} \\ 10 & 33 & \frac{17}{220} \\ 10 & 35 & \frac{1}{28} \\ 10 & 37 & \frac{19}{740} \\ 10 & 39 & \frac{1}{156} \\ 10 & 41 & \frac{1}{164} \\ 10 & 43 & \frac{19}{860} \\ 10 & 45 & \frac{1}{36} \\ 10 & 47 & \frac{51}{940} \\ 10 & 49 & \frac{33}{196} \\ 10 & 51 & \frac{11}{68} \\ 10 & 53 & \frac{51}{1060} \\ 10 & 55 & \frac{1}{44} \\ 10 & 57 & \frac{1}{60} \\ 10 & 59 & \frac{1}{236} \\ 10 & 61 & \frac{1}{244} \\ \end{array}$ $\begin{array}{ccc|} a & b & F(a,b) \\ \hline 12 & 3 & \frac{1}{4} \\ 12 & 5 & \frac{13}{60} \\ 12 & 7 & \frac{25}{84} \\ 12 & 9 & \frac{5}{12} \\ 12 & 11 & \frac{13}{12} \\ 12 & 13 & \frac{11}{12} \\ 12 & 15 & \frac{1}{4} \\ 12 & 17 & \frac{25}{204} \\ 12 & 19 & \frac{13}{228} \\ 12 & 21 & \frac{1}{28} \\ 12 & 23 & \frac{1}{92} \\ 12 & 25 & \frac{1}{100} \\ 12 & 27 & \frac{1}{36} \\ 12 & 29 & \frac{13}{348} \\ 12 & 31 & \frac{25}{372} \\ 12 & 33 & \frac{5}{44} \\ 12 & 35 & \frac{143}{420} \\ 12 & 37 & \frac{143}{444} \\ 12 & 39 & \frac{5}{52} \\ 12 & 41 & \frac{25}{492} \\ 12 & 43 & \frac{13}{516} \\ 12 & 45 & \frac{1}{60} \\ 12 & 47 & \frac{1}{188} \\ 12 & 49 & \frac{1}{196} \\ 12 & 51 & \frac{1}{68} \\ 12 & 53 & \frac{13}{636} \\ 12 & 55 & \frac{5}{132} \\ 12 & 57 & \frac{5}{76} \\ 12 & 59 & \frac{143}{708} \\ 12 & 61 & \frac{143}{732} \\ \end{array}$ $\begin{array}{ccc|} a & b & F(a,b) \\ \hline 14 & 3 & \frac{17}{84} \\ 14 & 5 & \frac{3}{28} \\ 14 & 7 & \frac{1}{4} \\ 14 & 9 & \frac{79}{252} \\ 14 & 11 & \frac{145}{308} \\ 14 & 13 & \frac{5}{4} \\ 14 & 15 & \frac{13}{12} \\ 14 & 17 & \frac{145}{476} \\ 14 & 19 & \frac{79}{532} \\ 14 & 21 & \frac{1}{12} \\ 14 & 23 & \frac{15}{644} \\ 14 & 25 & \frac{17}{700} \\ 14 & 27 & \frac{1}{108} \\ 14 & 29 & \frac{1}{116} \\ 14 & 31 & \frac{17}{868} \\ 14 & 33 & \frac{5}{308} \\ 14 & 35 & \frac{1}{20} \\ 14 & 37 & \frac{79}{1036} \\ 14 & 39 & \frac{145}{1092} \\ 14 & 41 & \frac{65}{164} \\ 14 & 43 & \frac{65}{172} \\ 14 & 45 & \frac{29}{252} \\ 14 & 47 & \frac{79}{1316} \\ 14 & 49 & \frac{1}{28} \\ 14 & 51 & \frac{5}{476} \\ 14 & 53 & \frac{17}{1484} \\ 14 & 55 & \frac{1}{220} \\ 14 & 57 & \frac{1}{228} \\ 14 & 59 & \frac{17}{1652} \\ 14 & 61 & \frac{15}{1708} \\ \end{array}$ $\begin{array}{ccc|} a & b & F(a,b) \\ \hline 16 & 3 & \frac{7}{24} \\ 16 & 5 & \frac{3}{8} \\ 16 & 7 & \frac{3}{14} \\ 16 & 9 & \frac{5}{18} \\ 16 & 11 & \frac{31}{88} \\ 16 & 13 & \frac{55}{104} \\ 16 & 15 & \frac{17}{12} \\ 16 & 17 & \frac{5}{4} \\ 16 & 19 & \frac{55}{152} \\ 16 & 21 & \frac{31}{168} \\ 16 & 23 & \frac{5}{46} \\ 16 & 25 & \frac{3}{50} \\ 16 & 27 & \frac{5}{72} \\ 16 & 29 & \frac{7}{232} \\ 16 & 31 & \frac{1}{124} \\ 16 & 33 & \frac{1}{132} \\ 16 & 35 & \frac{1}{40} \\ 16 & 37 & \frac{15}{296} \\ 16 & 39 & \frac{1}{26} \\ 16 & 41 & \frac{5}{82} \\ 16 & 43 & \frac{31}{344} \\ 16 & 45 & \frac{11}{72} \\ 16 & 47 & \frac{85}{188} \\ 16 & 49 & \frac{85}{196} \\ 16 & 51 & \frac{55}{408} \\ 16 & 53 & \frac{31}{424} \\ 16 & 55 & \frac{1}{22} \\ 16 & 57 & \frac{1}{38} \\ 16 & 59 & \frac{15}{472} \\ 16 & 61 & \frac{7}{488} \\ \end{array}$