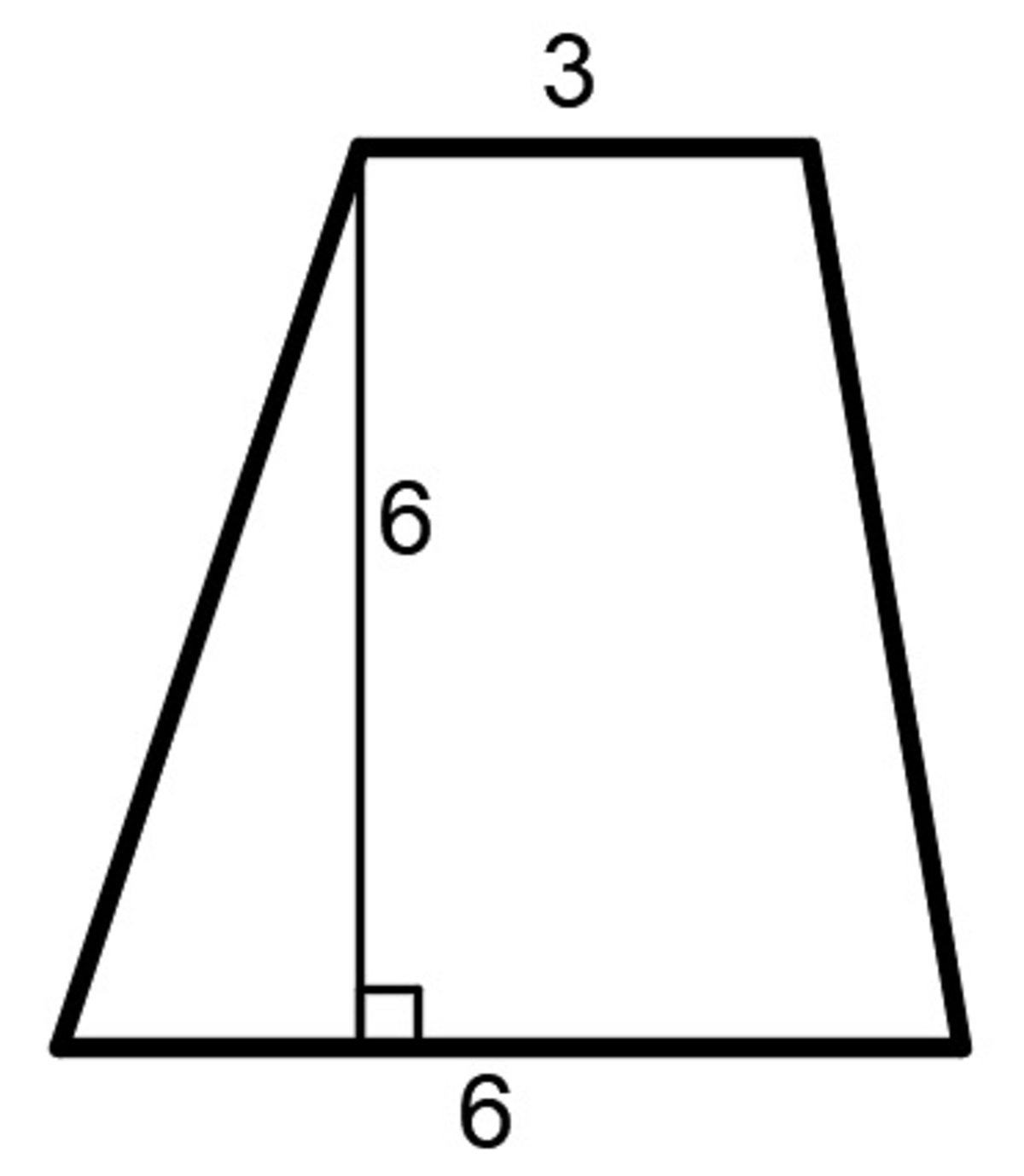
Tall, Tall Trapezium

There is a direct formula for finding the area of a trapezium, i.e. $\dfrac{h×(a+b)}{2}$

Where h = height = 6 units,

a= length of one parallel side = 3,

b = length of the other parallel side = 6 units

Therefore the area of this trapezium, $=\dfrac{6×(3+6)}{2} \\ = 3×9 \\ = \boxed{27}$

This trapezium has three parts (from left to right) - Part 1 - Haf of 12 squares (=6) + Part 2 - 18 full squares + Part3 - Half of 6 squares (3) = 27

As you can tell off the bat the entire square has an area of 36 (6X6) except you are missing parts on the left and right. On the left you are missing half of a 1X6 column = 3, and on the left missing half of a 2X6 column = 6. Subtract to find the total: 36-3-6 =27

What I did - split trapezium into three parts (from left to right):

1. Right angled triangle nr.1 which has a surface: P1=2*6/2 =6
2. The rectangle with surface of: P2=3*6=18
3. Right angled triangle nr.2 and its surface is: P3=1*6/2=3

The end result (surface of the trapezium) is simply all these three surfaces added together:

P=P1+P2+P3=6+18+3=27

The area of the triangles are (2x6)/2+(1x6)/2= 9. The square area is 36. 36-9=27

Bottom base: 6 Top base: 3 Height: 6 Area of a trapezoid formula: height times (top base + bottom base) all divided by 2 Area = 27

One can use Pick's Theorem and count the number of points in the grid that lay on the border of the teapezoid (B), count the number of points that are in the interior of the figure (I) and use the formula:

$\frac{B}{2}+I+1$

Since:

$B=12$

$I=21$

The correct answer is:

$\frac{12}{2}+21+1=27$

The area of the trapezium is $\frac{h(a+b)}{2}$

Where $h$ is height which is 6, $a$ is $parallel_1=3$ & $b$ is $parallel_2=6$

So the area of the given trapezium is:

$\frac{6(3+6)}{2}=3(3+6) = 3 \times 9=27$

The formula for a trapezoid (U.S. English; trapezium in British English) is the easiest way to solve this, as other solvers have done.

But I want to introduce Pick's Theorem, which says that for a polygon whose vertices fall on an integer lattice, the area is equal to $i + \frac{b}{2} - 1$ , where $i$ is the number of lattice points in the interior of the polygon, and $b$ is the number of lattice points on the boundary.

To check, let $i = 22$ and $b = 12$ . Then $i + \frac{b}{2} - 1 = 22 + \frac{12}{2} - 1 = 22 + 6 - 1 = \boxed{27}$ .

$A = \dfrac{1}{2}(a+b)h=\dfrac{1}{2}(3+6)6 = \boxed{27}$

There are 2 ways to do this. Firstly, you can just count up the squares, with the central, rectangular portion being 18 unit squares. The triangular piece on the left is (1/2) of 12, or 6. And the other triangular piece is (1/2) of 6, or 3. That's 18 + 6 + 3 = 27

The other method is the trapezium formula. There are many equivalent ways to write down this formula, but the one that I found most useful for this problem is: (a + b) x $\frac{h}{2}$

With a and b being the parallel sides of the trapezium; and h being the height.

So, that's (3 + 6) x $\frac{6}{2}$ or 9 x 3 = 27

Just to say, it's called a trapezium in the UK too.

I counted solid blue squares. Looked at remaining squares and determined which squares would complete one solid square. These combined squares counted as a single additional square to the solid ones. So, I visualized the answer and got 27. No, I didn't print and cut anything out. Just looked at it a couple minutes.

I will give a straightforward approach; By Pick's Theorem AREA of a non-intersecting planar graph =(No. of internal vertices)-(half of the no. of external vertices)-1

🔴Tips to solve this problem⤵️:

🔵What is the area of the big square: c✖️c=6️⃣✖️6️⃣= 3️⃣6️⃣

🔵What is the area of both white triangles:

🔘Area of the big one: Base✖️Height➗2= 2️⃣✖️6️⃣➗2️⃣= 6️⃣

🔘Area of the small one: B✖️H➗2=1️⃣✖️6️⃣➗2️⃣= 3️⃣

🔘Area of both white triangles: 6️⃣➕3️⃣= 9️⃣

🔵Required Area( blue trapezium )= Area of the square ➖Area of both

triangles=3️⃣6️⃣➖9️⃣= 2️⃣7️⃣

Break it into 3 regions: the left triangle (half of 6x2), the middle rectangle (6x3), and the right triangle (half of 6x1), the area is the sum of three: 0.5 6 2+6 3+0.5 6*1=6+18+3=27

It's not trapezium, it's trapezoid.

A quadrilateral who has two parallel and two non parallel sides is known as trapezoid.

A non standard quadrilateral is called a trapezium.

Area of trapezoid = (Sum of parallel sides)*(distance of parallel sides)/2

Area = (3+6)(6)/2 =27

Area of Trapezium = 1/2xh(a+b) = 1/2 x 6x(6 + 3) =3 x (9) = 27

6^2-1/2x2x6-1/2x1x6=27

0.5x(sum of parallel arms)x parallel distance

so, 0.5x(6+3)x6=27

Just divided it into 3parts*: rectangle and two triangles.. And adding the areas obtained by their respective formulas..