Angle ratios
Triangle A B C has side lengths A B = 4 , B C = 5 , and C A = 6 .
How many times larger is the largest angle of the triangle than the smallest angle?
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
This is the easiest way I found (without a calculator of course).
Log in to reply
We needed to know that the answer was 2, in order to (reasonably) proceed with this solution. So, how could we have known that the answer is 2?
Log in to reply
You can't really - there is a way to solve the problem without making a postulation, but it's nowhere near as neat. You have to use the cosine rule and some angle addition identities. There are also some holes that need to be patched when you use this method if the solution is to be foolproof. You really do need to just examine the triangle, and then attempt to prove that it is 2. Anyone have any other solutions that don't require this guess at the start?
Log in to reply
@Miles Koumouris – Not really. The generalized solutions that I have all compare cosine / sine of the angles, and hope they cancel out nicely, which isn't guaranteed.
It's worthwhile to be explicit about what we're doing at the start of the solution, so that others are prepared when they are reading through the solution.
Log in to reply
@Calvin Lin – I've added a sentence near the start to clarify the direction of the proof.
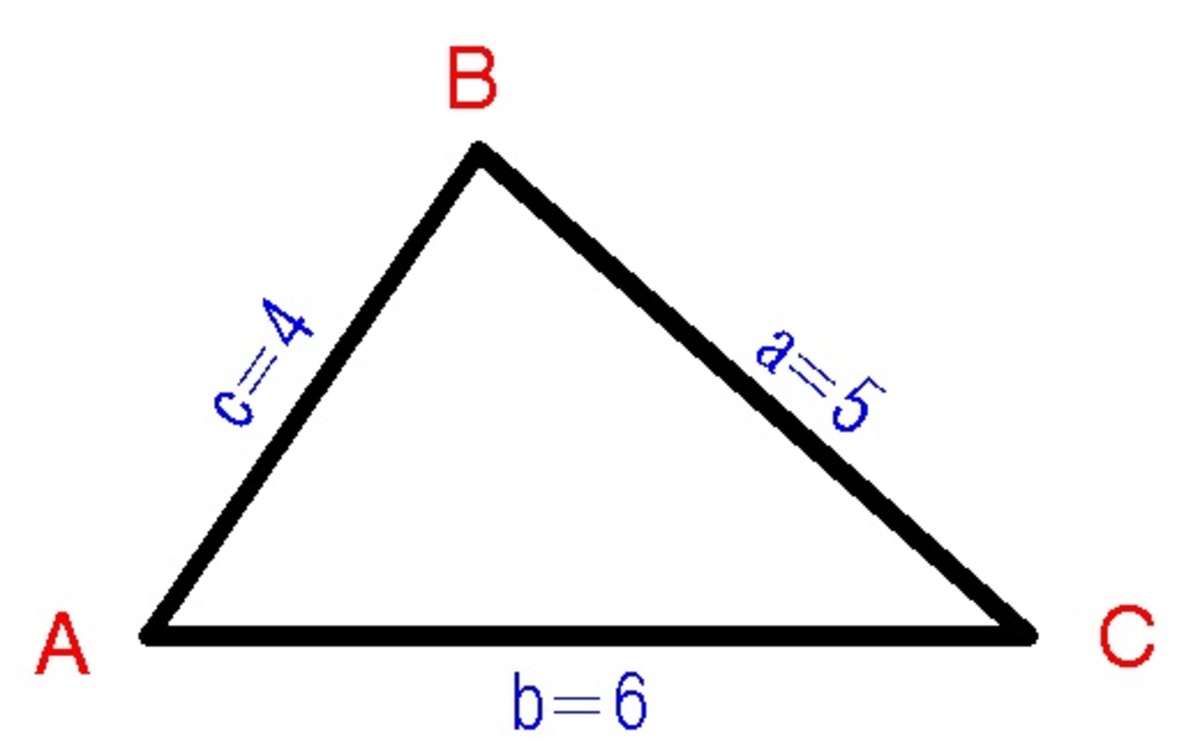 The largest angle in a triangle is always opposite the longest side while the smallest angle is always opposite the shortest side. From the figure,
∠
B
is the largest while
∠
C
is the smallest.
The largest angle in a triangle is always opposite the longest side while the smallest angle is always opposite the shortest side. From the figure,
∠
B
is the largest while
∠
C
is the smallest.
By Cosine Law, we have
6 2 = 4 2 + 5 2 − 2 ( 4 ) ( 5 ) c o s B ⟹ ∠ B = 8 2 . 8 1 9 2 4 4 2 2 ∘
4 2 = 5 2 + 6 2 − 2 ( 5 ) ( 6 ) c o s C ⟹ ∠ C = 4 1 . 4 0 9 6 2 2 1 1 ∘
It follows that,
∠ C ∠ B = 2
∴ ∠ B is two times larger than ∠ C
Since the largest angle subtends the largest side, we have ∠ A B C > ∠ B A C > ∠ B C A , so we are trying to find the value of a , where ∣ ∠ A B C ∣ = a ∣ ∠ B C A ∣ .
This is because the largest angle of a triangle is always opposite the longest side, and the smallest angle is always opposite the smallest side.
We conjecture a = 2 , and so must prove ∣ ∠ A B C ∣ = 2 ∣ ∠ B C A ∣ .
Let the angle bisector of ∠ A B C meet A C at D . Then by the Angle bisector theorem
D C A D = B C A B = 5 4 .
We also know that A D + D C = 6 , so
5 4 D C + D C = 6 ⟹ D C = 9 3 0 and A D = 9 2 4 .
Now A B A D = 9 × 4 2 4 = 3 2 = A C A B , and since ∠ B A D = ∠ B A C , we know that
△ B A D ∼ △ C A B ⟹ ∠ A B D = ∠ B C A .
Finally, since ∠ A B D = 2 1 ∠ A B C , we know that ∠ A B C = 2 ∠ B C A .
Hence, a = 2 .