Which center are we referring to again?

Geometry Level 5

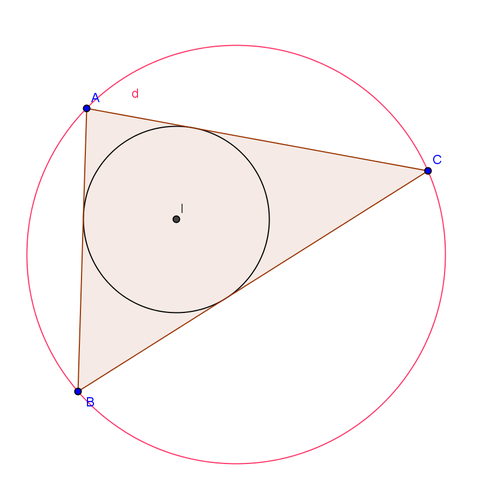Given the triangle A B C ABC with vertices on a circle such that A B ‾ = 11 , B C ‾ = 13 , C A ‾ = 16 \overline { AB } =11,\quad \overline { BC } =13,\quad \overline { CA } =16

Let I I be the incenter and O O the circumcenter.

If the value of I O ‾ 2 \overline { IO }^2 is of the form x y \frac { x }{ y } for coprime positive integers, what is the value of x + y x+y ?


The answer is 2746.

View wiki
Ivan Molina N by Ivan Molina N , 28, Colombia

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

4 solutions

Marta Reece
Jun 23, 2017

Semi-perimeter s = 1 2 ( a + b + c ) = 20 s=\frac12(a+b+c)=20

Area from Heron's formula A = s ( s − a ) ( s − b ) ( s − c ) = 12 35 A=\sqrt{s(s-a)(s-b)(s-c)}=12\sqrt{35}

Radius of incircle r = A s = 3 5 35 r=\frac As=\frac35\sqrt{35}

Radius of circumcircle R = a b c 4 A = 143 35 105 R=\frac{abc}{4A}=\frac{143\sqrt{35}}{105}

I O ‾ \overline{IO} , horizontal (parallel to A B ‾ \overline{AB} ) component calculation:

A B ‾ = 16 , A D ‾ = 7 , F O ‾ = D E ‾ = 16 2 − 7 = 1 \overline{AB}=16, \overline{AD}=7, \overline{FO}=\overline{DE}=\frac{16}2-7=1

I O ‾ \overline{IO} , vertical (perpendicular to A B ‾ \overline{AB} ) component calculation:

O E ‾ = R 2 − 8 2 , I F ‾ = r − O E ‾ \overline{OE}=\sqrt{R^2-8^2}, \overline{IF}=r-\overline{OE}

I O ‾ 2 = I F ‾ 2 + F O ‾ 2 \overline{IO}^2=\overline{IF}^2+\overline{FO}^2

I O ‾ 2 = ( 3 5 35 − 35 ( 143 105 ) 2 − 64 ) 2 + 1 = 2431 315 \overline{IO}^2=\left(\frac35\sqrt{35}-\sqrt{35\left(\frac{143}{105}\right)^2-64}\right)^2+1=\dfrac{2431}{315}

Answer = 2746 =\boxed{2746}

1 Helpful 0 Interesting 1 Brilliant 0 Confused
Pi Han Goh
Mar 29, 2015

By Euler's Theorem of geometry, we have I O ‾ 2 = R ( R − 2 r ) \overline{IO} ^2 = R(R - 2r) where R R and r r denote the circumradius of the large circle and inradius of the triangle respectively.

The formula for the circumradius for sides p , q , r p,q,r is

p q r 2 ( p 2 q 2 + p 2 r 2 + q 2 r 2 ) − p 4 − q 4 − r 4 \frac {pqr}{ \sqrt{2(p^2 q^2 + p^2 r^2 +q^2 r^2) - p^4 - q^4 - r^4 } }

Substitute p = 11 , q = 13 , r = 16 p = 11,q=13,r=16

And apply the rule for inradius: Area of triangle = r × semiperimeter \text{Area of triangle} = r \times \text{ semiperimeter}

The area of triangle can be easily found using Heron's formula, substitute everything inside the desired equation, we get 2431 315 \frac {2431}{315} , thus our answer is 2746 \boxed{2746} .

2 Helpful 0 Interesting 0 Brilliant 0 Confused

I did it without Euler's Theorem first, but I did use the formulas for inradius and circumradius.

Marta Reece - 3 years, 11 months ago

Log in to reply

If you didn't know about (or apply) the equation (IO)^2 = R(R-2r), then how did you solve this question? Or more precisely, how do you determine the answer based on R and r alone?

Pi Han Goh - 3 years, 11 months ago

Log in to reply

See solution. (I did find the formula and used it to check my answer before submitting it, but did not know it originally. My geometry education is limited to high school, now half a century old, and even that was not in English. There are many formulas I do without.)

Marta Reece - 3 years, 11 months ago

Log in to reply

@Marta Reece – Ah, yes. I believed that's how Euler's theorem was derived.

haha, half a century old. I must over a quarter century old.

Pi Han Goh - 3 years, 11 months ago
Fletcher Mattox
Sep 3, 2020 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
 
from shapes import *
from Find_fraction import find_fraction
from fractions import Fraction

a, b, c = 11, 13, 16

A = Point(0, 0)
B = Point(b, 0)

circleA = Circle(A, a)
circleB = Circle(B, c)
C = circleA.intersect_circle(circleB)[1]

t = Triangle(A, B, C)
I = t.incenter()
O = t.circumcenter()

dist = distance(I, O)
d2 = dist**2
f = find_fraction(d2, 1e-9)
print(f.numerator + f.denominator)


1
 
2746

0 Helpful 0 Interesting 0 Brilliant 0 Confused

U s i n g n o r m a l s y m b o l s . a = 11 , b = 13 c = 16. Δ = 1 4 ∗ ( a + b + c ) ∗ ( − a + b + c ) ∗ ( a − b + c ) ∗ ( a + b − c ) = 12 35 . R = a b c 4 ∗ Δ R = 11 ∗ 13 ∗ 16 48 ∗ 35 = 11 ∗ 13 3 ∗ 35 . r = Δ 1 2 ∗ ( a + b + c ) . r = 12 35 1 2 ∗ 40 = 3 35 20 . B y E u l e r ′ s T h e o r e m o f g e o m e t r y , I O 2 = R ∗ ( R − 2 r ) . I O 2 = 11 ∗ 13 3 ∗ 35 ∗ ( 11 ∗ 13 3 ∗ 35 − 2 ∗ 3 35 20 ) . I O 2 = 143 105 ∗ 17 3 = 2431 315 = p q . p + q = 2746. Using ~normal~symbols.\\ a=11,~~b=13~~c=16.\\ ~~~\\ \Delta~=\frac 1 4 *\sqrt{(a+b+c)*(- a+b+c)*(a- b+c)*(a+b-c)}=12\sqrt{35}.\\ ~~~\\ R=\dfrac{abc}{4*\Delta}\\ R=\dfrac{11*13*16}{48*\sqrt{35}}=\dfrac{11*13}{3*\sqrt{35}}.\\ ~~~\\ r =\dfrac{\Delta}{\frac 1 2 *(a+b+c)}.\\ r=\dfrac{12\sqrt{35}}{\frac 1 2 *40}=\dfrac{3\sqrt{35}}{20}.\\ ~~~\\ By~ Euler's~ Theorem~ of~ geometry~~~,IO^2=R*(R-2r).\\ IO^2= \dfrac{11*13}{3*\sqrt{35}}* \left (\dfrac{11*13}{3*\sqrt{35}}-2*\dfrac{3\sqrt{35}}{20}\right ).\\ IO^2=\dfrac{143}{105}*\dfrac{17} 3=\dfrac{2431}{315}=\dfrac p q.\\ ~~~\\ p+q=\Large~~~\color{#D61F06}{2746}.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...