Let's Do Geometry The Complex Way!
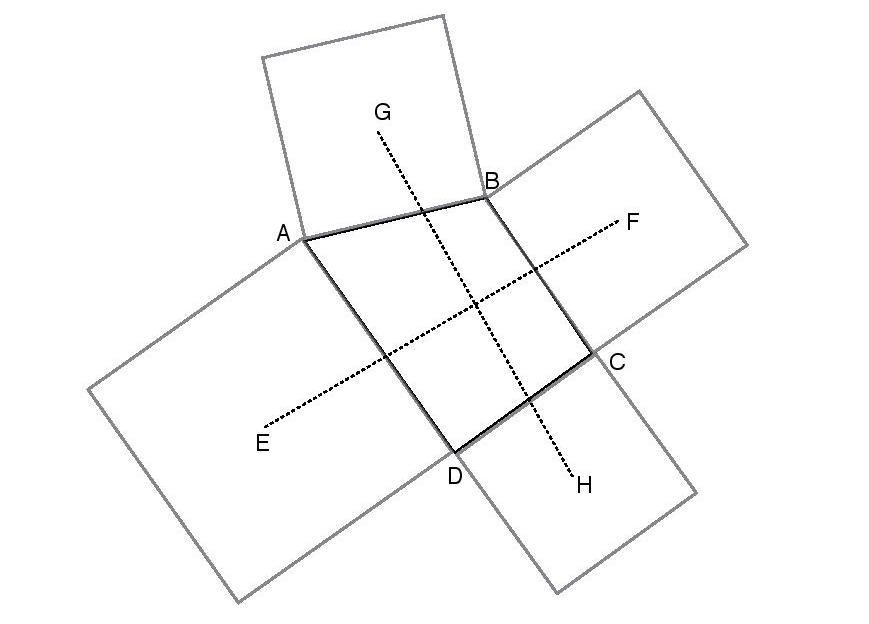
Consider a quadrilateral A B C D with all distinct sides as shown above. Squares are constructed on each of its sides as shown in the figure above. Suppose E , F , G and H be the centres of these squares.
Let r = length ( E F ) length ( G H ) and let 0 ∘ ≤ θ ≤ 9 0 ∘ denote the angle (in degrees) between the lines G H and E F .
Find the value of r + θ .
Bonus : For those who know the result already try doing it in a different way(probably by using Complex Numbers!)
The answer is 91.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
This result is known as van Aubel's theorem .
You might want to remove the image shown. "It strongly suggests" that the answer is 91.
The problem can be solved only with logic also. Since this is true for all quadrilateral, the only possible answer is 90 and ratio as 1.
How do we prove that EF is perpendicular to, say BC? I understood everything else. And thank you so much for the book! I'll read it when my exams end!
Log in to reply
EF might not be necessarily perpendicular to BC. quadrilateral ABCD is an arbitrary quadrilateral and not specifically a rectangle( In which case we can say that EF perpendicular to BC). I am sorry but I didn't exactly get your question. Why exactly do you think that BC shall be perpendicular to EF?
Log in to reply
In your solution, you said that iz is perpendicular to z.
Log in to reply
@Saurabh Chaturvedi – Let z = r e i θ (Here r = ∣ z ∣ )
We know i = e i 2 π
Therefore i z = r e i ( θ + 2 π )
From the above we can infer that if a r g ( z ) = θ then a r g ( i z ) = θ + 2 π implying that, when z is rotated by 9 0 ∘ in the anti-clockwise direction we get i z .
Therefor z is perpendicular to i z (As a r g ( i z ) − a r g ( z ) = 2 π )
Hope this will help you out. If you still have any other doubt regarding the solution do not hesitate to ask.
Log in to reply
@Miraj Shah – I know this stuff. What I am asking is that, if EF is not necessarily perpendicular to BC, how can we write F as 2a + b +ib?
I just assumed the squares are equal. Therefore, their ratio is 1 and the angle formed is 90. LOL HAHAHA
Ya! That's ok for solving the problem for points and levelling up! But the basic idea of posting the question was to show how complex numbers can be used to solve a purely geometric problem purely algebraically! Try proving the theorem for a general quadrilateral and then probably you will be able to appreciate the beauty of the question and moreover it's solution from an algebraic point of view.
P.S. : Do read the book from which the problem has been picked up. It's really very good. The link to that book is given at the end of the first solution.
I remember Napoleon's theorem and applied it here.. How lucky I am!
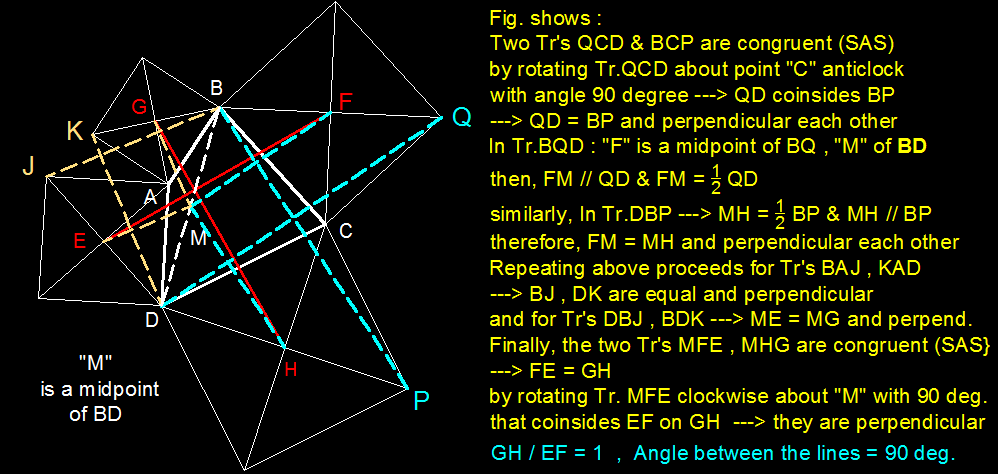
Let 2 a , 2 b , 2 c , 2 d represent the complex numbers running along the edges of the square A B C D .Since these complex numbers form a closed path therefore,
a + b + c + d = 0 .... ( 1 )
Let A (refer this point in the diagram of the question) be the origin. We know that if z represents a complex number then i z represents another complex number with the same magnitude as z rotated by an angle 9 0 ∘ in the anti-clockwise direction with respect to z . Using this analysis we can represent the positions of the centres of the squares as follows:
G ≡ a + i a
F ≡ 2 a + b + i b
H ≡ 2 a + 2 b + c + i c
E ≡ 2 a + 2 b + 2 c + d + i d
Now, let the complex number from G to H be z 1 . Therefore z 1 = a + 2 b + c + i ( c − a ) and ∣ z 1 ∣ = l e n g t h ( G H )
Also, let the complex number from F to E be z 2 . Therefore z 2 = b + 2 c + d + i ( d − b ) and ∣ z 2 ∣ = l e n g t h ( F E ) .
It's easy to observe that z 1 = i z 2
(The above statement can be verified as follows: z 2 + i z 1 = ( a + b + c + d ) + i ( a + b + c + d ) = 0 ⇒ z 2 = − i z 1 ⇒ z 1 = i z 2 )
This means:
z 1 is z 2 rotated by 9 0 ∘ ⇒ θ = 9 0 ∘
∣ z 1 ∣ = ∣ z 2 ∣ ⇒ l ( F E ) l ( G H ) = 1
This problem is from a wonderful book Visual Complex Analysis By Tristan Needham