A New Flag?

Geometry Level 2

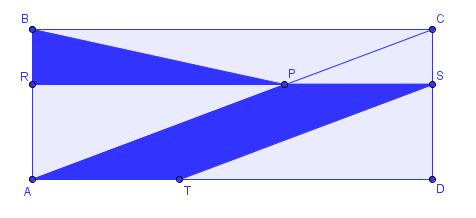
$ABCD$ is a rectangle and $P$ is any point on $AC$ (except $A$ and $C$ ). Through $P$ is plotted a line parallel to $BC$ which cuts $AB$ and $DC$ at $R$ and $S$ , respectively. Also, through $S$ is plotted a line parallel to $AC$ which cuts $AD$ at $T$ .

Find $\dfrac{\text{Area }TSPA}{\text{Area } PRB}$ .

The answer is 2.0.

3 solutions

Ahmad Saad
Apr 22, 2016

Relevant wiki: Length and Area - Composite Figures

$\begin{aligned} \text{Area}|TSPA| &=& (KM) (1-K)N = K(1-K)MN \\ \text{Area}|PRB| &=&\dfrac12 KN(1-k) M = \dfrac12 K(1-K) MN \end{aligned}$

Taking their ratio gives the desired answer of $\boxed2$ .

Nice solution! So for any point P on AC the solution is true, isn't it? No my question is what would happen if P converges to C or A?

Mahabubul Islam - 5 years, 1 month ago

Degenerates figures

Paola Ramírez - 5 years, 1 month ago

I am not clear by your answer!

Mahabubul Islam - 5 years, 1 month ago

@Mahabubul Islam – If $P$ lies on $C$ , then $\triangle BPR$ will be equal to line $BC$ (when $P$ lies on $\triangle BPR$ is equal to $AB$ ) and $TSPA$ will be equal to $AC$ . So both figures will be a line and its area $0$ , $\therefore$ the ratio will be indeterminate.

Paola Ramírez - 5 years, 1 month ago

Patience Patience
May 2, 2016

=sd at/(0.5rp rb) , if p middle ac, rp= at, and sd=rb >>>>>>> soultion is 2

A Former Brilliant Member
Apr 22, 2016

Slightly implicit solution: from the formulation, deduce/infer the answer does not depend on the lengths of the objects. For the particular case of ABCD as a square and P in its center, the answer is quite intuitive. Generalise.

How did you get the generalization?

Paola Ramírez - 5 years, 1 month ago

I meant "the answer for a particular case is probably right for every case", so I just reduced the problem to the case where $A B = A D$ and $A P = P C$ and figured it was the general answer.

A Former Brilliant Member - 5 years, 1 month ago

A New Flag?

The answer is 2.0.

3 solutions

0 pending reports