Paralellbomb

Let $x$ be one side length of the parallelogram in cm. Since the perimeter of the paralellogram is $50$ cm, the other side length is $25-x$ cm.

Let $h$ be the height of the paralellogram with respect to the base of length $x$ . Since the area of the parellogram is $50$ cm $^2$ , $h=\frac{50}{x}$ cm.

We have $(25-x)\cdot \sin\left(\frac{\pi}{6}\right)=\frac{50}{x}$ . Multiplying by $2x$ on both sides, we find $25x-x^2=100$ , so $(x-5)(x-20)=0$ . Then $x=5$ or $x=20$ . In either case, the dimensions of the parallelogram are $5$ cm and $20$ cm.

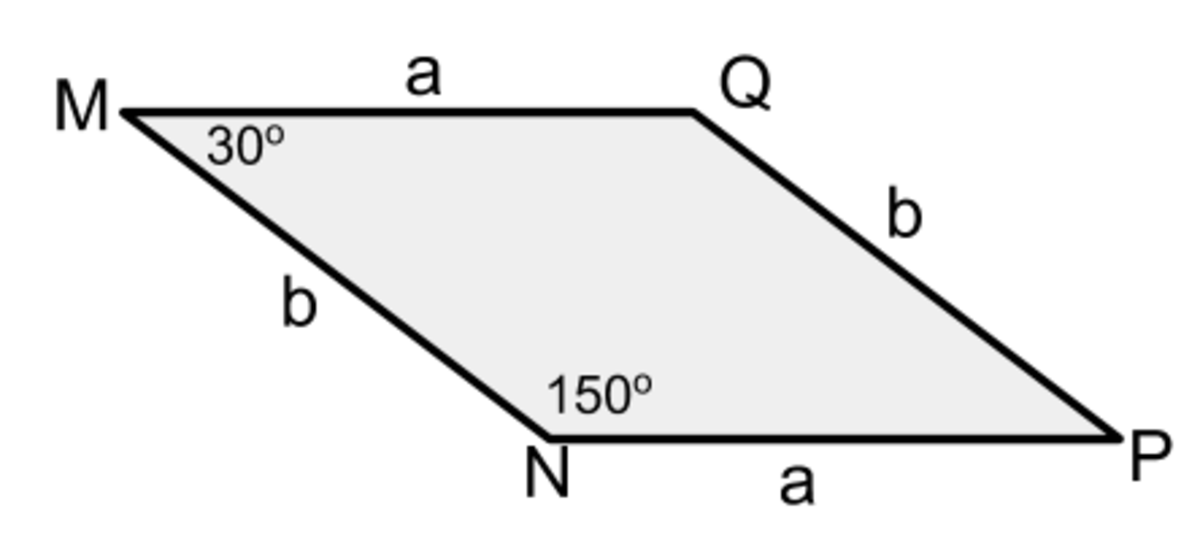
Let a represent the length of one side and let b represent the length of the other side of the parallelogram. You then have a pair of sides of length a and a pair of sides of length b as shown below.

Since you are given the perimeter of 50 you have 2(a+b) = 50.

You are given that one angle is 30 degrees (angle NMQ below) and can determine angle MNP is 150 degrees because MNP and NMQ are supplementary.

Drop a perpendicular from point M to point R and extend segment PN to point R (shown below). Angle MNR is supplementary to angle MNP so angle MNR = 30. This creates 30-60-90 triangle MNR. Through properties of 30-60-90 MR is $\frac{1}{2}$ b.

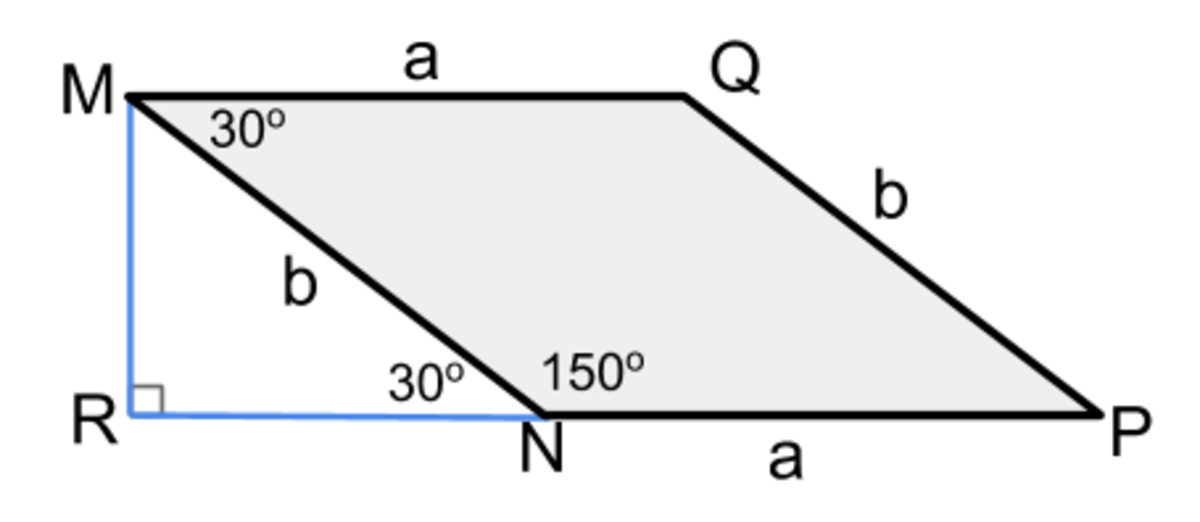
MR is also the height of the parallelogram which gives the equation $\frac{1}{2}$ ba = 50. (Area of 50 was given) .

Solving for a you get a = $\frac{100}{b}$

Substituting for a in 2(a+b)=50 gets you 2( $\frac{100}{b}$ +b)=50

2( $\frac{100}{b}$ +b)=50

$\frac{100}{b}$ + b = 25

100 + b^2 = 25b

b^2 - 25b + 100 = 0

(b - 5)(b-20) = 0

So b is either 5cm or 20cm making a either 20cm or 5cm respectfully. Either way the dimensions are 5cm and 20 cm.