Spinning A Cone

Geometry Level 3

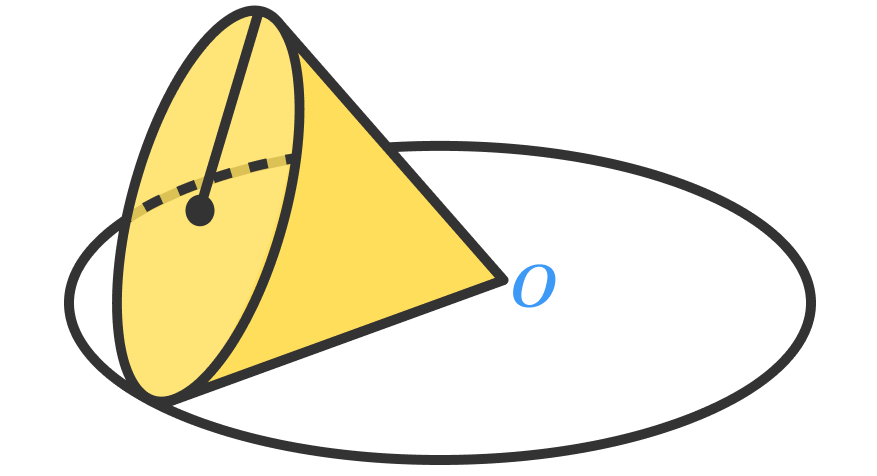
In the picture above, a cone with radius 6cm rolled inside a big circle. It spun around 3 times until it reached the starting point. If the surface area of the cone is A π , A\pi, what is A ? A?


The answer is 144.

View wiki
Shintaro Inaba by Shintaro Inaba , 17, Japan

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Recall that the perimeter of a circle is 2 π r 2\pi r and surface area of a cone is π r ( r + s ) \pi r(r + s) , where s s denote the slant height of this cone.

3 times the perimeter of the base of the cone: 3 × 2 π r = 3 × 2 π × 6 = 36 π 3\times 2 \pi r = 3 \times 2 \pi \times6 = 36 \pi .

So the perimeter/circumference of the big circle is 36 π 36 \pi , let R R denote the radius of the big circle, then 36 π = 2 π R 36 \pi = 2 \pi R or R = 18 R = 18 .

Since the radius of the big circle is equivalent to the slant height of the cone, then s = R = 18 s = R = 18 .

Thus the total surface area of the cone is π r ( r + s ) = π ( 6 ) ( 6 + 18 ) = 3.14 × 6 × 24 ≈ 452.16 \pi r (r + s) = \pi (6)(6 + 18) = 3.14 \times 6 \times24 \approx 452.16 .

8 Helpful 0 Interesting 0 Brilliant 0 Confused

Wait, if the cone rotates three times, then we have to divide by three, haven't we?

The circumference of the cone base is 2 ⋅ π ⋅ 6 = 12 π 2 \cdot \pi \cdot 6 = 12 \pi . Now it makes 3 3 complete rotations, thus the circumference of the big circle is 12 3 π = 4 π ⇒ R = s = 2 \frac{12}{3} \pi = 4 \pi \Rightarrow R = s = 2 .

Where's my mistake?

Patrick Engelmann - 5 years, 2 months ago

Log in to reply

36pi is the circumference of the big circle, not the cone.

A Former Brilliant Member - 5 years, 2 months ago

Log in to reply

I have misunderstood the problem. I thought that the cone will do exactly one rotation in the big circle. But you are supposed to assume that the cone will do 3 rotations in the circle.

Patrick Engelmann - 5 years, 2 months ago

Log in to reply

@Patrick Engelmann – No need to assume. We are told the cone rotates three times to complete the large circle. Cheers.

A Former Brilliant Member - 5 years, 2 months ago

Log in to reply

@A Former Brilliant Member – Yes, but we are not told that the cone will rotate exactly three times in the big circle. It can also do one rotation in the big circle and after three rotation it will be at the starting point again. Does it spin around itself 3 times or around the big circle 3 times? I dont think it's very clear and the hardest part of this problem is to decrypt what you're actually supposed to do.

Patrick Engelmann - 5 years, 2 months ago

Log in to reply

@Patrick Engelmann – "It spun around 3 times until it reached the starting point."

A Former Brilliant Member - 5 years, 2 months ago

Log in to reply

@A Former Brilliant Member – Indeed, it spun around what? Itself (what are you supposed to assume) or maybe around the big cricle. Then you still don't know how many rotations the cone actually does, if it spins around the big circle. It could do one, two, three, 400 rotations for the 3 spins around the big circle.

Patrick Engelmann - 5 years, 2 months ago

@Patrick Engelmann – If you feel this question is misleading, feel free to report to the staff.

A Former Brilliant Member - 5 years, 2 months ago

You shouldn't divide by three. In fact you should multiply by three.

A Former Brilliant Member - 5 years, 2 months ago
J Chaturvedi
Mar 16, 2016

As the cone has to be rolled 3 times to cover the circle, the circumference of circle is 3 times that of the base of cone, which means its radius is 3 times that of cone I.e. 6×3=18 and similarly, the Surface area of curved surface of cone would be one third of the area of circle i. e. π×18×18/3=108π. The area of base of the cone is π ×6×6=36π. Therefore, total area=108π+36π=144π.

3 Helpful 0 Interesting 0 Brilliant 0 Confused

yes the only reason we need to find the circumference of the large circle is because we need to know the slant of the cone and that is the same as the radius of the large circle.

A Former Brilliant Member - 5 years, 2 months ago
Teleanu Florin
Mar 17, 2016

I Think that the solution Is wrong by the assumption that the circumference of the big circle is 3 times that of the base. This problem Is very similar with the 2 coins problem. If a small circle spins 3 times around the big one, this means that the radius of the former Is 2 times smaller, not 3. In my opinion, the number of spins Is equal to R/r minus the cosinus of the angle between the circles with the given radius. R/r - cos(a) =3 and substituing cos(a)=r/R, we get that R=19,81. So the area will Be 6 3.14 19.81=373.34 . I would like to hear further opinion.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

If you think the answer is wrong, click the report button.

Pi Han Goh - 5 years, 3 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...