The Astute Ant
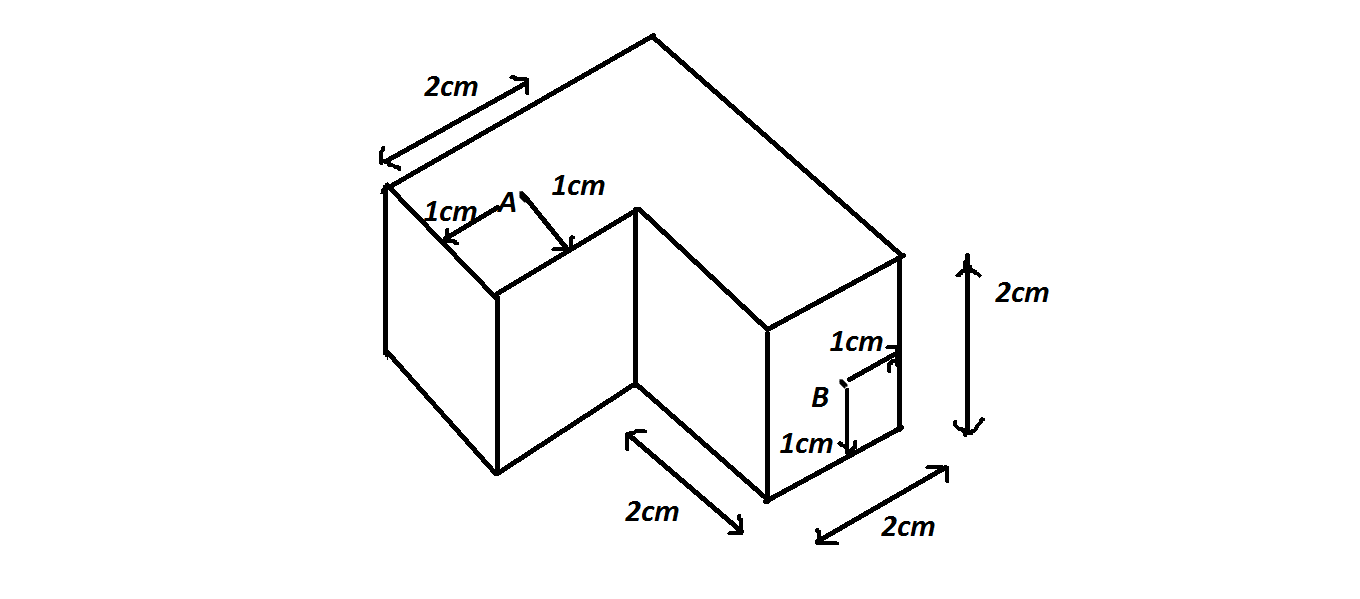
In the figure we are shown a L-shaped block, with side-lengths 2 cm .
An ant initially at point A , wants to go to point B , along the shortest path possible along the surface of the block.
If the length of the shortest path can be written as m + n where m and n are square-free positive integers, find m + n .
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Great question! A nice variation of the standard cube/cuboid problem.
Note: The image could be improved by making it clearer (maybe in another color) where A and B are. I will try and upload an image later on.
Log in to reply
Thank you, sir.
Yes I found this question appealing because the direct unfolding strategy does not work at first here.
Yes, it would be very helpful of you to upload an image, when you get time.
Log in to reply
Hi,are you planning to take admission in the Indian Statistical Institute?
Log in to reply
@Manish Maharaj – Yes, CMI and ISI are what I am aiming for.
Log in to reply
@Soumava Pal – Just one more doubt.In case of ISI, in the subjective paper,on an average how many problems should one be able to solve to get an interview call?Also,does the interview call also depend on the performance of the student in the objective paper? Thanks
Log in to reply
@Manish Maharaj – As far as I know, one's score on the objective is used to decide if his subjective answer sheet is going to be checked, that is, you require a requisite minimum on the objective paper to get your subjective answer sheet checked, and for the interview call, I think only the subjective marks are considered.
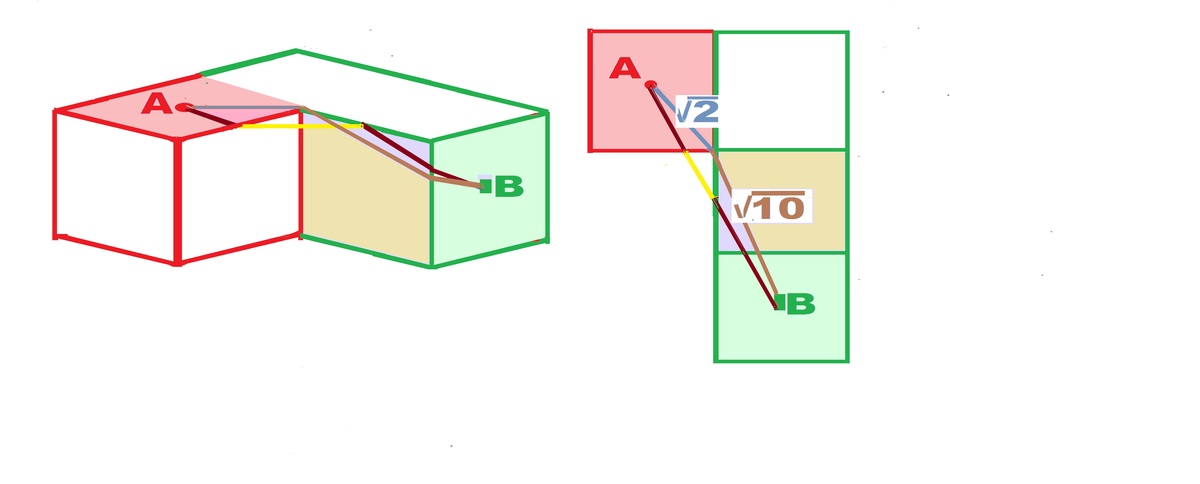 As shown in the sketch, Shortest path is brown+yellow+brown. But yellow is in air. So to clear shortest path
on the surface, the ant has to go diagonally to the corner. This distance is
2
.
Now it is in a position to go on the shortest surface paths. It has to travel one unit down and 2+1=3
units so to say right. But these are legs of the right triangle. So the shortest is the hypotunuse
1
0
.
∴
m
+
n
=
1
2
.
As shown in the sketch, Shortest path is brown+yellow+brown. But yellow is in air. So to clear shortest path
on the surface, the ant has to go diagonally to the corner. This distance is
2
.
Now it is in a position to go on the shortest surface paths. It has to travel one unit down and 2+1=3
units so to say right. But these are legs of the right triangle. So the shortest is the hypotunuse
1
0
.
∴
m
+
n
=
1
2
.
First we observe that to move from A to B , along the surface, the ant has to cross the plane shaded in the following figure.
Now, to cross the plane shown, it has to cross the line P O Q at some point in between P and Q on P O Q .
So we consider the following cases where the ant can cross the line P O Q at X between O and Q , or at O , or at X ′ between O and P .
Case 1
The ant crosses the line P O Q at a point between O and Q , say X .
Now we unfold the part of the block given by C R O K F J I E H Q C so that we can find the straight line distance from X to B , and compare the distance from A to B along X to that along O .
( Note
When we fold the piece above back to it's original form, the ant can actually walk along the path X B though it will not be a straight line, it will undergo a change in it's slope at the two points where it meets the edges. )
Now we see, that in triangle A X B , O is an internal point, and we know that A X + X B > A O + O B , from Dogleg's Rule , so for any point X between O and Q , the total path length is greater than if the ant goes along O .
Case 2
The ant crosses the line P O Q at a point between O and P , say X ′ .
Now we unfold the part of the block given by C R G P F J I K O Q C so that we can find the straight line distance from X to B , and compare the distance from A to B along X ′ to that along O .
Again we see in triangle A X ′ B , O being an internal point, A X ′ + X ′ B > A O + O B by Dogleg's rule again.
So we have to cross the said plane at point O only.
Calculation
We can check that the distance A O + O B is same in both cases. A O = 1 2 + 1 2 = 2 and O B = 3 2 + 1 2 = 1 0 , so that we get m = 2 and n = 1 0 .
Note
The unfolding of the whole block could not be done at the very beginning because in that case the faces O Q H E and O K I E would overlap and the path chalked out for the ant would not be along the surface of the block, it would be a path suspended in air.