A geometry problem by vansh gupta
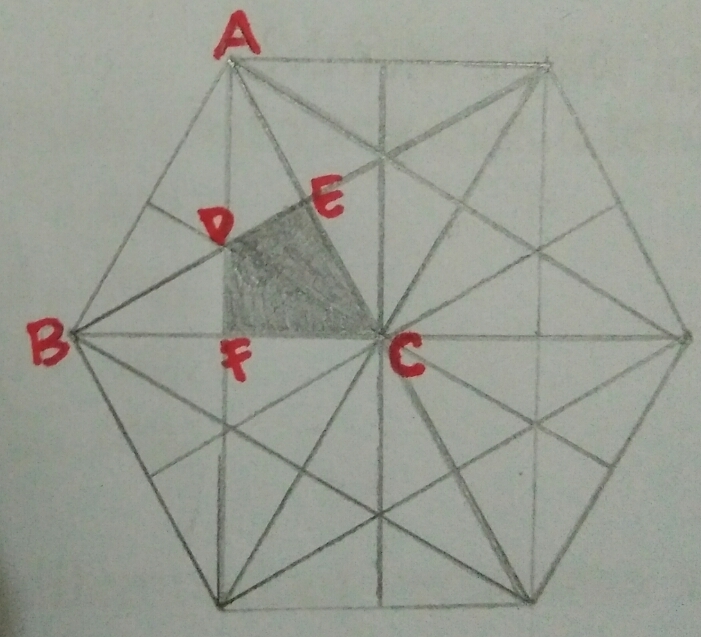
The figure above shows a regular hexagon with area 1.
What is the area of the shaded region?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Very nice illustration!
Pi Han Hoh sir ....thanks
Awesome pics mate
You can split the hexagon into 6 triangles, and split the one that the purple area is into 6 identical triangles, of which the purple area covers two. Therefore, the result is 2/6 or 1/3 of 1/6, or 1/18
As we can see, each equilateral triangle can be made by three kites, and they are all congruent to each other. Since there are six equilateral triangle, we can conclud that R = 1 8 × [ C E D F ] . Then, the area of the shaded region is [ C F D E ] = 1 8 R .
Moderator note:
This is a very common technique seen in competitions where what's potentially a symmetrical figure has line segments missing. Adding line segments to make the figure actually symmetrical then makes it much simpler to see the how the areas of the figure relate.
Nice! Splitting the hexagon into (lots of) congruent triangles makes easy to find the area of the shaded region.
I don't see how three rhombuses make an equilateral triangle. Do you mean that each equilateral triangle is made by three kites?
Log in to reply
Yes. Actually, it's not hard to notice that the hexagon can be splitted into lots of kites.
By drawing the diagonal through the marked quadrilateral, one can see that the right triangle that is half of the equilateral triangle is made up of 3 identical small right triangles. Hence, the marked area is 3 2 of the right triangle that is half of the equilateral triangle and therefore has the area 1 8 1 R .
It has to be something less than 1 2 1 of R, and 1 8 1 is the only choice there is.
The shaded diamond, can also be seen as 1/3 of its equilateral triangle that is 1/6 of the original hexagon.
Why it has to be less of than 1/12 of R?
Log in to reply
There are six equilateral triangles that make up a hexagon, and the marked area is less than half of one. But, in any case, by drawing the diagonal through the marked quadrilateral, one can see that the right triangle that is half of the equilateral triangle is made up of 3 identical small right triangles. Hence, the marked area is 3 2 of the right triangle that is half of the equilateral triangle, and therefore has the area 1 8 1 R
Log in to reply
Thanks. I've added that to the solution.
Alternatively, we can see that the (relevant) lines are medians of the equilateral triangle, so the point of intersection is the centroid, and the region is 6 2 of the equilateral triangle.
Log in to reply
@Calvin Lin – Quality solutions is what Brilliant.org needs.
1/24 is less than 1/12
Log in to reply
We updated the options after this solution was posted to make them more reasonable. Previously, the options were 1/3, 1/6, 1/12, and 1/18. It is pretty clear that 1/3, 1/6 and 1/12 were not valid, so we replaced them.