Triforce Triangle?
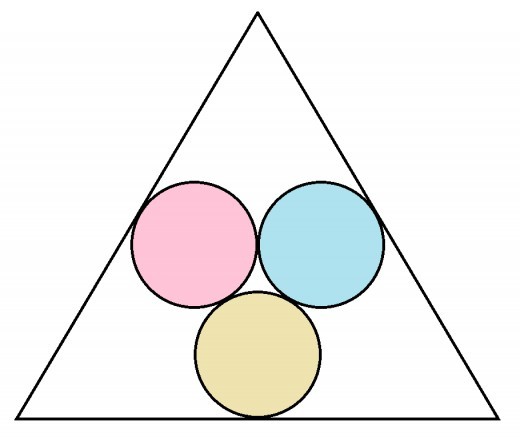
Three circles are inscribed within an equilateral triangle such that they are tangent to one another and to the midpoint of one edge of the triangle. If each circle has a radius of 1 cm, what is the side length of the triangle in cm?
Give your answer to 3 decimal places.
The answer is 7.464.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
How do you justify the existence of the other 3 circles each having radius 1 cm? It may be trivial, by I didn't get, so, could you explain it in detail?
Log in to reply
@Deeparaj Bhat
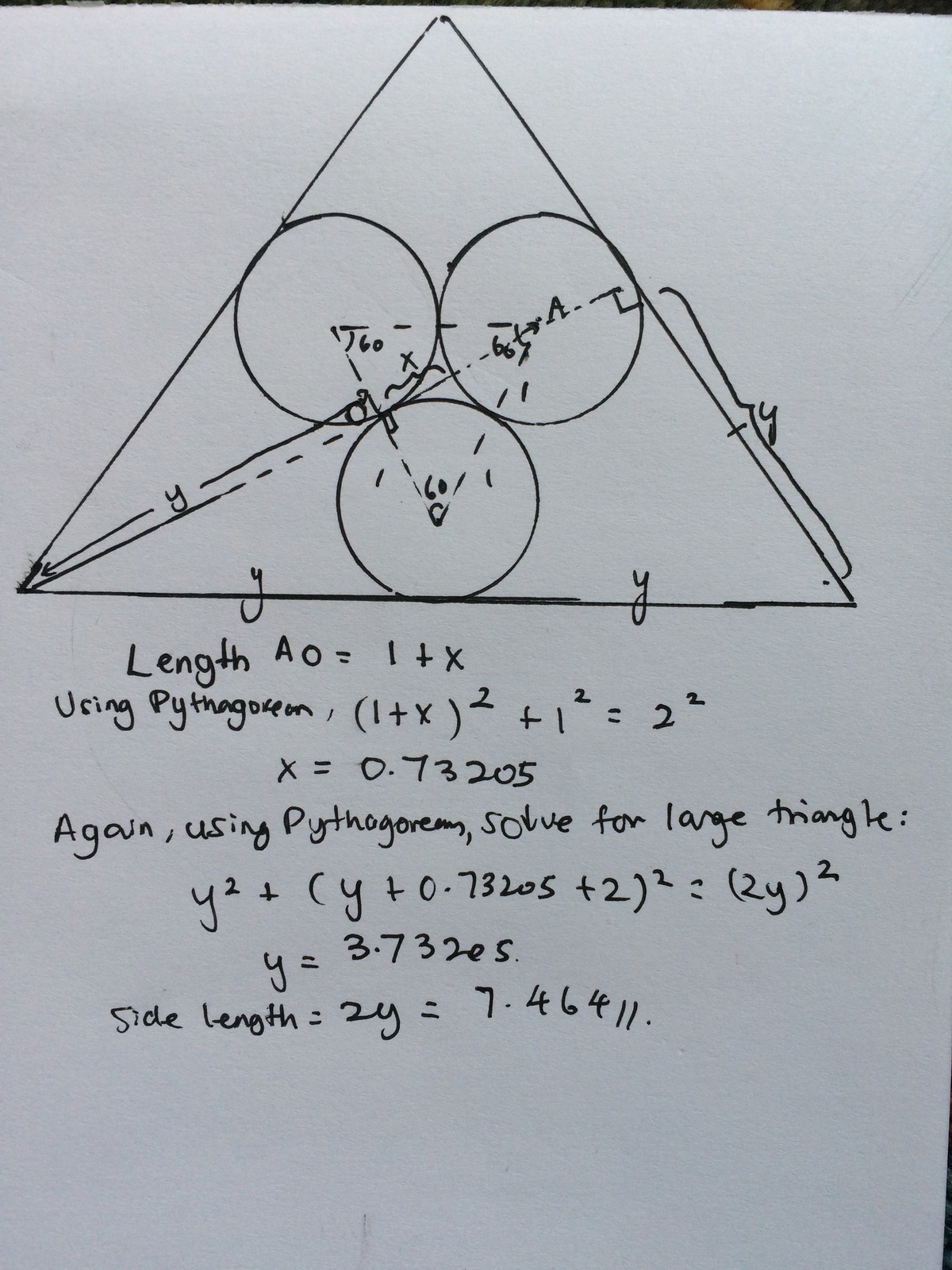
Let the radius of the other three corner circles be x . (The circles will be congruent.)
If we join the centre of each circle with the ones it touches, then four triangles will be formed. The triangle in the centre will be equilateral triangle of side 2 cm. The other three triangles will be isosceles with two sides of length ( x + 1 ) c m and one side 2 cm.
Now consider ∠ A B D in the figure,
∠ A B C + ∠ C B E + ∠ E B D = 1 8 0 °
Putting ∠ A B C = ∠ E B D (Since both the isosceles triangles are congruent) and ∠ C B E = 6 0 °
2 ∠ A B C = 1 2 0 °
∠ A B C = 6 0 ° = ∠ E B D
Then, by the angle sum property of triangle we get that each angle of all the isosceles triangles is 60°.
Thus, we can conclude that all the three isosceles are actually equilateral triangles.
We know the length of one side is 2 cm and the other two ( x + 1 ) c m .
x + 1 = 2
x = 1
Hence we get x ⇒ 1 c m . Therefore the radius of the other three circles will be 1 cm.
Log in to reply
Thanks. I didn't mean to offend you though.
Log in to reply
@A Former Brilliant Member – Welcome! I didn't considered your comment as offensive. Its rather good that you understand every part of the solution.
My solution is along the lines of Yash Jain's, but without adding the additional circles.
The red line segment consists of two radii combined, therefore it has length 2.
Each blue line segment has length 1, and makes an angle of 3 0 ∘ with the horizontal. Its projection on the horizontal (the green line segment) is therefore cos 3 0 ∘ = 2 1 3 .
The total length of green + red + green is therefore 2 1 3 + 2 + 2 1 3 = 2 + 3 . This line segment connects two midpoints of the triangle.
It is well-known that the line segment connecting the midpoints has half of the length of the side parallel to it. Therefore the side of the triangle is 2 ⋅ ( 2 + 3 ) = 4 + 2 3 ≈ 7 . 4 6 4 .
Seriously saying your solution is way better than the other solutions (+1)
visit my youtube channel https://www.youtube.com/channel/UCt2lCfR-9Q-I-Y_a6HLriXw
same is my process
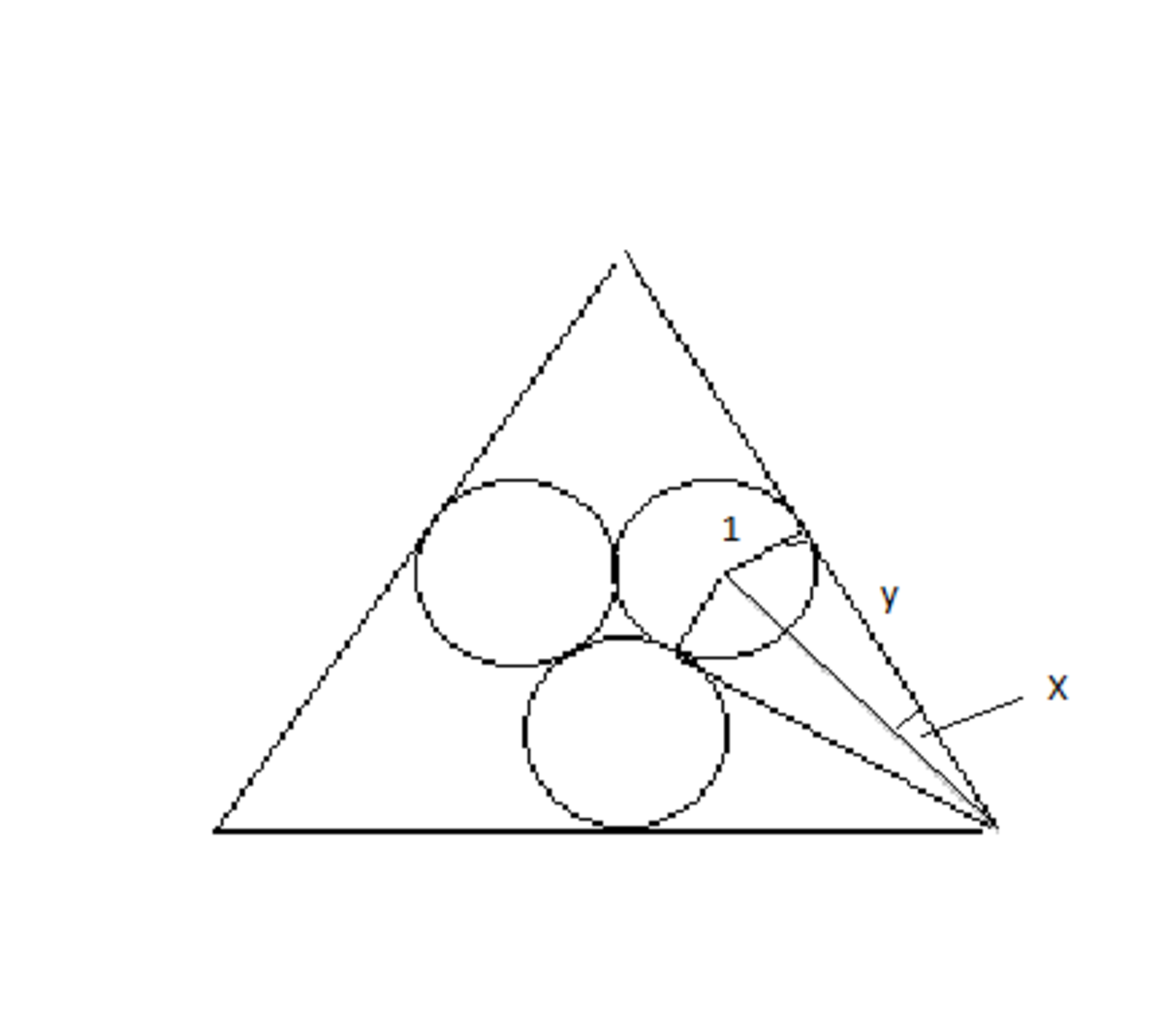 x is the angle from a vertex of triangle to the center of one of the circles.
x is the angle from a vertex of triangle to the center of one of the circles.
x
=
1
5
t a n 1 5 = 1 / y ; y = 3 . 7 3 2
side of triangle = 2 ∗ y = 7 . 4 6 4
Same solution I had......definitely elegant and succinct!
Log in to reply
I wouldn't call it elegant. Succinct... yes, but not elegant. Solved this way makes the question unworthy of Level 4.
smart solution! but letters perusa eludhu.
Log in to reply
My handwriting..
From the top vertex, two tangent go to the red circle. One the left side and the other the angle bisector. They make an angle of 60/2=30. Hence radius/tangent length =Tan(30/2)=Tan15. Implies Tangent length=1/Tan15. But this is only half the sides. So sides=2/Tang15=7.4641.....

Draw three more circles at the corners of the triangle so that they are tangent to the original three and to the sides of the triangle. These new circles also have a radius of 1. Draw the line segments as shown in the figure so that you create a rectangle and two 3 0 ° − 6 0 ° − 9 0 ° triangles.
Note that the angle of the triangle (=60°) gets bisected, making two 30° angles.
tan 3 0 ∘ = 3 1
So,the base of each triangle is of length 3 cm.
The length of each side of the equilateral triangle (in cm) will be ( 3 + 4 + 3 )
Thus, the answer is ⇒ 4 + 2 3 ≈ 7 . 4 6 4