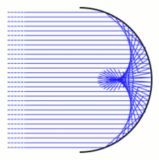
A Heart from Coffee Cup

Geometry Level 3

The caustic appearing on the circular surface with radius $3\text{ cm}$ of this cup of coffee, with a spotlight source on the perimeter, turns out to be a cardioid.

What is the area $\big($ in $\text{cm}^2\big)$ of the region that the cardioid encloses?

The answer is 18.8495559.

3 solutions

David Vreken
Jun 9, 2018

A cardioid is formed by tracing a point of a circle with radius $a$ that is rolled around another circle with the same radius, as shown in the animation below, and has a polar equation of $r = 2a(1 - \cos \theta)$ .

The caustic of a circle with radius $r_c$ with a light source on the perimeter is a cardioid in which $a = \frac{1}{3}r_c$ (see here ). For a coffee cup with a radius of $r_c = 3 \text{ cm}$ , the cardioid formed has an $a$ value of $a = \frac{1}{3} \cdot 3 = 1 \text{ cm}$ .

The area $A$ enclosed by the cardioid is $A = \int_{0}^{2\pi} \frac{1}{2}r^2 d\theta$ $=$ $\int_{0}^{2\pi} \frac{1}{2}(2a(1 - \cos \theta))^2 d\theta$ $=$ $6\pi a^2$ .

Since $a = 1 \text{ cm}$ , the area enclosed by the given cardioid is $A = 6\pi(1)^2 = \boxed{18.8495559 \text{ cm}^2}$ .

It seems almost intuitively right to imagine that the cup has a diameter exactly 3 times the diameter of the smaller circles, but why? Sometimes a cardioid can be a caustic, but one can form different kinds of caustics inside the cup depending on the location of the light source. Let's see...

Yes, there's an explanation for this. Let $\theta\rightarrow 0$ be the angle line $PO$ makes (see Henning's figure) when it is very close to point $F$ . Then let $x \rightarrow 0$ be the approximate value for angles $\angle APO$ , $\angle OPF$ . We know that for triangle $OPA$ , $\; x=\frac{1}{2}\theta$ .
By Law of Sines, we have

$\dfrac { Sin(x) }{ FO } =\dfrac { Sin(\theta +x) }{ OA }$

and so the limit as $\theta \rightarrow 0$ is $\dfrac{OA}{FO}=3$ .

Michael Mendrin - 3 years ago

Yes, there is no a priori reason that I can think of why the light-reflection properties of a caustic should require that the generating circles of the cardioid should lie inside the coffee cup. You can look at my diagram, or else look at my analysis, and see that it is true, but I am not yet convinced that this is an argument that proves the solution.

Mark Hennings - 3 years ago

When I was solving this problem, in my research I read that, "If in the plane there is a light source Z on the perimeter of a circle which is reflecting any ray, then the reflected rays within the circle are tangents of a cardioid" and in the following proof $a$ had to be $\frac{1}{3}r$ , which meant that coffee circle (with radius $r$ ) must span three cardioid generating circles (with radius $a$ ). I took this to be a theorem which I used in my solution. (Perhaps I could have shown more of the proof, but I was trying to be short.)

David Vreken - 3 years ago

@David Vreken – In practice, what often happens is that the light source is some distance away from the cup, so that the rays are almost parallel, in which case one would see a nephroid as the caustic, not a cardioid. And, yet, because the light would be coming from only one direction, one would actually only see one half of a nephroid, which can easily be confused with a cardioid. The difference is that the nephroid would be tangent to the circle in 2 places, not 1.

Michael Mendrin - 3 years ago

@Michael Mendrin – the problem stated that the shape formed is a cardioid, not a nephroid, so there should be no confusion

David Vreken - 3 years ago

@David Vreken – Well, true enough, it does say that. I'm just making a commentary that what we actually see in cups is often confused with a cardioid. I think that parallel light from a non-vertical angle reflecting off a conical cup could produce this? Let me think about that. (edit) ..uh, no, that wouldn't work. Most likely, the light source is pretty close, so what we have is something inbetween a nephroid and a cardioid.

Michael Mendrin - 3 years ago

@David Vreken – The Wikipedia page you reference gives an alternative proof of the result I showed. The fact that $a=r/3$ is a consequence of that analysis, rather than a basic principle. Your presentation gives the impression that the relationship between $a$ and $r$ is obvious, which it is not.

Mark Hennings - 3 years ago

@Mark Hennings – I agree, but isn't the point of any theorem to show a not-so-obvious relationship to shorten a proof? For example, the law of cosines is not an obvious relationship in a triangle, but would you feel the need to prove it every time you wanted to use it in a solution? At what level of difficulty does one have to explain the theorem or just pass it off as obvious? (I've thought about this before when writing solutions to other problems.)

David Vreken - 3 years ago

@David Vreken – When a key result is stated without justification, the result is either obvious (in which case all is well) or else the argument is incomplete.

Mark Hennings - 3 years ago

@Mark Hennings – I see. I adjusted my solution to justify a = r/3 with a link to the proof on the Wikipedia page. I hope that this is a good compromise. Thanks for all your help!

David Vreken - 3 years ago

3x2(pi) = 18.84cm2

Derek Go - 2 years, 11 months ago

Mark Hennings
Jun 2, 2018

We want to find the envelope of the collection of lines $L$ , the first reflections of rays of light emitted from the point $A$ and reflected in the circular boundary.

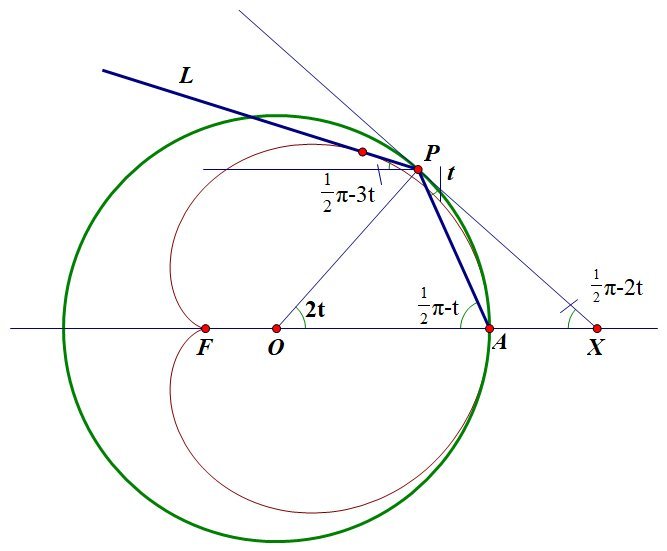
If $\angle POA = 2t$ , then the gradient of the line $L$ is $-\tan(\tfrac12\pi - 3t) = -\cot3t$ . Thus the equation of the line $L$ is $\begin{aligned} y - 3a\sin2t & = \; -\cot3t(x - 3a\cos2t) \\ x\cos3t + y\sin3t & = \; 3a\cos t \end{aligned}$ if the circle has radius $3a$ . The envelope of a family of curves $f(x,y,t) = 0$ is obtained by eliminating $t$ from the pair of equations $f(x,y,t) \; = \; 0 \hspace{2cm} \frac{\partial}{\partial t}f(x,y,t) \; = \; 0$ and so we need to solve the equations $\begin{aligned} x\cos3t + y\sin3t & = \; 3a\cos t \\ x\sin3t - y\cos3t & = \; a\sin t \end{aligned}$ and hence $x \; = \; 3a\cos t \cos3t + a\sin t\sin3t \hspace{2cm} y \; = \; 3a\cos t \sin3t - a\sin t \cos3t$ so that $x+a \; = \; 2a(1 + \cos2t)\cos2t \hspace{2cm} y \; = \; 2a(1 + \cos2t)\sin2t$ Thus the desired envelope is the cardioid $r \; = \; 2a(1 + \cos \theta)$ with polar origin at the point $F\;(-a,0)$ . Note that the line from the polar origin $F$ to the point of contact of the cardioid with the line $L$ is parallel to $OP$ .

The area of this cardioid is $6\pi a^2$ . For this problem, $a = 1$ cm, and so the area is $\boxed{6\pi}$ cm ${}^2$ .

Mark, can you please tell me what do you use for the beautiful graphics?

Michael Mendrin - 3 years ago

Geometer's Sketchpad. I particularly like the way it can be use to draw loci, like the cardioid here, using a single command.

Mark Hennings - 3 years ago

Michael Mendrin
May 31, 2018

You really should mention that this is a caustic from a spot light source on the perimeter of the cup. This isn't obvious from the photograph. Or maybe that's part of the puzzle?

@Michael Mendrin I agree.....even I was confused in my first attempt......!!

Aaghaz Mahajan - 3 years ago

Thank you for reminding. I have edited the question accordingly.

Brian Lie - 3 years ago

Thanks. I see that this problem has been edited.

In the future, if you have concerns about a problem's wording/clarity/etc., you can report the problem. See how here .

Brilliant Mathematics Staff - 3 years ago

Do you mean cycloid instead of caustic?

Bill Weihmiller - 3 years ago

A Heart from Coffee Cup

The answer is 18.8495559.

3 solutions

0 pending reports