Honeycomb Resistance
First Honeybee : I am bored of making my comb with the normal matter that we use. Can't we use anything else?
Second Honeybee : Yeah, we can, I saw some humans carrying a piece of wire.
And finally, after they acquired a piece of wire, they built their usual honeycomb as shown below with the piece of wire. Their job is finished now. Our job is to find out the equivalent resistance between point A and point B.
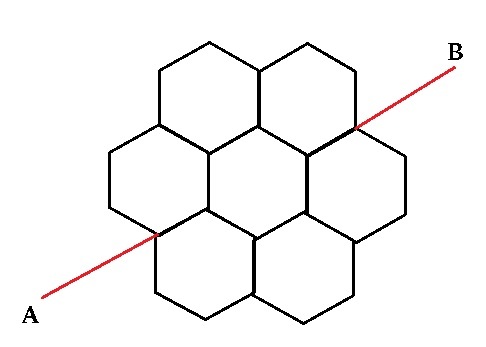
Each black line segment in the above figure represents a resistor of 1 Ω .
If the equivalent resistance is R . Then enter the value of 1 0 0 0 0 0 R .
This question is part of the set Platonic Electricity .
The answer is 191250.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
First step: Reduce the solution to an easy figure, which can help us analyze the circuit easily
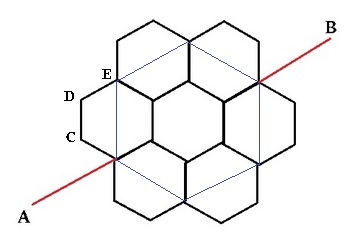
In the above figure, the blue line represents the equivalent resistance of the outer half of each hexagon through which it is drawn.
For instance each side = 1 Ω and therefore R A C D E = R A E = 3 Ω .
After the reduction the figure looks something like this:
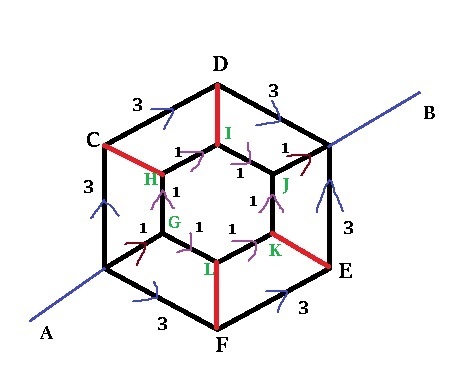
The r e d line shows the dead resistance by the principal of equipotential points in the circuit.
In the outer Hexagon A , C , D , B , F , E the b l u e arrow shows the flow of current, and while flowing through the two branches the current never divides as the nodes which are in the path are connected by dead resistances.
For the inner hexagon the current first enters through the branch ( A G ) and then divides equally at node G , but after that it never divides and rather joins at node J .
So, total R = o u t e r h e x a g o n A C D B ( 3 + 3 + 3 ) p a r a l l e l t o A F E B ( 3 + 3 + 3 ) p a r a l l e l t o i n n e r c i r c u i t ( 1 + i n n e r h e x a g o n 2 3 + 1 )
R = o u t e r h e x a g o n ( 9 ) p a r a l l e l t o ( 9 ) p a r a l l e l t o i n n e r h e x a g o n ( 2 7 )
R = 3 2 6 3 = 1 . 9 6 8 7 5
1 0 0 0 0 0 R = 1 9 6 8 7 5
@Rishabh Tiwari , check this, if there is something left unexplained.
Log in to reply
Sorry for late reply,
Nothing left unexplained; its perfect!!!!
I got just one word for this solution :
" M I N D − B L O W I N G ! ! ! " , really bro Awesome solution!!!
T i w a r i ′ s A l w a y s R o c k s ! ;-) @Abhay Tiwari .!
@VIneEt PaHurKar , What do you think?
Log in to reply
Ha ha, that's flattering on both sides =D.
Log in to reply
@Abhay Tiwari – Haaaa;-) just loved it! Your number theory problems are also awesome I Solved a few of them!
Log in to reply
@Rishabh Tiwari – Great, thanks for your feedback. What should I say. Thanks a lot for your comments. :)
Dear Sir, I am sorry, but your answer is wrong. Actually the red line resistances are not dead. You can easily check it for instance by calculating the potential difference between points C and H following your point of view. You wouldn't get "0" at all. .
Please explain me how you used symmetry to find dead resistance.
How did you conclude that the red ones are dead? Please explain.
How can you say those resistances are dead? they are not i verified using Kirchoff's law
How do you know those points are of equal potential?
I don't know to write a good solution using latex but here I can provide a ' hint ' .
"Consider the middle hexagon, here , by symmetry, no current will flow in the branches connecting its top two vertices & bottom two vertices to the other Hexagons ! " Hence we disconnect those branches & our circuit simplifies to three resistances of 9 , 9 & 2 7 ohms connected in parallel ! Solving this we get, R= 3 2 6 3 ; Hence, final answer is 1 0 0 0 0 0 R = 1 9 6 8 7 5 .
@Swapnil Das , please comment & post a good solution.Thank you.
This was quick :), your solution is correct but you need to elaborate it.
Log in to reply
Exactly, but I don't know how to present it using latex.
Log in to reply
No problem, spend some time writing some problems or solution and you will get used to it. It's not a big deal. And I will post the solution by the end of tonight. :)
Log in to reply
@Abhay Tiwari – Thank you. I will ,for sure, practice solution writing, btw excited To see your solution :)
Log in to reply
@Rishabh Tiwari – Ha ha, I will try my best to make it interesting.
Let's first rearrange the circuit a bit: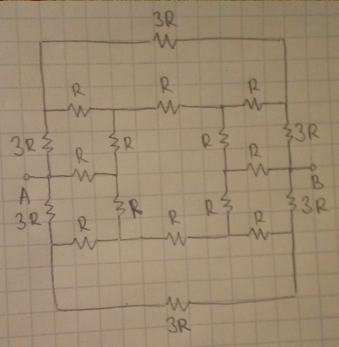 Then we use this:
Then we use this:
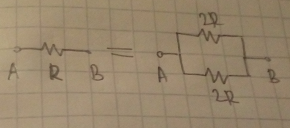 In the rearranged circuit to get this:
In the rearranged circuit to get this:
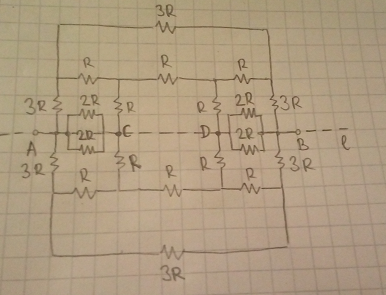 Now, since the circuit is symmetric about line
l
, using the symmetry point-splitting rule, we can split points C and D to get this circuit:
Now, since the circuit is symmetric about line
l
, using the symmetry point-splitting rule, we can split points C and D to get this circuit:
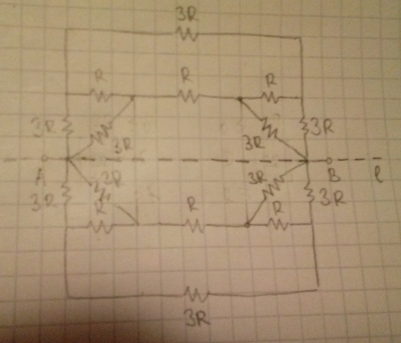 The circuit is still symmetric, but this time it is divided into two equal parts - top and bottom part. Let's take a look at only the top part:
The circuit is still symmetric, but this time it is divided into two equal parts - top and bottom part. Let's take a look at only the top part:
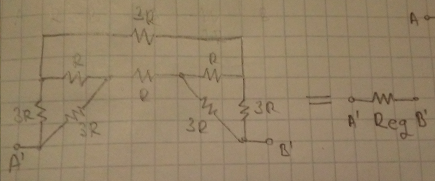 Top part and bottom part have the same equivalent resistance, so the starting circuit can be represented as:
Top part and bottom part have the same equivalent resistance, so the starting circuit can be represented as:
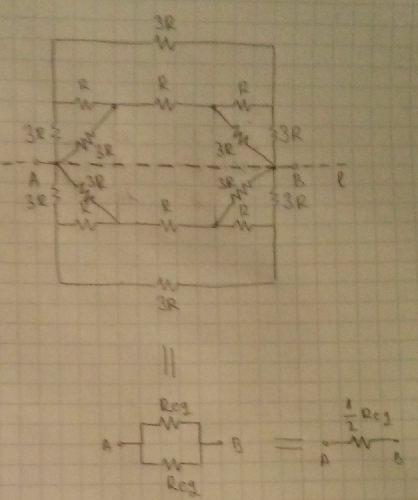 The equivalent resistance of the honeycomb is
2
R
e
q
, so, all we need to do is find
R
e
q
. Let's rearrange this top part of the ciruit:
The equivalent resistance of the honeycomb is
2
R
e
q
, so, all we need to do is find
R
e
q
. Let's rearrange this top part of the ciruit:
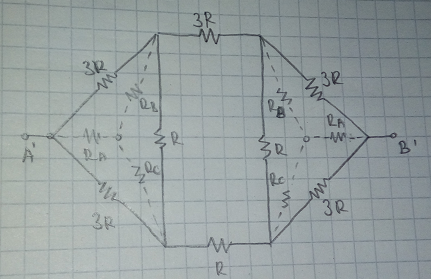 By applying the triangle-to-star transformation rule, we get that:
By applying the triangle-to-star transformation rule, we get that:
R A = 3 R + 3 R + R 3 R × 3 R = 7 9 R R B = R C = 3 R + 3 R + R 3 R × R = 7 3 R
After transformation and another rearrangment, we get this final circuit: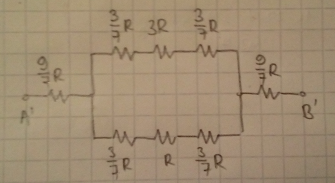 Which is very easy to solve:
R
e
q
=
7
9
R
+
(
7
3
R
+
3
R
+
7
3
R
)
+
(
7
3
R
+
R
+
7
3
R
)
(
7
3
R
+
3
R
+
7
3
R
)
×
(
7
3
R
+
R
+
7
3
R
)
+
7
9
R
=
7
1
8
R
+
7
2
7
R
+
7
1
3
R
7
2
7
R
×
7
1
3
R
=
7
×
4
0
(
1
3
×
2
7
+
1
8
×
4
0
)
R
=
3
.
8
2
5
Which is very easy to solve:
R
e
q
=
7
9
R
+
(
7
3
R
+
3
R
+
7
3
R
)
+
(
7
3
R
+
R
+
7
3
R
)
(
7
3
R
+
3
R
+
7
3
R
)
×
(
7
3
R
+
R
+
7
3
R
)
+
7
9
R
=
7
1
8
R
+
7
2
7
R
+
7
1
3
R
7
2
7
R
×
7
1
3
R
=
7
×
4
0
(
1
3
×
2
7
+
1
8
×
4
0
)
R
=
3
.
8
2
5
So, the solutions is 1 0 0 0 0 0 × 2 R e q = 1 9 1 2 5 0