Determine maximum value

By the Cauchy-Schwarz Inequality , $\left(\sum_{i=1}^n\sqrt{x_i}\right)\left(\sum_{i=1}^n\dfrac{1}{\sqrt{1+x_i}}\right)\le \left(\sum_{i=1}^n \left(\dfrac{x_i}{1+x_i}\right)^{1/4}\right)^2.$ It's not hard to show that $y=\left(\dfrac{x}{1+x}\right)^{1/4}$ is concave on $[0,\infty)$ . Hence, by Jensen's Inequality and using the hypothesis $\sum x_i=1$ we have $\sum_{i=1}^n \left(\dfrac{x_i}{1+x_i}\right)^{1/4}\le n\left(\dfrac{\frac{1}{n}\sum x_i}{1+\frac{1}{n}\sum x_i}\right)^{1/4}=\dfrac{n}{(n+1)^{1/4}}.$ Combining everything $\left(\sum_{i=1}^n\sqrt{x_i}\right)\left(\sum_{i=1}^n\dfrac{1}{\sqrt{1+x_i}}\right)\le \left(\sum_{i=1}^n \left(\dfrac{x_i}{1+x_i}\right)^{1/4}\right)^2\le \dfrac{n^2}{\sqrt{n+1}}.$ Equality occurs at $x_i=1/n$ for all $i$ . Our case is $n=24$ , giving an answer of $\frac{24^2}{\sqrt{25}} = 115.2.$

The NOOB way

change 24 to 1. Clearly, $x_1=1$ . So, the value is $\dfrac{1^2}{\sqrt{1+1}} .$

Change 24 to 2 ,assume $x_1=x_2=\dfrac{1}{2}. similary, the value is \dfrac{2^2}{\sqrt{2+1}} .$

So the answer is $\dfrac{24^2}{\sqrt{24+1}} .$ = 115.2

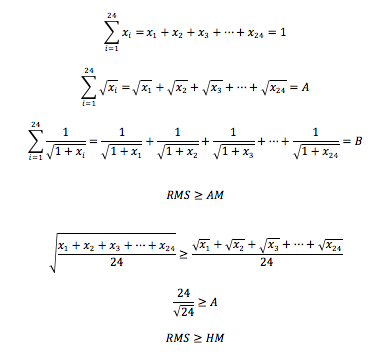
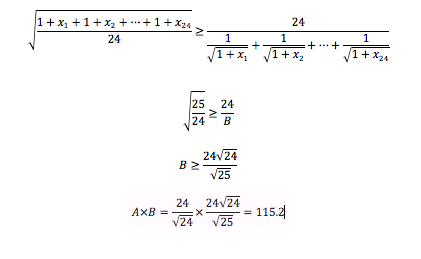
But i have my doubts in my solution, cause the first factor i got the max value, but in the second one i just got the value, so if someone please could offer a best answer would be much appreciated.

This one is bit lengthy by cauchy-swarchz (∑xᵢ)(1+1+1+1+1......)≥(∑(√(xᵢ))²(1 is added 24 times) ⇒1x24≥(∑(√(xᵢ))² ⇒√(24)≥(∑(√(xᵢ)).....(i) now we will find the min value of the other expression then miltiply the both (∑1/1+xᵢ)(1+1+1......)≥(∑(√(1+xᵢ))².....(ii) we have to use titu s lemma on (∑1/1+xᵢ) (1/x₁+1)+(1/x₂+1)..(1/x₂₄+1)≥((1+1+1+1....)²/(∑1+xᵢ)) ⇒(1/x₁+1)+(1/x₂+1)..(1/x₂₄+1)≥24²/25 put the value in equation (ii) (24²/25)×24≥(∑(√(1+xᵢ))² ⇒√(24³)/5≥∑(√(1+xᵢ)) multiply (i)and( ii) 24²/5≥∑(√(1+xᵢ)(∑(√(xᵢ)) ⇒576/5 =115.2