A JEE advanced problem

Probability Level 5

Probability of ten digit number formed by using $1,2,3,4~and~ 5$ so that the difference between any two consecutive digits is unity is equal to

Details and Assumptions

Surely u are allowed to repeat the digits.

Consider the difference of both $1,and~ -1$ between the numbers.

Do like and share

The answer is 0.00006635.

3 solutions

Tanishq Varshney
Mar 22, 2015

Its a bit long but I hope that u read it and tell any mistake if any freely.

Firstly total number of outcomes = For every place we have 5 choices of $1,2,3,4,5$ = $5^{10}$

Now coming on to number of favorable outcomes.

Let $a_{n+1},b_{n+1}~and ~c_{n+1}$ denote $(n+1)$ digit number whose $(n+1)th$ digit is $1~or~5$ , $2~or~4$ and $3$ respectively .

plz observe carefully.

$c_{n+1}=b_{n}$ [as with $3$ only $2$ or $4$ can come]

$a_{n+1}=b_{n}$ [as with $1$ only $2$ comes and with $5$ only $4$ comes]

$b_{n+1}=2 c_{n}+a_{n}$

[as $3$ can come with $2$ and $4$ but $1$ can come with only $2$ and $4$ can come with $5$ ]

$b_{n+1}=2 b_{n-1}+b_{n-1}$

$b_{n+1}=3 b_{n-1}$

we have to find $a_{10}+b_{10}+c_{10}$

= $b_{10}+2 b_{9}$ [from above relations]

$b_{9}=3 b_{7}$ and $b_{7}=3 b_{5}$ and $b_{5}=3 b_{3}$

thus $b_{9}=3^4 b_{1}$

as $b_{1}$ can be $2~or ~4$

$b_{9}=2\times 3^4$

similarly $b_{10}=3^4 \times b_{2}$

for $b_{2}$ there are $4$ choices

2 with 1 or with 3 and 4 with 5 or with 3.

$b_{10}=4\times 3^4$

thus favorable outcomes= $b_{10}+2 b_{9}=8\times 3^4$

$Probabaility =\frac{Number~ of~ favorable~ outcomes}{total~ number~of ~outcomes}$

most of u might be wondering how i took $c_{n+1}=b_{n}$ becoz

consider 2345432123 it is of type $c_{10}$ and leaving the 3 from right we get a number of type $b_{9}$

Tanishq Varshney - 6 years, 2 months ago

@Tanishq Varshney I got the answer afterwards. If we split the ten digits into five consecutive pairs, we can prove that:

The first pair can be chosen in $8$ ways.
Each subsequent pairs can be chosen in $3$ ways each. (This is not entirely true, since some pairs have more cases than others, but the total number is equivalent to multiplying by $3$ )

Hence answer is $(8*3^4)/5^{10}$

Note: Current answer is incorrect. Problem is waiting to be corrected.

Raghav Vaidyanathan - 6 years, 2 months ago

how was my solution, if any mistake do tell @Raghav Vaidyanathan

Tanishq Varshney - 6 years, 2 months ago

Shouldn't $c_{n+1} = 2 b_n$ , since 3 can come from 2 or 4?
Shouldn't $b_{n+1} = c_n + a_n$ , since 2 can come from 1 or 3?

This solution would be closer to what I think it would ultimately look like. Can you make the corresponding edit?

Calvin Lin Staff - 6 years, 2 months ago

sir if u could plz change the answer to 6.635E-5

Tanishq Varshney - 6 years, 2 months ago

Please make the edits throughout your solution first, to determine what the final answer should be.

For example, $a_{10} + b_{10} + c_{10} = b_9 + b_{10} + 2b_9 = b_{10} + 3 b_9$ .

After you are done, let me know what the answer should be.

Calvin Lin Staff - 6 years, 2 months ago

@Calvin Lin – I'm giving my solution here.

We will first divide the ten digits into five consecutive pairs. The first pair of numbers can be chosen in $8$ ways. The number of different pairs of form $Xa$ for $a \text{ in } (1,2,3,4,5)$ is given below. Also, the different ways of selecting the numbers for the next consecutive pairs has also been given:

$X1=1\quad \equiv (21)\rightarrow (21),(23)\\ X2=2\quad \equiv (12),(32)\rightarrow (12),(32),(34)\\ X3=2\quad \equiv (23),(43)\rightarrow (21),(23),(43),(45)\\ X4=2\quad \equiv (34),(54)\rightarrow (32),(34),(54)\\ X5=1\quad \equiv (45)\rightarrow (43),(45)$

Now, we have the different ways of selecting the first four numbers. Observe that the number of cases ending with each number has tripled. For example, for one pair, we had $2$ cases which ended in $3$ , but once we added another pair, we have $6$ cases which end in $3$ . Hence:

$\Rightarrow XYZ1=3,\quad XYZ2=6,\quad XYZ3=6,\quad XYZ4=6,\quad XYZ5=3$

We can easily see here that for every pair of numbers added, the number of cases which end in a certain digit is tripled. The first can be chosen in $8$ ways, adding subsequent pairs will multiply our number by a factor of $3$ . Hence, the number of favorable cases is $8*3^4$ .

@Calvin Lin

Raghav Vaidyanathan - 6 years, 2 months ago

@Raghav Vaidyanathan – would u plz correct ur latex code.

Tanishq Varshney - 6 years, 2 months ago

sir, in this 3212145432 if u take 4 with 3 then the consecutive difference wont be unity.

Tanishq Varshney - 6 years, 2 months ago

i guess my answer 6.635E-5 is correct sir, so kindly plz change the answer

Tanishq Varshney - 6 years, 2 months ago

Thanks. I have updated the answer accordingly.

Calvin Lin Staff - 6 years, 2 months ago

What's wrong with this logic? (for the number of favourable cases) @Calvin Lin

Choose the first digit in 5 ways. For every choice of $kth$ digit, there exist 2 choices for $(k+1)th$ digit. So, number of favorable cases is $5\times 2^9$ .

Deeparaj Bhat - 5 years, 1 month ago

If the first number is 1, how many choices are there for the 2nd number?

Calvin Lin Staff - 5 years, 1 month ago

Thanks for pointing out my mistake.

Deeparaj Bhat - 5 years, 1 month ago

Did exactly the same! Nice problem! We can find the general answer -

$\displaystyle \text{Number of such n-digit numbers using any 5 consecutive digits} = \begin{cases} 5, \text{if} \ n =1 ; \\ 14 \times 3^{(n-1)/2}, \text{if n is odd} \\ 8 \times 3^{n/2 -1}, \text{if n is even} \end{cases}$

Kartik Sharma - 4 years, 5 months ago

Adit Mohan
Apr 14, 2015

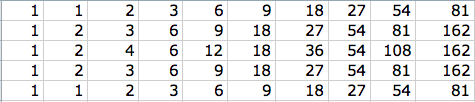
I've used a path counting approach. the rows represent each digit 1 through 5 and the columns represent the positions 1 through 10.
The number in each box represent he number of ways it is possible to have the corresponding digit at the corresponding position.
the numbers in the first column will all be one and the subsequent numbers can be obtained by adding the numbers in the top and bottom left boxes. hence total ways = 81+162+162+162+81=648.
probability = no of favorable ways/total possibilities=648/5^10=6.635E-5.

Joe Mansley
Jun 4, 2021

Let's count the number of allowed numbers.

Every other digit must be even.

Let $a_n$ denote the number of 2n-digit allowable numbers, starting with a 2. The next digits can be either $12$ , $32$ or $34$ .

So $a_n=3a_{n-1}$ .

$a_1=2$

So $a_5=2 \cdot 3^4$

Half of the allowable numbers will start with an even, and half of those will start with a 2. So the number of allowable numbers is $8 \cdot 3^4=648$ .

So the probability is $648/5^{10}$ .

A JEE advanced problem

The answer is 0.00006635.

3 solutions

0 pending reports