A Deflected Charge
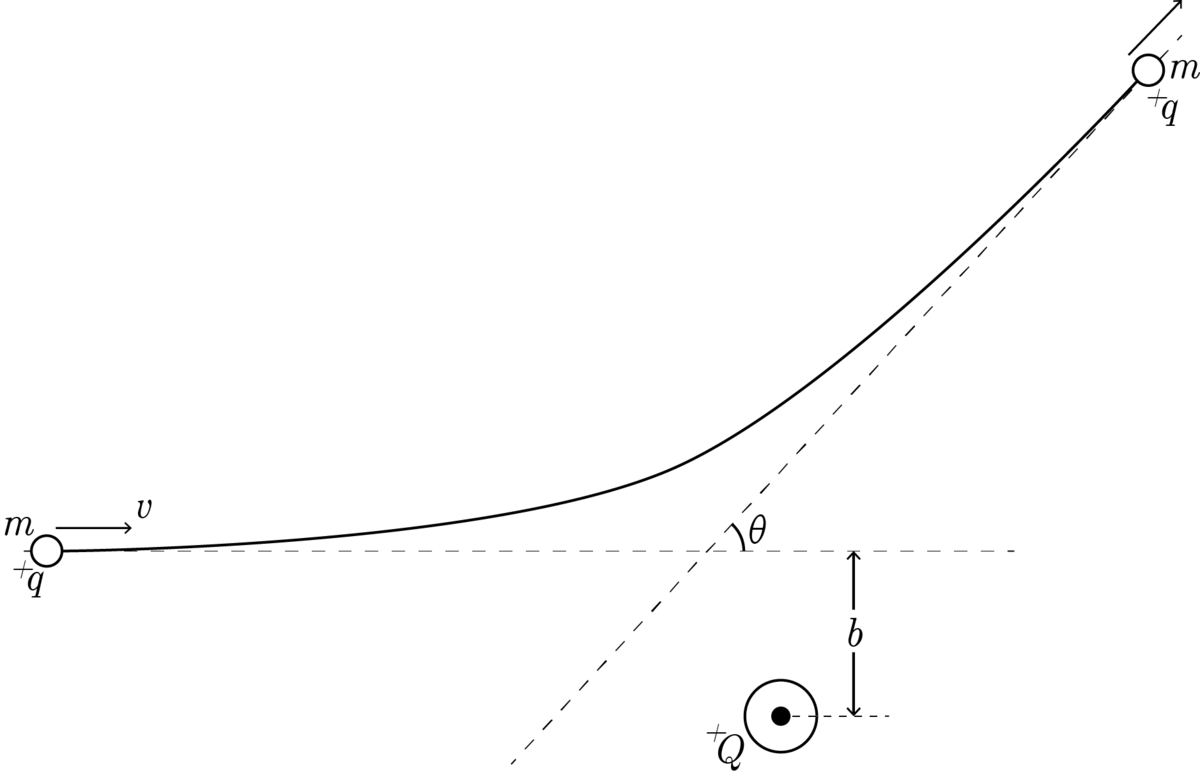
A charged particle of charge + q and mass m is moving from infinity towards a charge + Q with a velocity v . The particle is eventually deflected due to the repulsion force in accordance with Coulomb's law.
Given the impact parameter b , find the scattering angle, θ , in degrees.
Details and Assumptions
- Assume that this system is in isolated gravity free space.
- The charge + Q is fixed.
- Only Coulombic forces are present.
- Impact parameter is the distance between the line of incidence and the fixed charge.
- Scattering angle is the angle made by terminal velocity with initial velocity.
- Take q = 1 . 0 e , Q = 6 . 0 e , m = 1 . 6 7 × 1 0 − 2 6 kg , v = 1 0 8 9 ms − 1 , b = 5 7 nm .
- e is elementary positive charge.
The answer is 101.4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice solution! but how do you get such brilliant ideas in physics?
Log in to reply
As in forming question?
Log in to reply
I believe this is the easier way to solve this problem. But the only thing I don't get is how you got the two infront of the arctan.
(use http://s1.daumcdn.net/editor/fp/service nc/pencil/Pencil chromestore.html for LATEX converter by copying and pasting LATEX into bottom. )
First since you know that the momentum is a great way to take the electrostatic force into account. This is because
F= dp/dt and if you integrate both sides by dt you get momentum.
\int { F } dt\quad =\quad p
Now if we look back we see that we have a constant force and that F now goes outside the integral. So now it looks like this
F\cdot \Delta t\quad =\quad \Delta p
now the force is by Columbs law (since it is a point charge) or intrinsically Gauss's Law.
\frac { Qq }{ 4\pi { \Ep }_{ 0 }{ b }^{ 2 } }
remeber that the velocity is v and b is the distance so
\frac { Qq }{ 4\pi { \Ep } { 0 }{ b }^{ 2 } } \cdot \frac { b }{ v } =\quad \frac { Qq }{ 4\pi { \Ep } { 0 }{ b }v } =\quad F\cdot \Delta t\quad
now we see a right triangle with the change in momentum being upward. We just divide by (mv) to get the tangent of the angle and for the final answer the inverse tan of the value.
\frac { Qq }{ 4\pi { \Ep } { 0 }{ b }v } \div \frac { mv }{ 1 } =\quad \frac { Qq }{ m4\pi { \Ep } { 0 }{ b }{ v }^{ 2 } } =\quad \tan { (\theta ) }
now
{ tan }^{ -1 }\left( \frac { Qq }{ m4\pi { \Ep }_{ 0 }{ b }{ v }^{ 2 } } \right) =\quad { \tan { (\theta ) } }^{ -1 }=\theta \quad =\quad 50.7
I believe this is the correct answer as the angle phi you added is worthless as the interaction does not have anything to do with it. If you do not think this is the right way Can you explain why not and what steps I missed. (Think about the fact that the diagram is not drawn to scale). Thanks
Log in to reply
@Austin Joseph – Can you just use \[ a n d \) between these latex because Daum does not work for me. Thanks!
Log in to reply
@Kishore S. Shenoy – I'm sorry I don't understand what you mean by the or\and thing but I looked at the problem again and realized that I just estimated it instead of integrating it which left out a factor of 2.
Log in to reply
@Austin Joseph – Problem solved? Sorry, I couldn't read the LaTeX code. Daum did not work either... :(
See this :-
Log in to reply
@Kishore S. Shenoy – Hey Kishore are you doing IPHO
Log in to reply
@Austin Joseph – I don't think I'll get selected for NSEP because I've learnt only till Gravitation...Only Dynamics
Log in to reply
@Kishore S. Shenoy – So you don't know Maxwell's Laws?
Log in to reply
@Austin Joseph – Nope, not at all deep... I just remember learning a non vector equation last year...
Log in to reply
@Kishore S. Shenoy – what do you use for calculus since it seems like my problem with your problems is that I am not well developed in calculus
Log in to reply
@Austin Joseph – I am 8th Standard what about you?
@Austin Joseph – Well, you saw the mistake that popped with your first solution, in which you estimated... That is where you need calculus... For estimating or summing small change though out so that you'll get a number that's not very small... For example, when acceleration is not constant in a motion, we take a small infinitesimal small time gap d t in which you can consider acceleration to be constant... Working on to reach where you want and then integrate to get the required answer. In general, for summing up small infinitesimal value, we use integration, and converting known equation to the infinitesimal for, we use differentiation. Ask for more description... I'm in 11 t h grade and I think calculus is well above your grade, though you can start learning it... You require only the basics right now. Only that how to use it will be tricky at first. All the best!
Log in to reply
@Kishore S. Shenoy – I know basic differentiation, integration, and Integration by parts but learned it all from learning limits and then deriving the derivatives for myself. But I need a proper book. Any suggestions?
Log in to reply
@Austin Joseph – For pure calculus or calculus for physics?
Log in to reply
@Kishore S. Shenoy – If you know good books on each it would be helpful. Thanks
Log in to reply
@Austin Joseph – Well you could take "A First Course in Calculus" by Serge Lang for basic calculus and "Problems in General Physics" by Igor Irodov for Applications of calculus.
Log in to reply
@Kishore S. Shenoy – Thx. I have Irdov and thx for the other book. This should help
Yes !! in question forming
Log in to reply
@Pankaj Gupta – I got inspired by Rutherford's α -ray scattering experiment...
I think these ideas in the solution will help in solving I don't expect anybody to solve this - Part (2) , won't it?
Log in to reply
Isn't this solution the same one as given in Arthur Beisers discussion on α scattering......Nicely presented.....But the approach needed some ingenuity. I solved by using hyperbolic orbits.....
I solved using simple approach based on energy conservation and hyperbolic path........But the way you used Maths over here....That's awesome.....
Log in to reply
Can you show your method?
Log in to reply
Similar to the 3rd solution posted here.I just worked with Cartesian coordinates though.
Hyperbolic orbits can really really simplify the problem!! I did it the same way :)
Just solve the equation of motion to find the trajectory of the particle. The equation of motion of the scattered particle is m r ¨ = 4 π ϵ 0 r 2 q Q r ^ where r is the position vector of the particle, and r ^ is a unit vector in the direction of r . Then r × r ¨ = 0 , and so h = r × r ˙ must be constant. Introduce a fixed right-handed orthonormal triad of unit vectors i , j , k so that h = h k where h > 0 and where i points along the direction from which the incident particle is coming. Since r ⋅ h = 0 , we deduce that the particle moves entirely in the plane defined by the vectors i , j , so we can define planar polar coordinates r , θ such that r ^ = r cos θ i + r sin θ j . Standard calculus shows us that r 2 θ ˙ = h and that the differential equation becomes m ( r ¨ − h 2 r − 3 ) = 4 π ε 0 m q Q r − 2 = k r − 2 If we define u = r − 1 , then r ˙ = − h d θ d u r ¨ = − h 2 u 2 d θ 2 d 2 u and so the equation becomes d θ 2 d 2 u + u = − h 2 m k which has the general solution u = A cos θ + B sin θ − h 2 m k . Since the particle is at infinity with incoming speed v with impact parameter b at time t = 0 , we see that h = v b and moreover that u = 0 and d θ d u = b − 1 when θ = 0 . Thus u = h 2 m k cos θ + b 1 sin θ − h 2 m k . If we put R = h 4 m 2 k 2 + b 2 1 α = tan − 1 k b h 2 m = tan − 1 k v 2 b m = tan − 1 ( q Q 4 π ϵ 0 m b v 2 ) then we have u = R [ cos ( θ − α ) − cos ( α ) ] and hence u = 0 when θ − α = ± α , and so when θ = 0 , 2 α .
Thus the scattering angle is π − 2 α radians, which evaluates to 1 0 1 . 4 ∘ for the given constants of this problem.
Using the Energy , Angular momentum conservation we get r m
so L = m v 0 b
hence E = 2 1 m v 0 2 + r 0 k e Q
2 1 m v 2 + r m k e Q = 2 1 m v 0 2 + r 0 k e Q
r 0 → ∞ so
2 1 m v 2 + r m k e Q = 2 1 m v 0 2
2 1 m v 2 + r m k e Q − 2 1 m v 0 2 = 0
using Angular momentum conservation we yield that
L = m v r m s i n ( π / 2 ) = m v r m → m v r m = m v 0 b → v = v 0 b / r m
so
2 1 m ( v 0 r m b ) 2 + r m k e Q − 2 1 m v 0 2 = 0
so we multiply bothsides with r + m 2 so
2 1 m ( v 0 b ) 2 + k e Q r m − 2 1 m v 0 2 r m 2 = 0
so r m = m v 0 2 − b − ( k e Q ) 2 − 4 2 1 m v 0 2 ∗ 2 1 m ( v 0 b ) 2
Now the path represent an hyperbola , a = r m − c o s θ / 2 b , c = c o s θ / 2 b
we know that we can express a hyperbola in polarcoordinates with
r = 1 − ϵ c o s θ r m when r gets to infinity 1 − ϵ c o s θ = 0
1 = ϵ c o s θ
1 = a c c o s θ
solving the Trigonometric equation we yield
θ = 1 . 7 7 r a d
Let
So, we can say p 2 = 2 m T
Due to symmetry, ∣ p i ∣ = ∣ p f ∣ = p (Say)
Since, the path is symmetric, we need only take component of force along the change in momentum to get its magnitude.
F r = r 2 k q Q ∣ Δ p ∣ = ∫ − ∞ ∞ F cos ψ d t = ∫ − ∞ ∞ r 2 k q Q cos ψ d t
Conserving angular momentum, p b = m r 2 ω = m r 2 ψ ˙ So, d t = ψ ˙ d ψ = p b m r 2 d ψ
From basic geometry, 2 φ + θ = π φ = 2 π − 2 θ
Hence, ∣ Δ p ∣ = ∫ − ∞ ∞ r 2 k q Q cos ψ d t = ∫ − φ φ r 2 k q Q cos ψ p b m r 2 d ψ = ∫ − φ φ p b k q Q m cos ψ d ψ = p b 2 k q Q m sin φ = p b 2 k q Q m cos 2 θ
Using sine rule, sin φ ∣ p i ∣ = sin θ ∣ Δ p ∣ ⇒ ∣ Δ p ∣ = 2 p sin 2 θ
⇒ 2 p sin 2 θ = p b 2 k q Q m cos 2 θ ⇒ tan 2 θ = p 2 b k q Q m = 2 T b k q Q = 2 b D = m v 2 b k q Q
∴ θ = 2 tan − 1 ( 2 b D ) = 2 tan − 1 ( 4 π ε 0 m v 2 b q Q )