A Little Prime For Your Mind

If $n \leq 1$ then $n^5 - 1 \leq 0$ , so we may assume $n \geq 2.$

Then $n^5 - 1 = (n-1)(n^4 + n^3 + n^2 + n + 1)$ and $1 \leq n-1 < n^4 + n^3 + n^2 + n + 1$

If $n-1 > 1$ then this shows $n^5 - 1$ is the product of two integers larger than $1,$ and therefore it couldn't be a prime.

The only remaining case is $n=2$ which yields the example $31$ given in the problem statement. We can therefore conclude that $\boxed{\text{no}}$ other primes can be written as $n^5-1$ for an integer $n$ .

Other than the first prime 2, the larger primes are odd. Therefore, for $n^5 - 1$ to be a prime, $n$ must be even and we can write $n=2m$ , where $m$ is a positive integer. Then we have:

$n^5-1 = (n-1)(n^4+n^3+n^2+n+1) = (2m-1)(n^4+n^3+n^2+n+1)$

We note that other than $m=1$ , then $n=2$ and $2m-1 = 1$ , $n^5-1 = {\color{#D61F06}\underbrace{(2m-1)}_{\ne 1}}(n^4+n^3+n^2+n+1)$ is always a composite.

(Edit: this solution came to my mind at a time but has a wrong assumption and it's not correct. Please see the Moderator note on it)

The result of multiplying odd numbers together is always an odd number and odd number -1 is an even number and 2 is the only even prime number exists.

Since n^5 -1 is a prime number n > 0. Note that n^5 - 1 can be factorized as (n-1)(1+n+n^2+n^3+n^4) which is clearly a product of 2 natural numbers. A prime no. is only divisible by itself and one. Thus (n-1) = 1 and so n=2 is the only solution for which n^5 -1 is prime.

Since $n \equiv 1 (\textrm{mod}\ n - 1)$ for all integer $n > 2$ , it follows that $n^5 \equiv 1 (\textrm{mod}\ n - 1)$ by raising both sides to the 5th power, and thus that $n^5 - 1 \equiv 0 (\textrm{mod}\ n - 1)$ .

So $n - 1$ factors $n^5 - 1$ , meaning that if $n > 2$ , $n^5 - 1$ cannot possibly be prime.

Of course, if $n < 2$ then $n^5 - 1 \le 0$ , but all primes are positive, so we can rule that out too.

Therefore, if $n \ne 2$ , $n^5 - 1$ is not prime.

In fact, we can use similar logic to show a more general result: if $a ^ p - 1$ is prime for natural numbers $a, p$ , then $a = 2$ or $p = 1$ . This is proven on the Wikipedia page for Mersenne primes .

This one's quite easy; since $n^5 - 1 = \left( n-1 \right) \left( n^4 + n^3 + n^2 + n + 1 \right)$ , we must deduce that, for any $n > 2$ , $n^5 - 1$ must be the product of at least two integers greater than $1$ .

Simply, because

(n^5-1)=(n-1)(n^4+n^3+n^2+n+1),

there can't be another prime except for n=2. Thus,

Answer= No

For n greater than 2, n-1, which is a factor of n to the power of 5 -1, is greater than 1. So n to the power of 5-1 is composit.

$n^5-1=(n-1)(n^4+n^3+n^2+n+1)$ . When n > 2, there will always be at least 2 factors, which makes $n^5-1$ a composite number.

I used modular arithmetics to solve this:

We assume that a prime number has to be a positive integer. If n ≤ 1, then n^5 - 1 is too small to be a prime. So let n be an integer greater than 2.

Then (n mod n-1) = (1 mod n-1), and (n * n * n * n * n mod n-1) is also equal to (1 mod n-1). Therefore, (n^5 - 1 mod n-1) = (0 mod n-1), i.e. n^5-1 is divisible by n-1 and therefore not a prime (since n-1 < n^5 -1)

n^5 - 1 can always be written in base n as the numeral “#{n-1}” repeated five times. (I say “numeral” because no matter how large the base, you would have to find a single symbol, such as a letter, to represent n - 1.) But that means that for any n you pick, the total value will be divisible by n - 1, and also by “11111” base n. The only reason that 2^5 - 1 happens to be prime is that 2 - 1 = 1, and “11111” base 2 = 31, and a prime number is allowed to be divisible by 1 and also itself. For any other n, the equation yields a composite number.

n^5-1 = n (n^4 -1) + (n-1) = n(n^2 -1)(n^2 +1) + (n-1) = n (n-1)(n+1)(n^2 +1) + (n-1)

This is divisible by 1, n^5-1 and n-1. For n>2, no. of factors > 2

$a^n - b^n$ is always divisible by $a - b$ , because

$a^n-b^n=(a-b)\Big(\sum_{i=0}^{n-1}a^{n-1-i}b^i\Big)$

Assume that there does exist a prime $p > 31$ which can be expressed in the form $n^5 - 1$

In this case, we have: $n^5 - 1^5 \implies n-1 \vert n^5 - 1$

But this is a contradiction, since $p$ has no divisors except 1 and itself. So there is no other prime that can be expressed in this form.

The first thing I did was to look for a pattern:

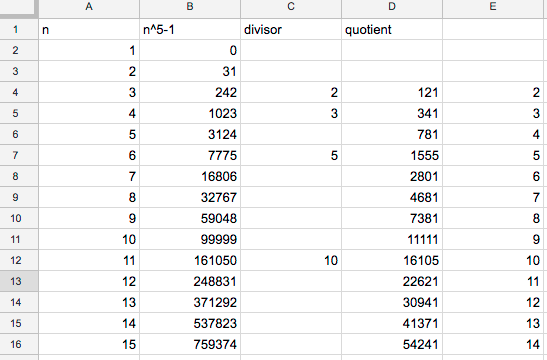
I noticed that each term was divisible by $n-1$

From here all you have to do is show that $n-1$ is always a factor of $n^5-1$

The Factor Theorem says that since there is a value for $n$ that satisfies both $n-1=0$ and $n^5-1=0$ then $n-1$ is a factor of $n^5-1$

Multiplying odd numbers together must gives us odd numbers, and an odd number -1 is an even number. In order to get prime number, n must be even.

Notice that for n=4 , $n^{5}-1=1023$ .1023 has a factor 3. And for n=6, $n^{6}-1=7775$ . 7775 has a factor 5. So assuming that for n=2t, we have factor 2t-1.

Here is the proof:

$\begin{aligned} n^{5}-1&=32t^{5}-1\\ &=32t^{5}-2t+2t-1\\ &=2t\left( 16t^{4}-1\right) +2t-1\\ &=2t\left( 4t^{2}+1\right) \left( 4t^{2}-1\right) +2t-1\\ &=\left( 2t-1\right) \left[ 2t\left( 4t^{2}+1\right) \left( 2t+1\right) +1\right] \end{aligned}$

In conclusion, except for n=2 , we can't get a prime number

All other results are products of primes by definition.