A Little R&R (repel and relaxation)

Electricity and Magnetism Level 3

$N$ particles with electric charge $q$ are placed on a unit sphere at random. They repel each other and relax toward an equilibrium configuration as their motion damps away.

In the code box below, design an algorithm that computes the potential energy of the equilibrium.

Details & Code:

Enter your answer for $N=17$ in units where $\frac{q^2}{4\pi\epsilon_0}=1.$
The function U(listofPoints) takes a list of NumPy arrays containing the position vectors of each of the $N$ charges, and returns the total potential energy $\sum\limits_{i=1}^N \sum\limits_{j \gt i}^N \frac{1}{r_{ij}}.$

def U(listofPoints):

    N = len(listofPoints) #number of charges in list
    U = 0

    #Loops through unique pairs of charges
    for i in range(N):
        for j in range(i + 1, N):
            r = listofPoints[i] - listofPoints[j]
            U = U + 1.0 / numpy.linalg.norm(r)
    return U

import numpy

Python 3

The answer is 106.050405.

4 solutions

Hosam Hajjir
Nov 15, 2017

Here is how the charges look like after reaching equilibrium. They are plotted against a spherical wire frame that has a separation of $30^{\circ}$ for both $\theta$ and $\phi$ .

Steven Chase
Nov 6, 2017

I used a hill-climbing algorithm to solve. I'm sure the code provided is perfectly fine, but I understand best if I write it myself from scratch. The minimum potential ends up being about 106.05

import math
import random

################################################

N = 17

R = 1.0

delta = 10.0**(-3.0)

################################################

# Angular parameters

theta = []
phi = []

################################################

# Mutated angular parameters

theta_m = []
phi_m = []

################################################


# Initialize theta and phi arrays

for j in range(0,N):
    theta.append(2.0 * math.pi * random.random())
    phi.append(-math.pi/2.0 + math.pi * random.random())

################################################

# Initialize mutated theta and phi arrays

for j in range(0,N):
    theta_m.append(0.0)
    phi_m.append(0.0)

################################################

#print len(theta)
#print len(phi)

################################################


# Minimum potential energy seen over trials

Umin = 99999999999.0

################################################


# Run a hill-climbing algorithm to converge on the minimum-U configuration

for j in range(0,10**5):

    # Mutate the angular parameters

    for k in range(0,N):
        theta_m[k] = theta[k] + delta * (-1.0 + 2.0 * random.random())
        phi_m[k] = phi[k] + delta * (-1.0 + 2.0 * random.random())

    # Calculate the potential

    U = 0.0

    for k in range(0,N):         # Every new charge added
        for n in range(0,k):    # Interacts with every other charge already there
            if k != n:          # Except for itself

                x1 = R * math.cos(theta_m[k]) * math.cos(phi_m[k])
                y1 = R * math.sin(theta_m[k]) * math.cos(phi_m[k])
                z1 = R * math.sin(phi_m[k])

                x2 = R * math.cos(theta_m[n]) * math.cos(phi_m[n])
                y2 = R * math.sin(theta_m[n]) * math.cos(phi_m[n])
                z2 = R * math.sin(phi_m[n])

                delx = x1 - x2
                dely = y1 - y2
                delz = z1 - z2

                d = math.sqrt(delx**2.0 + dely**2.0 + delz**2.0)

                U = U + 1.0/d

    # If new best solution is found, store as such

    if U < Umin:
        Umin = U

        for k in range(0,N):
            theta[k] = theta_m[k]
            phi[k] = phi_m[k]


################################################

print Umin

How did you get the time for all that?

Annie Li - 3 years, 7 months ago

I think it took me about an hour

Steven Chase - 3 years, 7 months ago

Wow. That is quite a long time!

Annie Li - 3 years, 7 months ago

Laszlo Mihaly
Nov 15, 2017

I am not sure if this link will work for you all, but here is an article discussing this problem, T Erber and G M Hockney 1991, J. Phys. A: Math. Gen. 24 L1369

They went up to N=65. They pointed out that metastable configurations start to appear above N=16. (N=17 has no metastable solution.)

Mark Hennings
Nov 13, 2017

This is just the $N=17$ solution to the Thomson problem , and the answer is $\boxed{106.050404829}$ .

Thanks for the info. Interesting to see that this doesn't appear to be a trivial problem, from the perspective of formal mathematics.

Steven Chase - 3 years, 7 months ago

Mathematically it's not easy, but electrons on a conducting sphere somehow get it right every time. Algorithms to generate the equilibrium configurations are tough to come by too, so we thought we'd open up the problem to the Brilliant community.

Aaron Miller Staff - 3 years, 7 months ago

Another fun one is finding the equilibrium position for 20 (or so) masses chained together with springs to form a sort of discrete catenary.

Steven Chase - 3 years, 7 months ago

@Steven Chase – I tried (and failed) to solve the discrete catenary problem last night. Is there a closed-form solution, or do you have to solve it numerically?

Aaron Miller Staff - 3 years, 6 months ago

@Aaron Miller – Thanks for your interest

I know of two ways to do it:
1) Use a search algorithm (hill-climbing, etc.)
2) Do a small-time-step physics simulation with some viscosity in the environment (so it doesn't oscillate forever)

I've actually posted a small version of it. Might be fun to do a bigger version too.

https://brilliant.org/problems/how-hard-could-two-springs-be/?ref_id=1399743

Steven Chase - 3 years, 6 months ago

@Aaron Miller – Suppose that $2K-1$ point masses, each of mass $m$ , are joined by $2K$ light inextensible rods each of length $1$ . The linkages at the masses are smooth. This model of a chain is suspended between two points $A,B$ at the same vertical height and a distance $2L$ apart, where $0 < L < K$ .

The system is symmetric, and the middle mass will be supported by two rods, each at angle $\theta_1$ to the horizontal, each under tension $T_1$ . These two rods are in turn attached to rods making angles $\theta_2$ to the horizontal, each under tension $T_2$ . And so on up, until the last two rods (which fix the chain to the points $A,B$ ) are under tension $T_K$ and make an angle $\theta_K$ with the horizontal.

Since there is no horizontal motion, we have $T_k\cos\theta_k = T_{k-1}\cos\theta_{k-1}$ for all $k$ . The $k$ th pair of rods are supporting $2k-1$ point masses, and hence $2T_k\sin\theta_k = (2k-1)mg$ If we write $2T_k\cos\theta_k = mg\gamma^{-1}$ for all $k$ , we deduce that $\tan\theta_k = (2k-1)\gamma$ for all $k$ . In addition, we require that $L \; = \; \sum_{k=1}^K \cos\theta_k \;= \; \sum_{k=1}^K \frac{1}{\sqrt{1 + \gamma^2(2k-1)^2}}$ which enables us to determine the value of $\gamma$ , at least numerically.

The case $L=5$ , $K=10$ is shown below, and the positions of the point masses are compared with the catenary for a continuous chain of length $2K$ hanging between the points $A$ and $B$ .

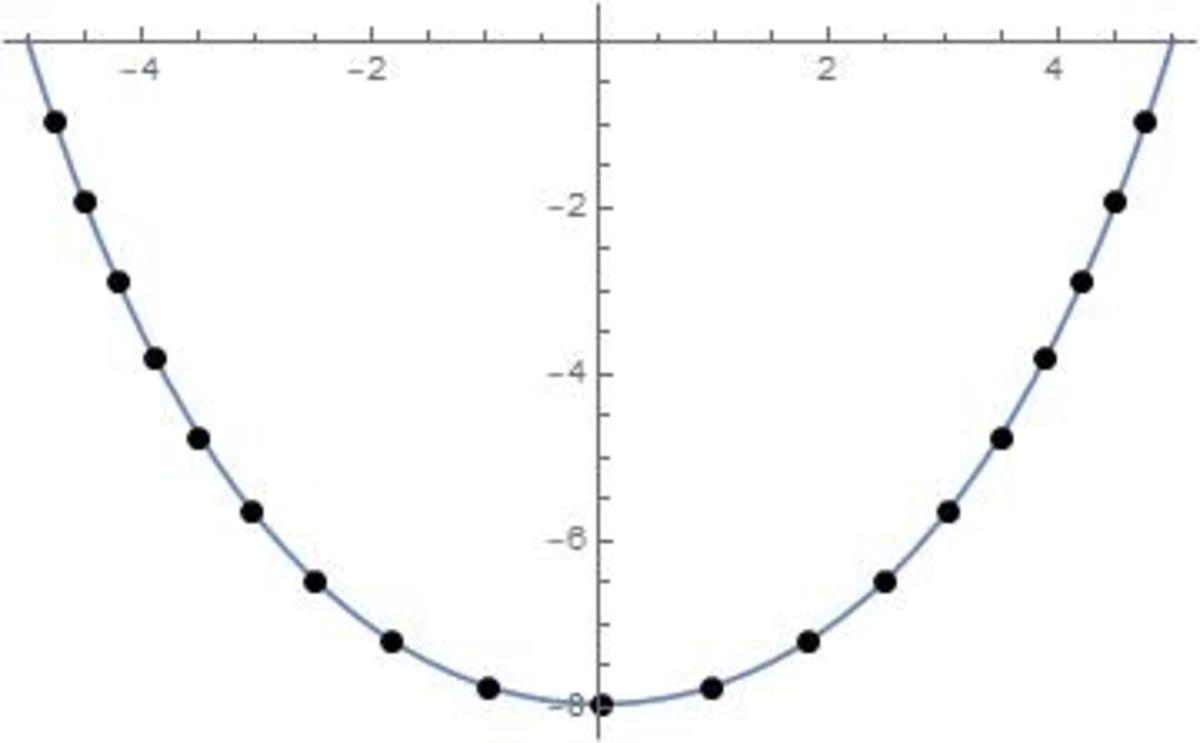
A similar model can be used to consider the alternative view where the chain is comprised of uniform bars of length $1$ and mass $m$ linked smoothly together...

If the connecting rods were light springs, then we would still have similar equations for the angles $\theta_k$ , but now the values for the tensions $T_k$ would tell us the lengths of the springs (given the spring constant). We would still have the requirement of the horizontal spread from $A$ to $B$ being $2L$ to give us a condition to determine the constant $\gamma$ ...

Mark Hennings - 3 years, 6 months ago

@Mark Hennings – Thanks, @Mark Hennings . Nice answer! I should have tried it with rigid rods first, but I jumped straight to springs and found myself in an algebraic quagmire, even for two springs. Look for some catenary problems in the coming weeks. I hope you'll reshare your clear insights.

Aaron Miller Staff - 3 years, 6 months ago

A Little R&R (repel and relaxation)

The answer is 106.050405.

4 solutions

0 pending reports