A long slipway!
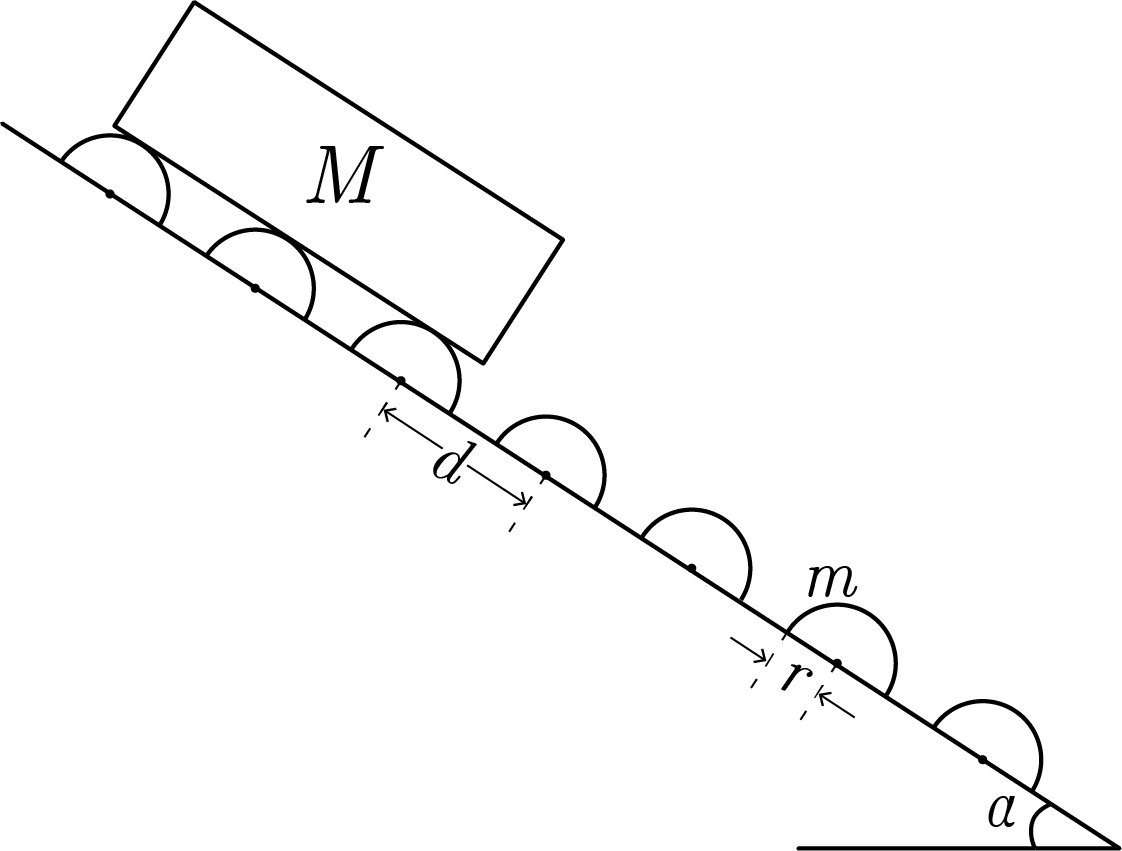 There is long slipway, inclined at an angle
α
with the ground, has many identical rollers, fitted at a a distance
d
between them. The rollers have horizontal axles and consist of rubber-covered solid steel cylinders each of mass
m
and radius
r
. A plank of mass M, is released at the top of the slipway.
There is long slipway, inclined at an angle
α
with the ground, has many identical rollers, fitted at a a distance
d
between them. The rollers have horizontal axles and consist of rubber-covered solid steel cylinders each of mass
m
and radius
r
. A plank of mass M, is released at the top of the slipway.
Find terminal velocity v m a x of the plank. Submit your answer to 3 decimal digits.
Details and Assumptions
- The rollers are covered with rubber so that there is friction between the plank and the block
- The rollers start pure rolling (no slipping) just as they lose contact with the plank.
- Initially, there is slipping between the plank and the rollers
- Take the length of the plank to be much greater than d , i.e. d ≪ L
- Take M = 1 0 k g , m = 5 0 0 g , d = 1 0 c m , r = 3 c m , α = 3 π .
The answer is 5.886.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
How did you get 2 1 I ω m a x 2 + d L Q = d L I ω m a x 2 ?
Shouldn't it be 2 1 I ω m a x 2 + d L Q = d L Q = 2 d L I ω m a x 2
Log in to reply
What I typed was wrong and what you say seems to be incorrect. Please check the corrected solution.
Log in to reply
Got it. Thanks.
I thought you were approximating since d L Q > > 2 1 I ω m a x 2
Log in to reply
@Siddhartha Srivastava – Your welcome! Actually both are equal... ☺
Dear Author, it seems to me, that in the last formula you used a wrong value of the angle and hence its sin. Didn't you?
Log in to reply
Seems so... I think it should be α = 6 π . Right?
Log in to reply
correct answer 5.826
Log in to reply
@Aryan Goyat – It's 5 . 8 8 5 6 6 . . . right?
It also seems that you have not put the correct dimensions for various physical quantities.and my answer was the same that you posted of . The correct answer is 5.88. Please check up.
this is the 3rd time it's posted by some one on brillant!
When the block covers a distance L , it rotates d L rollers to an angular velocity ω m a x = r v m a x
Now let us take that f ( t ) be the kinetic friction acting between the roller and the block. We cannot say whether it has a time dependency or not so that we take it to be dependent. And let's take that it acts for a d t time.
So,
r × f ( t ) d t OR r × f ( t ) Δ t ⇒ r ∫ f ( t ) d t And f ( t ) = I d ω = I Δ ω = I ω m a x = r I d t d ω
Now let us take the loss in energy when the block slips on one of the rollers, since there is kinetic friction. So, loss in Energy is the difference in work done by friction in the block and the roller.
⇒ d Q ⇒ Q ∴ Q = f ( t ) [ v m a x − r ω ] d t = r ω m a x ∫ f ( t ) d t − r ∫ f ( t ) ω d t = r ω m a x ∫ f ( t ) d t − r ∫ r I ω d ω = I ω m a x 2 − I 2 ω m a x 2 = 2 1 I ω m a x 2
So heat lost when it covers L distance = d L Q
Now we can conserve energy,
M g L sin α ⇒ v m a x = d L ( 2 1 I ω m a x 2 + Q ) = d L I ω m a x 2 = d L 2 m v m a x 2 = m 2 d M g sin α [ ∵ I = 2 1 m r 2 and ω m a x = r v m a x ] ∴ v m a x = m 2 d M g sin α
Substituting, v m a x = 1 0 × 2 2 × 1 0 × 1 0 × 2 × 3 = 2 5 3 ≈ 5 . 8 8 5 6 6 . . .
This solution is not original. It is put to share amazing insight of the problem maker.