A magic 8?

If each row adds up to $n$ , then all $9$ squares add up to $3n$ .

Also, if we add up the four lines that pass through $8$ , we get the sum of all squares $+ 3$ additional $8$ 's, or $3n + 3 \cdot 8$ . But this also adds up to $4n$ , since it is four groups of three that add up to $n$ each.

Therefore $3n + 3 \cdot 8 = 4n$ , or $n = \boxed{24}$

Here is one way to do it:

A square in which every column, row, and diagonal add up to the same number is called a magic square . A well-known $3 \times 3$ magic square is as follows, where the middle number is $5$ and every column, row, and diagonal add up to $15$ :

Adding $3$ to every number in the above magic square would change the middle number to $8$ , but now every column, row, and diagonal would add up to $15 + 3 \cdot 3 = \boxed{24}$ .

When using consecutive integers to bulid the given table $n = 3 \times m$ where $m$ is the middle number.

In this case $m = 8\ \ \text{then}\ n = 3 \times 8 = 24$

Here is my brute force method of doing it using python and the Itertools package. Not the most intelegent way to do it... but it is fun programming :D

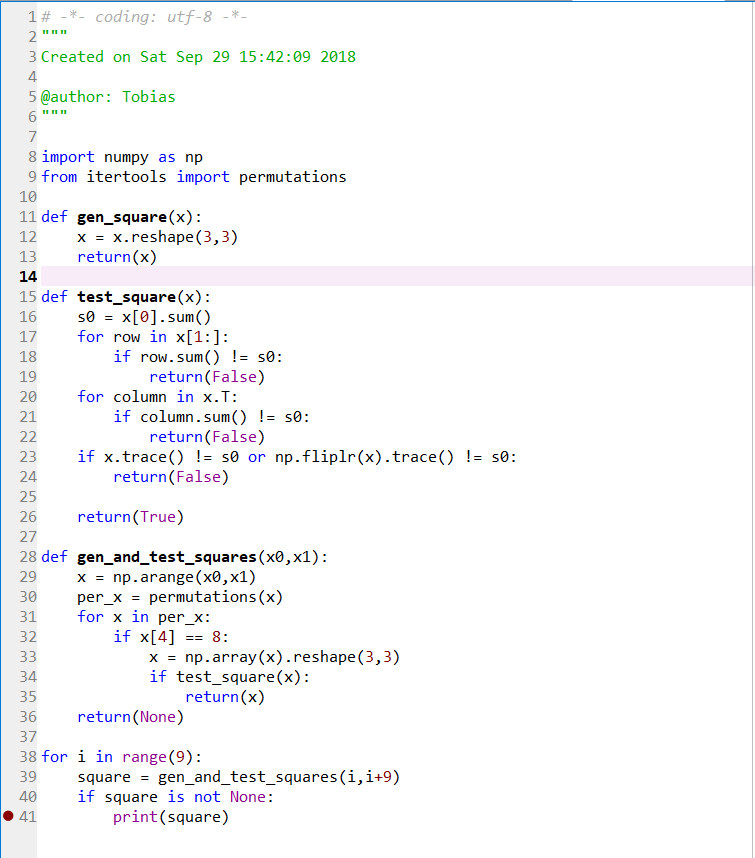
Prints out: [[ 5 10 9] [12 8 4] [ 7 6 11]]

Consider any magic square with a center of value x. To get every value to be the same, you need to balance the values surrounding it. A good way to go about this is with modular math, which is this in the case of consecutive numbers.

As you can see, the amounts over and under x manage to cancel out in each row, square, and column. You wind up with each row, square and column being 3x. In this case, 24.

The well known solution for 1 to 9 consecutive digits is 15 and it has 5 at the center instead of 8. Therefore adding 3 to each digits gives us consecutive digits from 4 to 12 with 8 at the center and

Answer=15+3*3=24

Nine consecutive numbers containing 8 can be anything from 1 to 9 to 8 to 16. Since 8 is the middle number of the grid, all the other numbers must include the 8 in a sum of three numbers that has the same total. To make this feasible, the largest number, plus 8, plus the smallest number must give the same sum as the second largest number, plus 8, plus the second smallest number, and so on. From this it follows that 8 must be the middle value number of the sequence, so the sequence must be 4 to 12. Hence 4 + 8 + 12 = 24

I recall that the standard magic square had 5 in the center with the sum n = 15. Add 3 to every square, and we get the numbers 4 through 12 with 8 in the center. Their sum = 72, and id we divide by 3, n = 24. Ed Gray

If we go backward and forward in the grid from 8 , rest of the numbers are 7,6,5, 4 and 9,10,11 and 12 . If we add all of them we have 16*9/2=72 . Hence each row or column or diagonal adds upto 72/3 = 24

Prolog program to derive solution to magic square. just ask (type) ?- g(X).

soma1([A,B,C,D,E,F,G,H,I],N):- N is A + B + C. soma2([A,B,C,D,E,F,G,H,I],N):- N is D + E + F. soma3([A,B,C,D,E,F,G,H,I],N):- N is G + H + I. soma4([A,B,C,D,E,F,G,H,I],N):- N is A + D + G. soma5([A,B,C,D,E,F,G,H,I],N):- N is B + E + H. soma6([A,B,C,D,E,F,G,H,I],N):- N is C + F + I. soma7([A,B,C,D,E,F,G,H,I],N):- N is A + E + I. soma8([A,B,C,D,E,F,G,H,I],N):- N is C + E + G.

lista([4,5,6,7,8,9,10,11,12]). verifica(L,N):- soma1(L,N), soma2(L,N), soma3(L,N), soma4(L,N), soma5(L,N), soma6(L,N), soma7(L,N), soma8(L,N).

go(N):- lista(L), permutation(L,Ls), [A,B,C,D,E,F,G,H,I] = Ls, E = 8, verifica([A,B,C,D,E,F,G,H,I],N), faz([A,B,C,D,E,F,G,H,I]).

faz([A,B,C,D,E,F,G,H,I]):- write([A,B,C]), nl, write([D,E,F]), nl, write([G,H,I]), nl.

The rule for solving magic squares with 1 digit(the digit has to be in the center) is that 3 times the middle digit or n as you have to find.