A classical mechanics problem by Pankaj Joshi
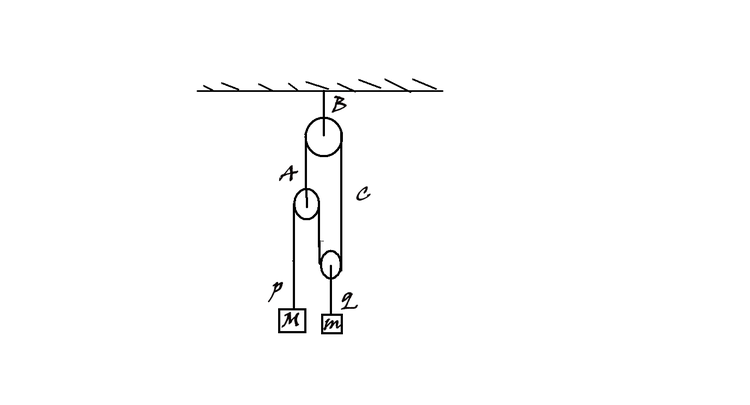 The arrangement shown in figure has
2
masses
M
=
4
kg
and
m
=
1
kg
. The magnitude of acceleration of mass
M
and
m
is
p
and
q
respectively. The value of
p
+
q
is
(
g
=
1
0
m/s
2
)
:
The arrangement shown in figure has
2
masses
M
=
4
kg
and
m
=
1
kg
. The magnitude of acceleration of mass
M
and
m
is
p
and
q
respectively. The value of
p
+
q
is
(
g
=
1
0
m/s
2
)
:
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
T1=T2.. Why sir?
Log in to reply
Note that the string passing over A has tension T on both sides of A. So the string connected to A(to A's center) will have tension 2T as A is being pulled from both sides. Now note that it is the same string, so tension should be same. 2T=T which can be possible only when T=0, this results in blocks' free fall.
Log in to reply
Why should tension be the same,why is the pulley necessarily in equilibrium?
Log in to reply
@Lawrence Mayne – When mass of the pulleys is not mentioned, we take them to be massless by convention. Massless bodies have no net external force .So tension should be same.
As mentioned above by me, only one tension T1 is relevant. If T2 is the tension on string connecting m to the pulley, we are not interested in it. As Pankaj Joshi has proved, T1 = 0.
Observe that the string that connects those pulleys are the same string. Since the string is massless then it must have the same tension. We see that on the point A, the equation for the pulleys is T − 2 T = 0 then we have T = 0 Since the tension of the string is zero then we have the acceleration of those mass are equal to g , that is 1 0 m / s 2 . Then the sum of those accelerations are p + q = 1 0 m / s 2 + 1 0 m / s 2 = 2 0 m / s 2
Let T1 be the tension in the string attached to M an T2 be the tension in the string attached to m. Now apply Newton's law to the system. Mg - T1 = Mp. T2 - mg = mq. Since the pulleys are mass less,
2T1 - T2 = 0 So T1 = T2 = 0 and p = q = g.