Which constraint would you use?
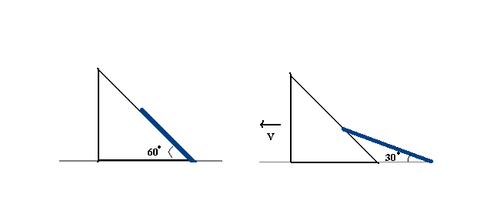 A thin rod of mass
m
=
1
kg and length
l
=
1
m is placed along the hypotenuse side of a wedge lying on a friction less floor having mass
M
=
5
kg and angle
6
0
°
. At
t
=
0
the system is released from rest. Both the objects are free to move. Find the speed of the wedge when the rod makes an angle
3
0
°
with the floor.
A thin rod of mass
m
=
1
kg and length
l
=
1
m is placed along the hypotenuse side of a wedge lying on a friction less floor having mass
M
=
5
kg and angle
6
0
°
. At
t
=
0
the system is released from rest. Both the objects are free to move. Find the speed of the wedge when the rod makes an angle
3
0
°
with the floor.
The answer can be expressed as b a ( 3 − 1 ) . Find a + b .
Notes
- Take g = 1 0 m / s 2
I got this question from Tanya Sharma .
The answer is 157.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Tanya helped me in finding the answer too. :) The solution is not entirely mine.
Log in to reply
Really Interesting ! I mean using Vectors ! Finally still I solved it by using components of velocity !! As I told you earlier , I found my mistake , I was making an mistake by taking 30 degree instead of 60 in 2nd constrained :)
Log in to reply
I solved this using the concept of instantaneous axis of rotation, that greatly reduced the work of solving this problem.
Log in to reply
@Ronak Agarwal – Yes! Totally Agreed , That reduce much calculation !
One Can also solved This by Letting velocity of rod as V x , V y , ω .
and then use constrained V B , V e r t i c l e ( n e t ) = 0 V r e l a t i v e , ( C o m m o n N o r m a l ) = 0 V A , r o d , ( a l o o n g l e n g t h ) = V B , r o d , ( a l o o n g l e n g t h ) ∑ p = 0 ( x − a x i s ) ∑ E n e r g y = c o n s t . .
And This is interesting that we got 5 equations But where as we have only 4 variables :)
@Ronak Agarwal – Could you please post your solution. :)
I think finding component by using vector is easier . What do you think?
I am in class 10 at present and I am in confusion which subject combination should I take in class 11. :( What do you suggest? What were your subject combination in class 12?
Log in to reply
@Satvik Pandey – did you mean optional subjects with PCM ? If yes , Then Actually it's your choice ! But in my opinion if you had genuine interest in Computer field then go for computer Science ! ( Because it is only based on your interest ) And believe me it is very interesting subject !
Or if you don't have much interest , and if you r thinking of your 12th board % then Choose IP ( Information Practices ) (Yes another computer subject ) as your optional subject Because it is full scoring subject with very Least effort ! Otherwise Physical Edu. is also good Option !! Choice is yours :)
And I had passed 12th with PCM + IP ( obviously English also ) :)
Log in to reply
@Deepanshu Gupta – Thanks Deepanshu. :)
What do think about choosing hindi or sanskrit as an additional subjects. I am focusing on 12 percentage. I am in search of subject which is scoring and which requires pretty much less attention.
Log in to reply
@Satvik Pandey
–
Well I Dont say anything about Sanskrit ( Although My Mom is Sanskrit Teacher :) ) But I always Hate it !
And In My opinion Hindi is not an much scoring subject Instead of Hindi I suggest you to choose IP . Because My friends Who choose Hindi didn't score that much in that (My friend who is in IIT kanpur Now Got only 88 although He is Brilliant guy And Topper of our school ) ! Where as an dumb guy Like me got 96 in IP , and also I hardly attend my IP class :) , Also Course of IP is almost same for 11th and 12th So it helps much !!
I'am Not saying that it is impossible to score in hindi But Really it is difficult as my friend Told me always !!
And Physical education is also good subject for Scoring !!
In Last I only suggest you For IP ( Since it is Scoring subject without any effort )
but choice is yours :)
Log in to reply
@Deepanshu Gupta – Thanks for help, Deepanshu! My mother is a chemistry teacher but I too hate chemistry. :D
You are not a dumb guy bro. I think you are highly underestimating yourself.
I will too go for IP if I would get that subject in combination with PCM in a school near by my locality. :)
Log in to reply
@Satvik Pandey – Me too !! (Don't Like Chemistry much :)) And Gud Luck to ur Future . :)
From where exactly you or your friend got this question from can you please tell me, cause I have created exactly the same question and posted in on brilliant some days ago. @satvik pandey
Log in to reply
Well I got this from Tanya on a forum. I don't know where she got this from.
I also got ω=8V, but when I plug that into the CoE equation, I keep getting 1/2 5V^2+1/2 (5V)^2+1/2 1/12 (8V)^2=5/2(sqrt(3)-1), which gives me a=15, b=106. Can someone please tell me where I'm going wrong?
I used 4 concepts to make 4 equations of 4 variables.
The variables are : vertical velocity of rod , horizontal velocity of rod , angular velocity of rod , horizontal velocity of wedge!
Concepts employed in my method are
-
Conservation of Momentum along horizontal direction .
-
The Right end of rod has no net vertical velocity .
-
The contact points have same velocity along common normal .
-
Energy Conservation! . :)
The problem becomes quite easy if we apply some simple geometry.Note that v=rate of change of displacement.so once we can get these displacements we can differentiate wrt time.these displacements can be easily found geometrically.but its better that we find the displacements in both x and y directions.note that if the wedge has a velocity v then the com of the rod has v ( x ) = − 5 v .but then the technique discussed above(of differentiation)yields ( v + 3 w L / 4 ) = v ( x ) .equating gives w = − 8 v / L .Now we may use energy conservation KE(of system of wedge and rod)= ( 1 / 2 ) I w 2 + ( 1 / 2 ) m ( 5 v ) 2 + ( 1 / 2 ) m ( 8 v ) 2 + ( 1 / 2 ) M v 2 and equating it to the loss of gravitational potential energy yields v = √ 1 5 / 1 4 2 ( √ 3 − 1 ) .I don't know how to post solutions as above but this way was quite simple.
To arrive at equation 2 I did the following.1)-Let's say that the wedge moves a distance x .The leaning rod at that infant makes an angle @ with the horizontal.Let the bottommost end of the rod be at a distance y from the wedge.2)Using geometry we can find the displacement of com in the X direction.This is of the form X = x − ( y − L / 2 c o s @ + L / 4 ) .where y can be easily computed by using sine law. y / s i n ( 6 0 − @ ) = L / s i n 1 2 0 .So d X / d t = ( d x / d t ) − ( d y / d t ) − ( L / 2 ) s i n @ d @ / d t .But d @ / d t = w .and we have y so we can compute ( d y / d t ) and d x / d t is nothing but speed of wedge.And from momentum conservation d X / d t = − 5 v .Now setting in the eq and @ = 3 0 yields w = − 8 v / L .So the vertical velocity is v ( ∗ ) = 8 v
Good approach...👍👍👍
@Sibasish Mishra BTW you too did in the same way??Usually I follow this technique when there is something that is evident geometrically.Or Instantaneous axis of rotation.
Log in to reply
I followed the instantaneous axis of rotation..
Log in to reply
Ohk!good...... I have added the way to my solution.
I am feeling that yr method can be really useful to solve in short , please do make a sketch of your method to get that 2nd eq and post the pic...
I solved it using 3 main concepts
-
conservation of energy
-
Rod right down point don't have vertical velocity
-
The contact point's velocity along direc perpendicular to incline is same for both!
And of course momentum conservation!
Log in to reply
OK I will post it. But Solutions with basics are always the best(as you did)👏👏
Hey can you just say how to upload pics captured from phone..😀😀
OK so I have added that to my solution.This method works well in many instances where there is constrainted motion and some geometry that's quite apparent.
Log in to reply
Okay , so your solution differs with mine on the context that instead of there common be velocity along normal you used this method to find an equation ! Rest all is same ... Length of both of our solution are nearly the same! :)
You forgot to write the energy due to vertical velocity of rod in yr sol!
Log in to reply
@Aniket Sanghi – Oh yes.I forgot.Have added
Let V be the speed of the wedge and v be the velocity of the CoM of the rod.
Clearly no external force act in the horizontal direction on the system
So M V = m v x ................(1)
By the conservation of the energy-
2 m g l ( s i n ( 6 0 ) − s i n ( 3 0 ) ) = 2 1 M V 2 + 2 1 m v 2 + 2 1 I ω 2
Now here comes the main part of the solution-- img
img
This figure shows the velocity of point A, B ,C relative to earth and relative to point C. C is the CoM of the rod.
So V A / C = − 2 l ω s i n θ i ^ − 2 l ω c o s θ j ^
and V B / C = 2 l ω c o s θ j ^ + 2 l ω s i n θ i ^
As V B C = V B − V C
Using this in vertical direction we will get
2 l ω c o s θ j ^ = 0 − V C j ^
V C j ^ = − 2 l ω c o s θ j ^
So V c = m M V i ^ − 2 l ω c o s θ j ^
(got this -- m M V i ^ from conservation of momentum in X direction)
Also V A C = V A − V C
So V A = ( m M V − 2 l ω s i n θ ) i ^ − l ω c o s θ j ^
Also as the the point A of the rod remains in the contact with the wedge so the velocity of the point A and wedge perpendicular to the contact surface should be equal.
Now velocity of the wedge perpendicular to the contact surface is V s i n ( 6 0 )
Now we have to find the velocity of the point A perpendicular to the contact surface. For this we will use dot product approach. For this we have to find the unit vector perpendicular to the contact surface.
From the figure unit vector perpendicular to the contact surface is
B = − 2 3 i ^ − 2 1 j ^
And V A = ( m M V − 2 l ω s i n θ ) i ^ − l ω c o s θ j ^
V A ⋅ B = V A B c o s ( α ) where α is the angle between V A and B)
or V A c o s ( α ) = B V A ⋅ B
Also V A c o s ( α ) is the component of the V A in direction perpendicular to the contact surface.
So V s i n ( 6 0 ) = { ( m M V − 2 l ω s i n θ ) i ^ − l ω c o s θ j ^ } ⋅ { − 2 3 i ^ − 2 1 j ^ }
V s i n ( 6 0 ) in the LHS is the velocity of the wedge perpendicular to the contact surface.
On putting the values we will get 2 − 5 3 V + 8 3 3 ω = 2 V 3
or ω = 8 V
As V c = m M V i ^ − 2 l ω c o s θ j ^
On putting ω = 8 V in this equation we will get
V C = 3 7 V
On putting this value in the equation that we got from the conservation of the energy we will get
1 5 ( 3 − 1 ) = 1 4 2 V 2
or V = 1 4 2 1 5 ( 3 − 1 )
So a + b = 1 4 2 + 1 5 = 1 5 7 .
The most difficult part of the question is to find relation between V and ω .