A New Earth!
 A strangely spherical planet called
Golplan
was found and an initial test confirmed that the planet was made of homogeneous gold (WoW!). A group of scientists along with some workmen who were skilled in excavations was send in a probe to
Golplan
. A narrow trial shaft was bored from point A on its surface to the centre of the planet. At that point, an accident occurred when one of the workers fell off the surface of the planet into the trial shaft. He fell, speeding as he got nearer to the centre, and finally reached
, where he died. However, the work was continued and the group started excavation of gold, forming a spherical cavity of diameter
in the planet, as illustrated.
A strangely spherical planet called
Golplan
was found and an initial test confirmed that the planet was made of homogeneous gold (WoW!). A group of scientists along with some workmen who were skilled in excavations was send in a probe to
Golplan
. A narrow trial shaft was bored from point A on its surface to the centre of the planet. At that point, an accident occurred when one of the workers fell off the surface of the planet into the trial shaft. He fell, speeding as he got nearer to the centre, and finally reached
, where he died. However, the work was continued and the group started excavation of gold, forming a spherical cavity of diameter
in the planet, as illustrated.
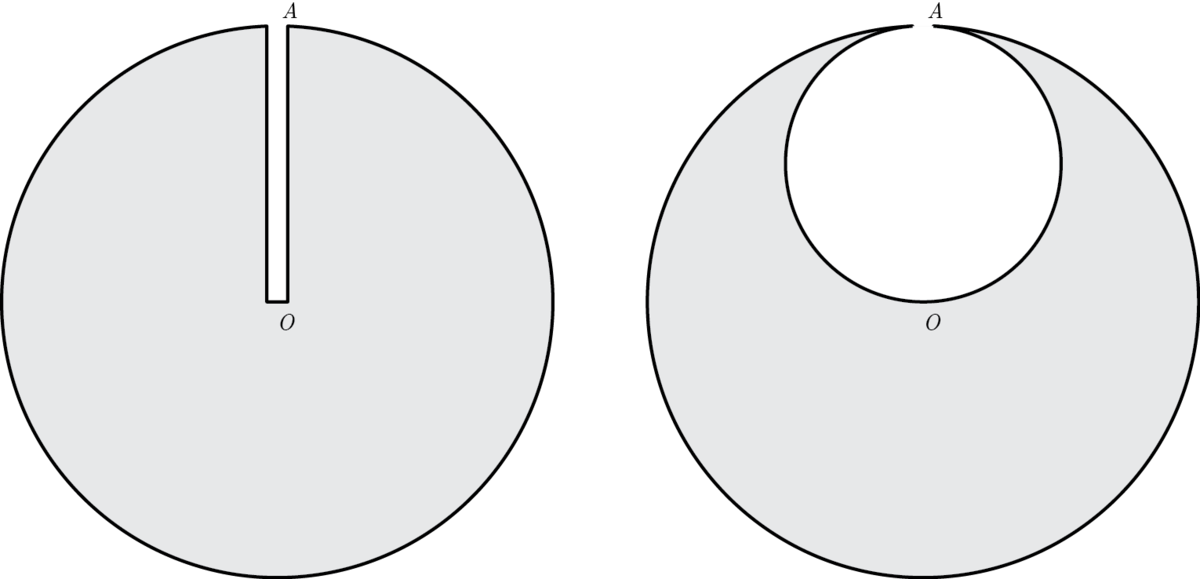
Then a second accident occurred - another workman similarly fell from the point A to point and died. An expert scientist was asked to calculate the ratio of the impact speeds and the ratio of times taken to fall from to by the two unfortunate workers.
If we denote and , find the value of .
Assume that the volume of the narrow trial shaft to be negligible.
The answer is 0.78539816339744830961566084582.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First of all, from laws of gravitation, we know, a ( r ) a = r 2 G M ( r ) = 3 r 2 4 ρ G π r 3 = 3 4 ρ G π r
Note one thing that the above equation represents that of a Simple Harmonic Motion. So, ω = 3 4 ρ G π and Amplitude A = R T 1 v 1 = 4 T = 4 ω 2 π = 4 1 ρ G 3 π = ω A = 2 R 3 ρ G π
Now comes the tricky part. Let's investigate...
Take the centre of the cavity to be C and the vector from C to O be c and the radius vector to any arbitrary point be r so that the radius vector of that point to the centre of the cavity becomes c + r .
Now, since the cavity is removed from the whole mass, we can take the negative mass system corresponding to the cavity. Also, the accelerations will be proportional to the radius vectors and the constant of proportionality is ω 2 . Thus, a = ω 2 ( − r ) + − [ ω 2 ( − { r + c } ) ] = ω 2 c = ω 2 2 R
The acceleration here is thus a constant.
So, T 2 v 2 = ω 2 = ρ G π 3 = ω R = 2 R 3 ρ G π
Thus, x = T 2 T 1 = ρ G π 3 4 1 ρ G 3 π = 4 π
And, y = v 2 v 1 = 2 R 3 ρ G π 2 R 3 ρ G π = 1
∴ y x = 4 π ≈ 0 . 7 8 5 4