New way to find square root
Given that 1234321 is a perfect square, quickly find the value of
1 2 3 4 3 2 1 .
The answer is 1111.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
Can you explain why this pattern works?
Also, note that the pattern "fails" for n > 9 . Or at least, the pattern is no longer as pretty.
Log in to reply
( 1 + 1 0 + 1 0 0 + . . . . . . . . . + 1 0 n ) 2 = 1 2 + 1 0 2 + . . . . . . . . + 1 0 2 n + 2 ( 1 . 1 0 + 1 . 1 0 0 + . . . . . + 1 0 . 1 0 0 + 1 0 . 1 0 0 0 + . . . . . . . . . . . + 1 0 n − 1 . 1 0 n )
And I can't think of any better reason behind it failing after n = 9 except our being unable to define it for 2 digit numbers.
Log in to reply
Hm, I'm not sure how that explains the pattern. I do not immediately see how 1234321 falls out of it.
The pattern is no longer as pretty in the sense that
ten 1 ′ s 1 1 1 1 1 1 1 1 1 1 2 = 1 2 3 4 5 6 7 9 0 0 0 9 8 7 6 5 4 3 2 1
Most people would be "expecting" 1234567890987654321.
The reason why it doesn't work is because the 0 is actually a 10, and so it carries over to the 9, and 9 + 1 = 1 0 and so it caries over to the 8, giving us 9 0 0 instead of 8 9 { 1 0 } .
Yes i did it by pascal's triangle and yours one , but i think Sir would be happy to see a good algebric proof @Satvik Golechha
Log in to reply
@U Z – How do you use a pascal's triangle, could someone please explain? Thanks
You can try this method to find the square root of any other number. And Thank You For Your Correction and Suggestion
Sir,because when we multiply by common method i.e one digit leaving other and as it's all digit is one.Also when at middle most digit it starts making a stair without base. . Now if no. Of one is more than 9 it generates carry which creates deviation......
I will try to use a combinatorics approach to prove the sequence (I will neglect the case n > 9 for now) . However many 1's you have the 1st digit in the result will always be 1 because it is obtained by multiplying the biggest powers of 10 together once. For the next digit we obtain 2 because two 1's are involved into multiplication on each side. It is easy to see that the number of, powers of 10, used in multiplication determines each digit. The reason that each result is palindromic is that 111.... is symmetric, so the multiplication is also symmetric. After n > 9 some of digit values carry over. [This can be seen if you write out the two numbers and join up the powers of 10's that you are multiplying together.]
It is pascal triangle pattern.
Log in to reply
1 2 1 , 12321 ... This is not pascal's triangle. Saying so is misleading others.
from the rules of divisibility of 11, it is obvious that 1234321 is a multiple of 11 (by alternating sum: 1-2+3-4+3-2+1 = 0 )
1 2 1 1 2 3 4 3 2 1 = 1 0 2 0 1 which you can recognize as the square of 101. Because 1 0 2 0 1 = 1 0 0 0 0 + 2 0 0 + 1 = 1 0 0 2 + 2 ( 1 ) ( 1 0 0 ) + 1 = ( 1 0 0 + 1 ) 2
1 1 × 1 0 1 = 1 1 1 1
It is easy to find the square root of a big number.
The square root of a number with n digits will contain n/2 or n+1/2 digits.
The unit place of square root of a perfect is 0,1,4,5,6 or 9.
The square root of given number is a 4 digit number whose unit place is 1 or 9.(because the last digit of the number is 1)
The number lies between square of 1110 and 1120. The possible values are 1111 or 1119.
The square of 1110 is 1232100 and 1120 is 1254400. The number 1234321 is closer to 1232100 as compared 1254400. Therefore the square root is closer to 1110.
So the correct answer is 1111. This method is also valid for smaller number.
This approach requires knowing that 1234321 is a perfect square. Let me edit that into the question.
how do u conclude that the square root lies b/w 1110 and 1120 ? can u explain ?
Log in to reply
I think that he calculate nearest values. Square of 111 and 112 and then multiplied each by 10. The number came in between.
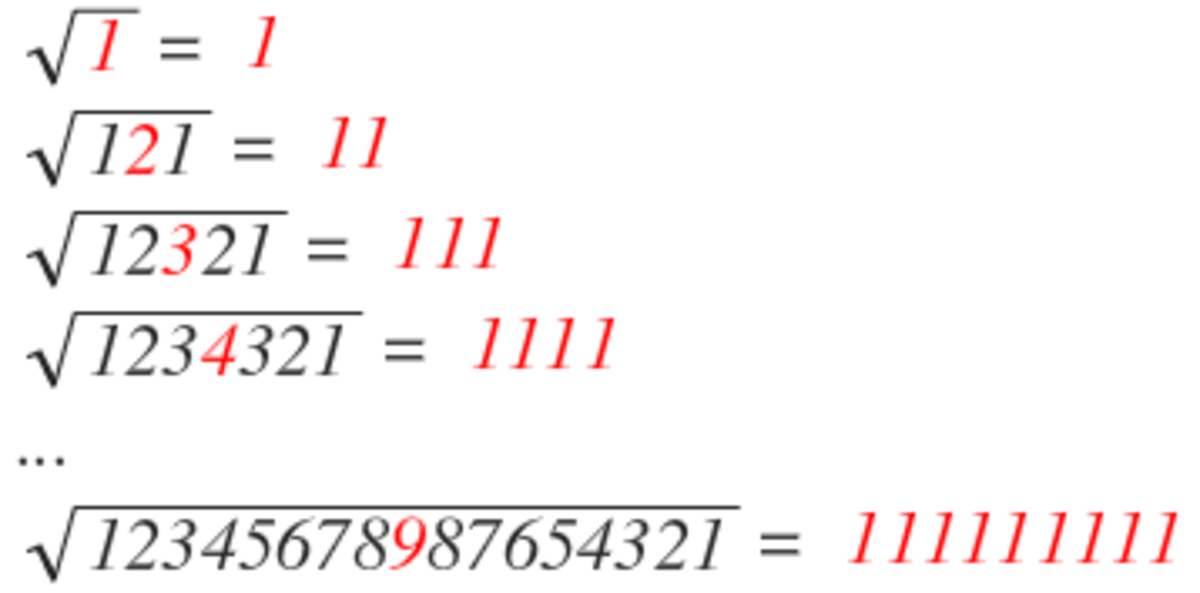Can you see the pattern?
Checking for divisibility by small primes, we can see that 11 divides our number. Therefore, 121 must also divide it. We can then see that 1 2 3 4 3 2 1 = 1 2 1 ( 1 0 4 + 2 0 0 + 1 ) = 1 1 2 ( 1 0 0 + 1 ) 2 (because x 2 + 2 x + 1 = ( x + 1 ) 2 . The answer is 1 1 ⋅ 1 0 1 = 1 1 1 1 .
root of 1234321 = root of 121 * 10201 = 11 * root of 10201,
10201 = 10,000 + 200 + 1 = a^2 + 2ab + b^2 = 101^2,
root of 10201 = root of 101^2 = 101,
so answer = 11 * 101 = 1111
Here's a lesser known way to find the solution. Using this, you can find root of any integer with high precision.
Moderator note:
Can you explain what you are doing?
For coefficients, count how many ways there are of obtaining each power-of-ten product from the two brackets.
1 1 1 1 2
= ( 1 0 0 0 + 1 0 0 + 1 0 + 1 ) 2
= 1 × 1 0 0 0 0 0 0 + 2 × 1 0 0 0 0 0 + 3 × 1 0 0 0 0 + 4 × 1 0 0 0 + 3 × 1 0 0 + 2 × 1 0 + 1 × 1
= 1 2 3 4 3 2 1 .
We observe:
1^2= 1
11^2 = 121
111^2 = 12321
1111^2 = 1234321
√1234321=√10^4×123.4321=100√123.4321. 11×11=121,,,,12×12=144 so √123.4321is between 11&12 assume 11.15^2=121+.0225+3.3=124.3225. assume 11.11^2=121+.0121+ 2.42=123.4321### so √1234321=100×11.11=1111####
http://www.wolframalpha.com/input/?i=sqrt%281234321%29
we know
1 1 2 = 1 2 1
1 1 1 2 = 1 2 3 2 1
we can see a sequence
therefore,
1 2 3 4 3 2 1 = 1 1 1 1 2
1 1 1 1 1 2 = 1 2 3 4 5 4 3 2 1
:
: