An algebra problem by diali kundu
If a+b=6,then what is the greatest value of ab?
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
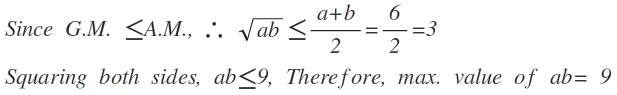
Can you tell us why there is a b instead of ab
Log in to reply
This type of solution I was expecting. Root ab is the geometric mean .
Hmm... I dont see why a=b?
a + b = 6
1 + 5 = 6 => (1)(5) = 5
2 + 4 = 6 => (2)(4) = 8
3 + 3 = 6 => (3)(3) = 9 (Hence Greatest value of ab)
How do you know that a and b are positive integers
Log in to reply
If you take negative it will not give Greatest value.
For example: -3 + 9 = 6 but (-3)(9) = -27 (Not a greatest Value)
Or,
Two Negative numbers will break the Rule i.e. a + b = 6 .
Log in to reply
And how do you know that a and b are integers, can you prove that that why only 3+3 gives the maximum value?
Log in to reply
@Kushagra Sahni – It is quite obvious from question !
Log in to reply
@Syed Baqir – You are not understanding, I am asking why only a=b=3 gives maximum value of a and b. Why is 9 the maximum value of ab. Aren't there any other real values of a and b which give a value of ab greater than 9. Prove that 9 is the maximum value of ab.
Log in to reply
@Kushagra Sahni – Well, its obvious because
4 + 2 = 6 BUT (4)(2) = 8 < 9
5 + 1 = 6 But (5)(1) = 5 < 9
Log in to reply
@Syed Baqir – Prove that 9 is the largest value for ab if a and b lie over all real numbers. Not only integers.
Log in to reply
@Kushagra Sahni – a + b = 6 , ab =9
a = 6 -b , b = 6 - a
(6 - b)(b) = 9 => − b 2 + 6 b − 9 ⟶ ( b − 3 ) 2 = 0
→ b = ± 3
Hence we take Positive because negative is not Possible as it will not obey a + b = 6 .
You cannot assume that there is any other greatest value!!
Log in to reply
@Syed Baqir – Lol, how are you using that the maximum value is 9? That's what you have to prove. You can't take ab =9. You only know that a+b is 6 that's all. Now prove that maximum value of ab is 9.
Log in to reply
@Kushagra Sahni – Can you find any other value that is maximum,
If you read what I said you will find that there is no other value which gives more than 9 there is no such proof because it is obvious as any other value will break
a + b = 6
Only possible answer is 3 by trail and error .
Log in to reply
@Syed Baqir – When did I say that 9 is not correct. Of course it is but I was asking you to prove that. Of course there is a proof and what if a and b are not integers, you are only testing for integers and you got your answer by trial and error. Hint for the proof is AM-GM inequality.
Log in to reply
@Kushagra Sahni – Ohh , ok we have someone posted the proof luckily !
@Kushagra Sahni – see, the real solution is; (a-b)2 is greater than/equal to 0 or, (a+b)2-4ab is greater than equal to 0 or, (6)2 -4ab is greater than equal to 0 or, 36 is greater than equal to 4ab or, 4ab is less than equal to 36 or, ab is less than equal to 36/4 or, ab is less than equal to 9.
so, the greatest value of ab is 9.