Two Pairs of Matching Hearts
Dwight has 7 cards, and he places them randomly in a row. Then Dave places the same cards (from a different deck) in a random order just underneath Dave's row.
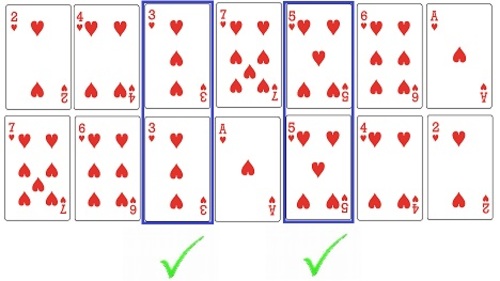
Once Dwight has placed his cards, how many ways can Dave place his cards such that they end up so that exactly two cards match (like in the figure above)?
The answer is 924.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The probability P ( m , n ) that with m cards dealt there are precisely n matches, (where 0 ≤ n ≤ m − 2 or n = m ), is
P ( m , n ) = m ! ( n m ) × ! ( m − n ) = ( m − n ) ! n ! ! ( m − n ) .
For large enough m we have P ( m , n ) ≈ n ! × e 1 , which is a good approximation even here as P ( 7 , 2 ) = 5 ! 2 ! ! 5 ≈ 0 . 1 8 3 3 3 and 2 e 1 ≈ 0 . 1 8 3 9 4 , a 0.33% error. (For m = 5 2 the approximation is good to 67 decimal places.) I still find it a bit un-intuitive that once you get past m = 7 or so P ( m , n ) is pretty much independent of m .
Log in to reply
Interesting indeed... Perhaps the making of another problem?
Log in to reply
Perhaps. :) Another one I'm considering is where there is a third deck, from which the 7 cards are dealt in a third row, and the question is to find the probability P 3 ( 7 , 1 ) that there is precisely one match through all three rows, (or generalize to n matches). I(Strictly pairwise matches are allowed, but just one thrice-wise is.) I'm getting P 3 ( 7 , 1 ) ≈ 0 . 0 8 5 8 , which seems reasonable, but my approach doesn't yield n = 0 ∑ 5 P 3 ( 7 , n ) + P 3 ( 7 , 7 ) = 1 , so I suspect my method is flawed. I find that P 3 ( 7 , 0 ) ≈ e 2 − e 2 1 ≈ 0 . 6 0 0 , but that seems a bit low ....
Log in to reply
@Brian Charlesworth – Interesting... Lemme ponder that one a bit...
@Brian Charlesworth – Hmmm... I wonder if we can start with a 3 card deck. i.e. P 3 ( 3 , 1 ) , and work our way up... :-/
There are ( 2 7 ) ways to pick which columns match. Then there are ! 5 ways to arrange the remaining 5 columns so that they don't match, where ! n is the derangement formula for n objects.
This gives:
( 2 7 ) ⋅ ! 5 = 2 1 ⋅ 4 4 = 9 2 4