A Perturbed Orbit

Classical Mechanics Level 5

Particle $1$ has mass $m_1 = 1$ and is fixed in place at position $(x_1, y_1) = (0,0)$ . Particle $2$ has mass $m_2 = 1$ and is fixed in place at position $(x_2, y_2) = (30,0)$ . Particle $3$ has mass $m_3 = 1$ and is free to move under the influence of the gravitational forces from the other two particles.

At time $t = 0$ , the position and velocity of Particle $3$ are as follows:

$(x_3, y_3) = (1,0) \\ (\dot{x}_3, \dot{y}_3) = (0,1)$

Note that in the absence of Particle $2$ , Particle $3$ would undergo uniform circular motion about the origin. Let $r_{max}$ be the largest distance of Particle $3$ from the origin between $t = 0$ and $t = 50$ .

What is $(r_{max} - 1)$ ?

Bonus: Make an $xy$ scatter plot of the trajectory of Particle $3$ . Are you surprised by the extent of the orbital deviation, given that the force from Particle $2$ is only about one thousandth the strength of the force from Particle $1$ ?

Details and Assumptions:
1) Universal gravitational constant $G = 1$
2) All quantities are in standard $SI$ units

The answer is 0.0732.

3 solutions

Karan Chatrath
Jan 10, 2021

Continuing my effort to avoid derivative crunching by hand.

Position of particle 3 at a general time is $\vec{r}_3=(x,y)$ and velocity is $\vec{v}_3=(\dot{x},\dot{y})$ . Potential energy of the system is:

$V = -Gm^2\left(\frac{1}{\lvert \vec{r}_3-\vec{r}_1\rvert} + \frac{1}{\lvert \vec{r}_3-\vec{r}_2\rvert} + \frac{1}{\lvert \vec{r}_2-\vec{r}_1\rvert}\right)$

The third term can be ignored as well as that is a constant. Kinetic energy of the system is:

$T = \frac{m}{2}\left(\dot{x}^2 + \dot{y}^2\right)$

Applying Lagrangian mechanics:

$\ddot{x} = -\frac{\partial V}{\partial x}$ $\ddot{y} = -\frac{\partial V}{\partial y}$

The trajectory of the particle is:

If the particle 2 was absent, the trajectory would have been the expected elliptical closed orbit. The presence of mass 2 causes the mass 3 to deviate from this original trajectory. In general, the three body problem yields more complicated motions than the two-body problem.

clear all
clc

% Initial conditions:
x(1)    = 1;
y(1)    = 0;

dx(1)   = 0;
dy(1)   = 1;


% Time initialisation:
dt      = 1e-5;
tf      = 50;
t       = 0:dt:tf;

% Loop for numerical integration:
for k = 1:length(t)-1

    % Distance from origin:
    D(k)   = norm([x(k);y(k);0]);

    % Equation of motion:
    ddr       = -Potential_Gradient([x(k);y(k)]);
    ddx       = ddr(1);
    ddy       = ddr(2);

    % Numerical integration: Semi implicit Euler:
    dx(k+1)   = dx(k) + ddx*dt;
    dy(k+1)   = dy(k) + ddy*dt;

    x(k+1)    = x(k) + dx(k+1)*dt;
    y(k+1)    = y(k) + dy(k+1)*dt;
end

ANSWER     = max(D);
% ANSWER - 1 = 0.0732

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function V = Potential_Energy(X)

x       = X(1);
y       = X(2);

r1      = [0;0;0];
r2      = [30;0;0];
r3      = [x;y;0];


G       = 1;
m       = 1;

V       = -G*m^2*(1/norm(r3 - r1) + 1/norm(r3 - r2));

end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function dV = Potential_Gradient(X)

x       = X(1);
y       = X(2);

eps     = 1e-10;

% Partial derivative wrt x:
dVx     = (Potential_Energy([x+eps;y]) - Potential_Energy([x;y]))/eps;

% Partial derivative wrt y:
dVy     = (Potential_Energy([x;y+eps]) - Potential_Energy([x;y]))/eps;

% Gradient vector:
dV      = [dVx;dVy];

end

I was also wondering about the stability of the solar system. Do the gravitational interactions between planets make the orbits unstable, over a very long period of time?

Steven Chase - 5 months ago

The question is difficult for me to answer. The way I would rigorously attempt this is by creating a simulation model of multiple planets based on Netwon's law of gravitation and simulate that for very long periods of time, to get some preliminary insights. Instead of doing that, I asked Google and ran into the following article. It gives a semi-analytical, numerical and historical perspective on the problem of orbital stability. Interesting first read.

http://www.scholarpedia.org/article/Stability of the solar system

Karan Chatrath - 5 months ago

@Steven Chase haha Newton had the same question. He, however, believed that the solar system needed divine intervention to keep from propelling into disaster.

Laplace actually wrote a treatise about the same issue. Mécanique Céleste is regarded one of the most important books in physics. He proved that planets would make only very small deviations from their orbit, and this was a huge finding in terms of answering the stability of the solar system question.

It will probably be very stable for the next few billion years.

Krishna Karthik - 5 months ago

Indeed, it sounds like the sun's transformation into a red giant will be the more pressing issue.

Steven Chase - 5 months ago

@Steven Chase – By then, I have full confidence that we would have become a type 3 civilisation. Or, we could have stayed on Earth and some other natural disaster would have wiped us out, just like the dinosaurs.

Krishna Karthik - 4 months, 4 weeks ago

I just realised that you mention that $G=1$ and then mention that the unit system followed is SI. I think this is a contradiction. If the gravitational constant is scaled, then effectively, the unit system changes. The magnitude of $G$ in SI units is $\approx 6.67 \times 10^{-11}$ .

Karan Chatrath - 4 months, 4 weeks ago

I would really like to disregard units altogether. They are nothing but an inconvenience. But people complain when I do that.

Steven Chase - 4 months, 4 weeks ago

Oh, I understand the intent of you doing so, and I agree with it. I did the same in my simple relativity problems when I scaled the speed of light to unity. I am just saying that it would be adequate to mention that 'The unit system in consideration is one where the gravitational constant is normalized to 1, for numerical convenience'. Or simply stating that $G=1$ should suffice. Just a suggestion.

Karan Chatrath - 4 months, 4 weeks ago

@Karan Chatrath – Indeed, I think I'll just go back to having numbers without specifying any particular unit system. The implied instruction is to assume that the equations take their "standard forms".

Steven Chase - 4 months, 4 weeks ago

Krishna Karthik
Jan 13, 2021

Nice problem. At first, I tried to animate to see what would happen, but I couldn't really see anything visually. However, when I zoomed through and traced the orbit, it became more apparent.

I had to compress and optimize the file a lot for it to appear on this solution.

As you can see in the animation, the orbit deviates at the top and the bottom. This is much more apparent as time progresses. If you want to see the other particle on the right, just change the figure dimensions.

It is kind of surprising that a body that far away impacts the orbit like that. Here's some code; if you have matlab, please run it; you can see the animation of the perturbed orbit. It looks pretty cool.

clc;
close all;
clear;

%% Initialisation
time = 0;
deltaT = 10^-5;

m0 = 1;
m1 = 1;
m2 = 1;

G = 1;

x = 1;
y = 0;

xDot = 0;
yDot = 1;

times = [];
positionX = [];
positionY = [];

maximumDistance = hypot(x,y);

count = 0;

%% Simulation
while time <= 50
%% lists for animation    
    if mod(count,1000) == 0
        times = [times; time];
        positionX = [positionX; x];
        positionY = [positionY; y];
    end
 %% Computation   
    length1 = hypot(x,y);
    length2 = hypot(30-x,y);

    %update the maximum distance if the distance is greater than current 
    if length1 > maximumDistance
        maximumDistance = length1;
    end

    %unit vector directions of forces
    u = [-x/length1 -y/length1];
    v = [(30-x)/length2 -y/length2];

    %gravitational forces
    Force1 = u*(G*m0*m1)/length1^2;
    Force2 = v*(G*m1*m2)/length2^2;

    %total force
    totalForce = Force1 + Force2;

    %% numerical integration
    xDotDot = totalForce(1)/m1;
    yDotDot = totalForce(2)/m1;

    xDot = xDot + xDotDot*deltaT;
    yDot = yDot + yDotDot*deltaT;

    x = x + xDot*deltaT;
    y = y + yDot*deltaT;

    time = time + deltaT;
    count = count + 1;
end

%% answer
disp("Answer: " +num2str(maximumDistance-1));
pause(2);

%% Animation
particle1 = [0 0];
particle2 = [30 0];

axis(gca, "equal");
axis([-4 35 -4 4]);
grid on;

%fixed bodies
viscircles(particle1, 0.5);
viscircles(particle2, 0.5);

i = 1;

while i < length(times)
    %animating moving body
    positionVector = [positionX(i) positionY(i)];
    title("time: " + num2str(times(i)) + " s");    

    Mass1 = viscircles(positionVector,0.5);
    line([positionX(i) positionX(i+1)],[positionY(i) positionY(i+1)]);

    pause(10^-6);

    if i < length(times)
        delete(Mass1);
    end

    i = i + 1;
end
%% End

Nice job. The animations are pretty cool too

Steven Chase - 5 months ago

Yeah, I kept the radii of the circles 0.5 so that I could see them from afar with the particle on the right too. I initially thought the result would be more dramatic, like the particle spiraling off and shooting into infinity.

Krishna Karthik - 4 months, 4 weeks ago

Steven Chase
Jan 10, 2021

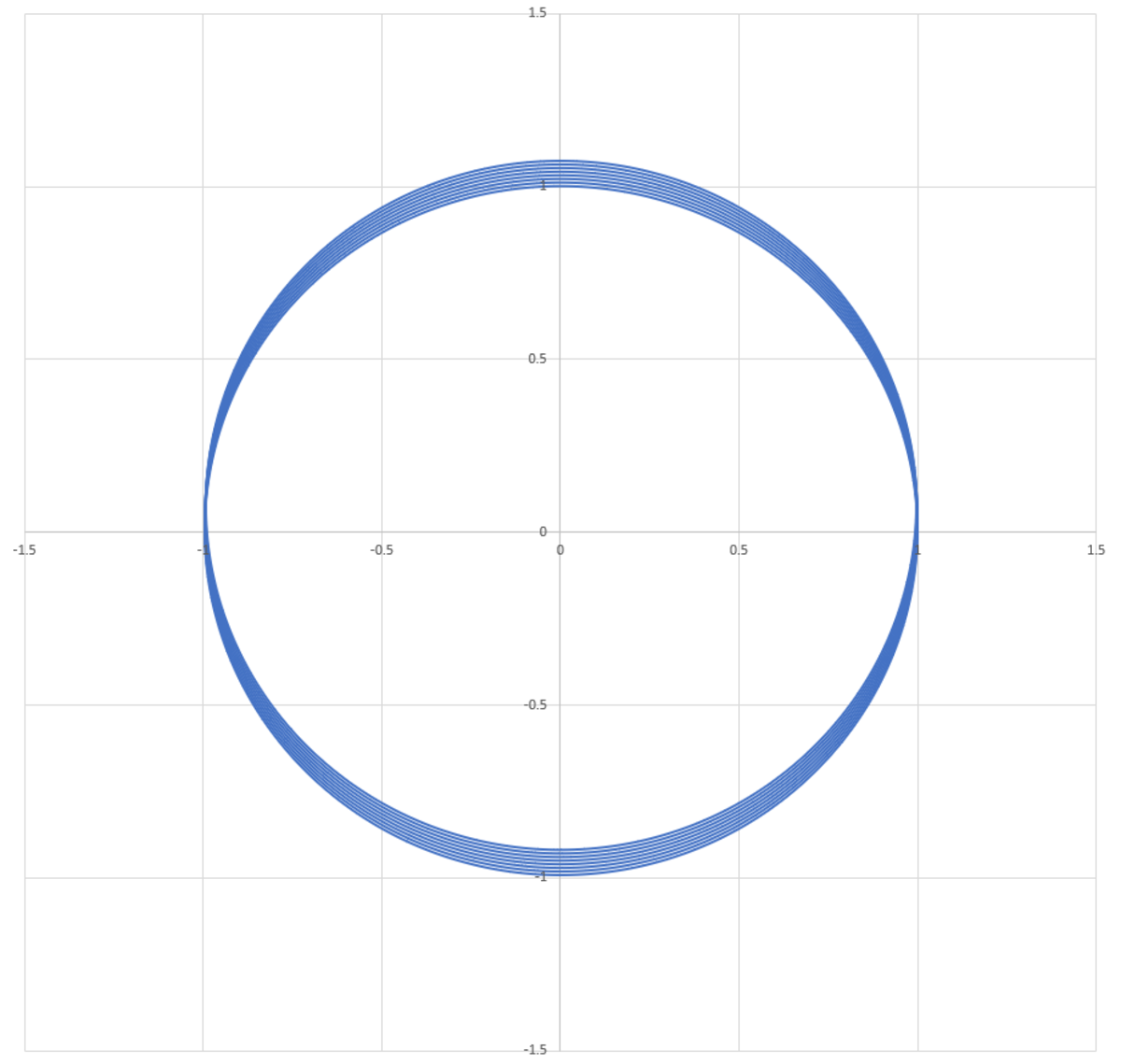
See the solution by @Karan Chatrath for a detailed explanation. Below is a picture of the trajectory with equal scaling on the $x$ and $y$ axes. I solved for the trajectory using Newtonian mechanics and numerical integration, which turned out to be pretty straightforward. The presence of Particle $2$ has a fairly significant effect on the trajectory, even though its force is about three orders of magnitude weaker than that from Particle $1$ . Without Particle $2$ present, the orbit would just be a unit circle centered on the origin.

A Perturbed Orbit

The answer is 0.0732.

3 solutions

0 pending reports