A Plane, A Sphere And A Hyperbola Walked Into A Bar

Substituting for $x+y$ in the second equation, we get $xy=z^2-1/2$ . Hence $xyz=z^3-z/2$ . Now, it is a simple matter of calculus to find global minima of this function.

EDIT : We are doing a constrained minimization here subject to $|z|\leq \sqrt{2/3}$ . Please refer to my reply in response to Calvin's comment.

Suppose we have a cubic with roots $x,y,z$ . Let this cubic be $x^3+ax^2+bx+c$ . Since $x+y+z=0$ , we see that $a=0$ . Thus the cubic can be expressed as $x^3+bx+c$ .

Now, by reverse-Newton's Sums, we see that $x^2+y^2+z^2+2b=0$ ; thus $x^2+y^2+z^2=1=-2b$ and $b=-\dfrac{1}{2}$ . Thus, our cubic has reduced to $x^3-\dfrac{1}{2}x+c=0$ . We want to maximize $c$ in order to minimize $xyz$ .

Drawing a simple graph tells us that the maximum $c$ can be while $x,y,z$ are still real numbers is when two of the roots are equal. Let this multiplicity-2 root be $r$ , and let the remaining root be $R$ . Since $r+r+R=0$ , we see that $R=-2r$ .

Thus $x^3-\dfrac{1}{2}x+c=(x-r)^2(x+2r)$ . Expanding this and matching coefficients gives that $r=\sqrt{\dfrac{1}{6}}$ , and that $c=2r^3$ . Plugging the value of $r$ in and solving for $c$ gives $c=\dfrac{1}{3}\sqrt{\dfrac{1}{6}}\approx \boxed{-0.136}$

I don't think that that's the global minimum.

Here's what I did.

I thought I could use Vieta's formula for a polynomial with degree 3 and solutions $x$ , $y$ and $z$ and dominant coefficient 1.

We know ${S}_{1}=x+y+z, {S}_{2}=xy+xz+yz, {S}_{3}=xyz$ .

We have ${S}_{1}=0$ .

We can get ${S}_{2}$ if we calculate ${(x+y+z)}^2={x}^{2}+{y}^{2}+{z}^{2}+2{S}_{2}$ .

Then ${S}_{2}=-0.5$

So the polynomial is $f(X)={X}^{3}-0.5X-{S}_{3}$ (I used X since x is already used.)

We know that $x$ is a root for $f$ which means that $f(x)=0$ .

Which gives us ${x}^{3}-0.5x-{S}_{3}=0$ .

Then ${S}_{3}={x}^{3}-0.5x$ .

I calculated the derivative of ${S}_{3}$ and got two critic points $\pm \frac { \sqrt { 6 } }{ 6 }$ .

And got a minimum and a maximum, but they're not global.

Let's find a cubic polynomial such that $x, y$ and $z$ are their roots (the idea here is to use the discriminant, $\Delta$ , of a cubic polynomial to force it to have only real solutions). Since, $x+y+z=0$ , it has the following shape: $x^{3}+px+q=0$ $\Delta=q^{2}+\frac{4p^{3}}{27}\leq{0}$ Now, using Newton's Theorem, we have: $S_{2}+p.S_{0}+q.S_{-1}=0$ $1+3p+q.S_{-1}=0...(1)$ Let's find $S_{-1}$ , by using its reciprocal polynomial and Vieta's Formula: $qx^{3}+px^{2}+1=0$ then $S_{-1}=\frac{-p}{q}...(2)$ Substituting $(2)$ in $(1)$ : $1+3p+q.\frac{-p}{q}=0$ $\Rightarrow p=\frac{-1}{2}$ Therefore, this is the polynomial: $x^{3}-\frac{1}{2}x+q=0$ $\Delta=q^{2}+\frac{4\left(\frac{-1}{2}\right)^{3}}{27}\leq0$ $q^{2}\leq\frac{1}{54}$ $\Rightarrow-0.136 \approx -\frac{1}{3\sqrt{6}}\leq{q}\leq \frac{1}{3\sqrt{6}} \approx 0.136$ $q_{min} \approx -0.136$ $min\{xyz\} \approx \boxed{-0.136}$

from given: $xy+yz+zx=-\frac{1}{2}$

we consider a monic cubic polynomial with roots= $x,y,z$

so, from the given,and by vieta's relations, our polynomial $P(a)=a^{3}-\frac{a}{2}-xyz$

now, $P'(a)=3a^{2}-\frac{1}{2}$

easily observable that $P'(a)$ is negative between $(-\frac{1}{\sqrt{6}},\frac{1}{\sqrt{6}})$ and is positive elsewhere

the negative derivative of $P(x)$ signifies it's decreasing nature and the left and right extremities of the set $(-\frac{1}{\sqrt{6}},\frac{1}{\sqrt{6}})$ are the values at which $P(x)$ attains it's local maximum and minimum respectively.

NOW If the polynomial is to have 3 real roots, it should cut the abscissa thrice, thus making the local minimum $≤0$ (or else, the curve wont bulge down into the 4th quadrant in this case)

So, we calculate the local minimum or, $P(\frac{1}{\sqrt{6}})$

which gives the value $-\frac{1}{3\sqrt{6}}-xyz$

By our arguments, this is $≤0$

thus, giving $xyz≥-\frac{1}{3\sqrt{6}}=\boxed{-0.136}$

An alternative method for solving this is to use a Lagrange Multiplier with two constraints. Once the gradients are found, multiplied by some constant (hence the name, "Lagrange Multiplier") and set equal to the gradient of the function to be minimized (i.e. xyz), the problem becomes a system of five equations that can be solved through substitution.

Using the UVW method (http://www.artofproblemsolving.com/Forum/viewtopic.php?t=278791)

$xyz$ is minimized when one of them equals $0$ or two of them are equal.

If one of them is $0$ , $xyz = 0$ .

If two of them are equal, you have $2x + y = 0$ and $2x^2 + y^2 = 1$ . Substituting $y = -2x$ into the second equation gives $6x^2 = 1$ . You want to find the minimum value of $x^2 y$ , which can be rewritten as $\frac{y}{6}$ . When $x$ is positive, $y$ is negative, and vice versa. You want the negative value of $y$ to minimize $\frac{y}{6}$ , so $x = \frac{\sqrt{6}}{6}$ and $y = -\frac{\sqrt{6}}{3}$ so the minimum value of $xyz$ is $\boxed{-\frac{\sqrt{6}}{18} \approx -0.136}$ .

We can solve it by converting the given set of equations into a cubic polynomial. This is what i did.

$First\quad let\quad x,y,z\quad be\quad three\quad real\quad roots\quad of\quad some\quad cubic\quad equation\quad F(t).\\ So\quad the\quad sum\quad of\quad roots\quad will\quad be\quad x+y+z\quad ,\quad and\quad product\quad of\quad roots\quad will\quad be\quad xyz\\ Now\quad applying\quad the\quad identity\quad \\ \Rightarrow \quad (x+y+z)^{ 2 }={ \quad x }^{ 2 }\quad +\quad { y }^{ 2 }\quad +\quad { z }^{ 2 }\quad +\quad 2(xy\quad +\quad yz\quad +zx)\\ we\quad get,\quad (xy\quad +\quad yz\quad +zx)\quad =\quad -0.5\\ So\quad the\quad cubic\quad equation\quad will\quad be\quad { t }^{ 3 }\quad +\quad 0{ t }^{ 2 }\quad -0.5t\quad +\quad d\quad =\quad 0\\ (where\quad d\quad is\quad the\quad constant\quad and\quad is\quad equal\quad to\quad the\quad product\quad of\quad the\quad roots\quad xyz)\\ Solving\quad the\quad above\quad equation\quad by\quad solution\quad of\quad radicals.\\ Put\quad t\quad =\quad p+q\\ \Rightarrow \quad \quad So\quad we\quad get\quad { p }^{ 3\quad }+\quad { q }^{ 3 }\quad +\quad (p+q)(3pq-0.5)\quad +d\quad =\quad 0\\ \quad \qquad Now\quad putting,\quad 3pq-0.5=0\\ we\quad get,\quad p=\quad \frac { 1 }{ 6q } .\quad putting\quad this\quad value\quad in\quad abouve\quad eqn.\quad We\quad get\\ \Rightarrow \quad { q }^{ 6 }\quad +\quad { (d)q }^{ 3 }\quad +\quad \frac { 1 }{ 216 } \quad =\quad 0.\quad Putting\quad { q }^{ 3 }=u\quad so\quad the\quad equation\quad becomes\quad a\quad quadratic\quad in\quad u.\\ { \Rightarrow \quad u }^{ 2 }\quad +\quad du\quad +\quad \frac { 1 }{ 216 } \quad =\quad 0.\quad \\ since\quad x,y,z\quad are\quad real\quad so\quad above\quad quadratic\quad should\quad also\quad have\quad real\quad roots\quad which\quad can\quad only\quad be\quad if\quad { d }^{ 2 }-\sfrac { 4 }{ 216 } \quad \ge \quad 0\\ Or\quad for\quad the\quad minimum\quad value\quad of\quad d,\quad d=\pm \quad \frac { 2 }{ 6^{ 3/2 } }$

This was too easy with my method of logic.

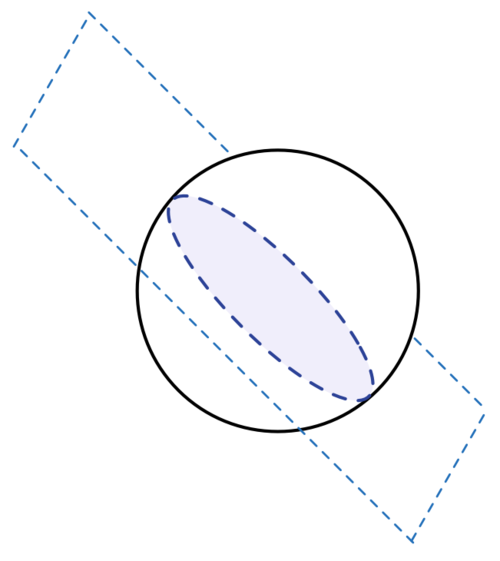
First, imagine/draw out the two functions $x^2 + y^2 + z^2 = 1$ and $x + y + z = 0$ , and look at their intersections, which looks like the picture in the problem description.

Now if you imagine the function $f(x,y,z) = xyz$ , with $f(x,y,z)$ represented as, let's say, the temperature at the spot $(x,y,x)$ , you can tell that the maximum and minimum temperatures will occur along lines that make equal angles with all of the axes. (Think of it like spears of maximum and minimum values jutting straight out of the origin into the octants - 'maximum' spears in the first, third, sixth, and eighth octants, and 'minimum' spears in the second, fourth, fifth, and seventh octants).

Put the original intersection of those two functions into that temperature-graph of $f(x,y,z)$ . It is logical to make the assumption now that the highest and lowest 'temperatures' will occur at the tips of that tilted-circle (the intersection of the two 3d graphs) in the third and fifth octants (the tips of the tilted circle in the second and fourth octants have a $z$ value of zero, so forget those!). The reason for this logic is that those points on the tilted circle of intersection are closest to the lines of maximum values for the function $f(x,y,z)$ .

So, with that assumption, the minimum will occur when $x = y$ :

$x + x + z = 0 \rightarrow x = -\frac{z}{2}$

$x^2 + x^2 + z^2 = 1 \rightarrow \frac{z^2}{2} + z^2 = 1$

$\rightarrow z = \pm \sqrt{\frac{2}{3}}$

We're looking for the minimum value, so

$z = -\sqrt{\frac{2}{3}}$

$xyz = (\frac{1}{\sqrt{6}})(\frac{1}{\sqrt{6}})(-\sqrt{\frac{2}{3}})$

$= \boxed{ -\frac{\sqrt{2} }{6 \sqrt{3}}}$