A plane intersecting two circles

The two points on circle $C_1$ are on the intersection of the two planes with normal vectors $n_1$ and $n_p$ , and also $50$ units away from its center $(50, 25, 0)$ . Therefore:

• $\sin 70° \cos 60° x + \sin 70° \sin 60° y + \cos 70° z = 50 \sin 70° \cos 60° + 25 \sin 70° \sin 60° + 0 \cos 70°$

• $x - 2y + 6z = 0 - 2 \cdot 0 + 6 \cdot 0$

• $(x - 50)^2 + (y - 25)^2 + (z - 0)^2 = 50^2$

which solves numerically to $A(6.1000, 44.5341, 13.8280)$ and $B(93.9000, 5.4659, -13.8280)$ .

Similarly, two points on circle $C_2$ are on the intersection of the two planes with normal vectors $n_2$ and $n_p$ , and also $70$ units away from its center $(25, 50, 0)$ . So:

• $\sin 50° \cos 180° x + \sin 50° \sin 180° y + \cos 50° z = 25 \sin 50° \cos 180° + 50 \sin 50° \sin 180° + 0 \cos 50°$

• $x - 2y + 6z = 0 - 2 \cdot 0 + 6 \cdot 0$

• $(x - 25)^2 + (y - 50)^2 + (z - 0)^2 = 70^2$

which solves numerically to $C(17.2798, -18.9619, -9.2006)$ and $D(48.7831, 109.4220, 28.3436)$ .

By the distance equation, $AB = 100$ , $AC = 68.4620$ , $AD = 79.0126$ , $BC = 80.5530$ , $BD = 120.9167$ , and $CD = 137.4207$ .

$CD$ is the longest, so that is one of the diagonals, which makes $AB$ the other diagonal.

That means the perimeter of the quadrilateral is $AC + AD + BC + BD = 348.9442$ .

And the area of the quadrilateral is the combined areas of $\triangle ACD$ and $\triangle BCD$ , which by Heron's formula calculates to $1833.232 + 4838.2222 = 6671.4542$ .

Therefore, the sum of the perimeter and area is $348.9442 + 6671.4542 = \boxed{7020.4}$ .

Consider:

$\hat{n}_1 = (n_{1x},n_{1y},n_{1z})$ $\hat{n}_2 = (n_{2x},n_{2y},n_{2z})$

The equations of the planes on which each of the circles lies are:

$P_1: \ ((x-50),(y-25),z) \cdot \hat{n}_1 = 0$ $P_2: \ ((x-25),(y-50),z) \cdot \hat{n}_2 = 0$

Having found the equations of these planes, the next step is to find a pair of perpendicular unit vectors on each plane to parameterise the circles. A point that lies of $P_1$ and $P_2$ respectively are:

$R_{P1}=\left(0,0,\frac{50n_{1x}+25n_{1y}}{n_{1z}}\right)$ $R_{P2}=\left(0,0,\frac{25n_{2x}+50n_{2y}}{n_{2z}}\right)$

Therefore: a unit vector on the plane $P_1$ is:

$\hat{n}_{11} = \frac{R_{P1}-R_{C1}}{\lvert R_{P1}-R_{C1} \rvert}$ $\hat{n}_{12} = \hat{n}_1 \times \hat{n}_{11}$

A unit vector on the plane $P_2$ is:

$\hat{n}_{21} = \frac{R_{P2}-R_{C2}}{\lvert R_{P2}-R_{C2} \rvert}$ $\hat{n}_{22} = \hat{n}_2 \times \hat{n}_{21}$

Here $R_{C1}$ and $R_{C2}$ are the position vectors of the circles' centers.

Finally, the parametric equations of each circle are:

$\vec{r}_{C1} = R_{C1} + R_1 \cos{\alpha} \ \hat{n}_{11} + R_1 \sin{\alpha} \ \hat{n}_{12}$ $\vec{r}_{C2} = R_{C2} + R_2 \cos{\beta}\ \hat{n}_{21} + R_2 \sin{\beta} \ \hat{n}_{22}$

This parameterization allows us to 3D plot the circles. The equation of the intersecting plane is given by:

$x - 2y + 6z =0$

The next step to finding the points of intersection of the plane with the circles was carried out numerically. What I did was compute the following quantity:

$D_1 = r_{C1x} - 2r_{C1y} + 6r_{C1z}$ $D_2 = r_{C2x} - 2r_{C2y} + 6r_{C2z}$

Here, $r_{C1x,y,z}$ are the x, y and z components of $\vec{r}_{C1}$ . Similar convention applies to the second circle as well. To see if the point lies on the plane, I swept around both circles iteratively (a programming for loop) and checked if:

$\lvert D_1 \rvert \le \epsilon$ $\lvert D_2 \rvert \le \epsilon$

Where $\epsilon$ is a small number like $10^{-3}$ for instance. The points of intersection are the following:

$P_1 = \left[\begin{matrix} 93.9\\5.4659\\-13.8279\end{matrix}\right]$ $P_2 = \left[\begin{matrix} 6.1\\44.5340\\13.8281\end{matrix}\right]$ $P_3 = \left[\begin{matrix} 17.2798\\-18.9619\\-9.2006\end{matrix}\right]$ $P_4 = \left[\begin{matrix} 48.7831\\109.4223\\28.3436\end{matrix}\right]$

$P_1$ and $P_2$ are points of intersection of $C_1$ and $P_3$ and $P_4$ are points of intersection of $C_2$ .

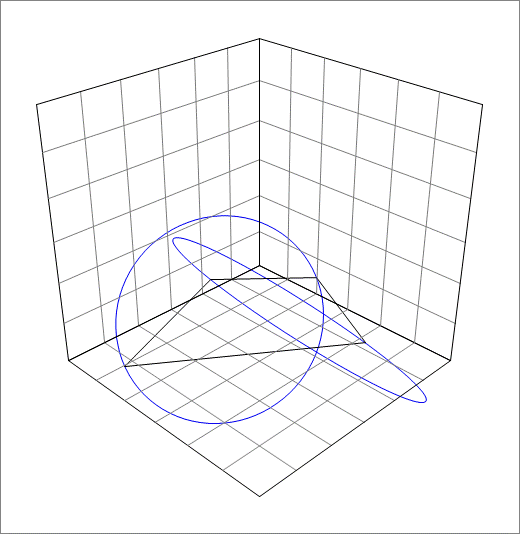
Now, having found these points, it is easy to visualise the geometry. $P_1$ is in red, $P_2$ is in blue, $P_3$ is in green, and $P_4$ is in magenta. The diagram is as follows:

The area of the triangle with $P_1$ , $P_2$ and $P_3$ are:

$\vec{V}_{13} = \vec{P}_1 - \vec{P}_3$ $\vec{V}_{23} = \vec{P}_2 - \vec{P}_3$

$A_{123} = 0.5 \lvert \vec{V}_{13} \times \vec{V}_{23} \rvert$

The area of the triangle with $P_1$ , $P_2$ and $P_4$ are:

$\vec{V}_{14} = \vec{P}_1 - \vec{P}_4$ $\vec{V}_{24} = \vec{P}_2 - \vec{P}_4$

$A_{124} = 0.5 \lvert \vec{V}_{14} \times \vec{V}_{24} \rvert$

The total area of the convex quadrilateral is:

$A = A_{123} + A_{124}$

The perimeter of the quadrilateral is:

$P = \lvert \vec{V}_{14} \rvert + \lvert \vec{V}_{24} \rvert + \lvert \vec{V}_{13} \rvert + \lvert \vec{V}_{23} \rvert$