By Part Takes Forever!

Lazy solution

Because $\sin x < x$ for $x > 0$ $\int_0^\infty \frac{\sin x}{xe^x} < \int_0^\infty \frac{x}{xe^x} = \int_0^\infty e^{-x} = 1.$ Of the four choices given, only $\pi/4$ is less than one.

Relevant wiki: Differentiation Under the Integral Sign

Let $I(a)$ be as follows:

$\begin{aligned} I(a) & = \int_0^\infty \frac {e^{-ax} \sin x}x dx \\ \frac {\partial I(a)}{\partial a} & = \int_0^\infty \frac {\partial}{\partial a} \frac {e^{-ax} \sin x}x dx \\ & = \int_0^\infty \frac {-xe^{-ax} \sin x}x dx \\ & = - \int_0^\infty e^{-ax} \sin x \ dx & \small \color{#3D99F6} \text{See note.} \\ & = \frac {e^{-ax}(a \sin x + \cos x)}{1+a^2} \bigg|_0^\infty \\ & = - \frac 1{1+a^2} \\ \implies I(a) & = - \int \frac 1{1+a^2} da \\ & = - \tan^{-1} a + \color{#3D99F6}{C} & \small \color{#3D99F6}{C \text{ is the constant of integration}} \\ \lim_{a \to \infty} I(a) & = 0 \\ \implies \lim_{a \to \infty} - \tan^{-1} a + C & = 0 \\ - \frac \pi 2 + C & = 0 \\ C & = \frac \pi 2 \\ \implies I(1) & = - \tan^{-1} 1 + \frac \pi 2 \\ & = \boxed{\dfrac \pi 4} \end{aligned}$

---

Note:

$\begin{aligned} J & = - \int_0^\infty e^{-ax} \sin x \ dx & \small \color{#3D99F6} \text{By integration by parts} \\ & = \frac {e^{-ax}\sin x}a \bigg|_0^\infty + \int_0^\infty \frac {e^{-ax}\cos x}a \\ & = \frac {e^{-ax}\sin x}a \bigg|_0^\infty + \frac {e^{-ax}\cos x}{a^2} \bigg|_0 ^\infty + \int_0^\infty \frac {e^{-ax}\sin x}{a^2} \\ & = \frac {e^{-ax}(a\sin x + \cos x)}{a^2} \bigg|_0 ^\infty - \frac J{a^2} \\ \implies a^2J & = e^{-ax}(a\sin x + \cos x) \bigg|_0 ^\infty - J \\ \implies J & = \frac {e^{-ax}(a\sin x + \cos x)}{1+a^2} \bigg|_0 ^\infty \end{aligned}$

Another solution using laplace transform $\int \limits^{\infty }_{0}\frac{\sin \left( t\right) }{te^{t}} dt \\ =\lim \limits_{s\to 0}\int \limits^{\infty }_{0}\frac{e^{-st}e^{-t}\sin \left( t\right) }{t} dt \\ =\lim \limits_{s\to 0}\ell \left( \frac{e^{-t}\sin \left( t\right) }{t} \right) \\ =\lim \limits_{s\to 0}\left( \frac{\pi }{2} -\arctan \left( s+1\right) \right) \\ =\frac{\pi }{2} -\frac{\pi }{4} =\boxed{\frac{\pi }{4}}$

Relevant; Leibniz Formula for $\pi$

By Taylor expansion we know that

$\begin{aligned} \sin x= \sum_{n=0}^\infty \frac{(-1)^n x^{2n+1} }{(2n+1)!}=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots \end{aligned}$

which implies

$\begin{aligned} \int_0^{\infty} e^{-x} \frac{\sin x}{x} &= \int_0^{\infty} \sum_{n=0}^\infty e^{-x} \frac{(-1)^n x^{2n}}{(2n+1)!} \end{aligned}$

It is easy to see (using integration by parts and induction) that for $m \in \mathbb{N}$

$\begin{aligned} \int_0^\infty e^{-x} x^m=m! \end{aligned}$

Given that the series converges (by the ratio test) to an integrable limit we can change the order of integration using Fubini's Theorem

$\begin{aligned} \int_0^{\infty} \sum_{n=0}^\infty e^{-x} \frac{(-1)^n x^{2n}}{(2n+1)!} &= \sum_{n=0}^\infty \int_0^{\infty} e^{-x} \frac{(-1)^n x^{2n}}{(2n+1)!}\\ &= \int_0^{\infty} e^{-x} (1-\frac{x^2}{3!}+\frac{x^4}{5!}-\dots\\ &=1-\frac{1}{3}+\frac{1}{5}-\dots =\frac{\pi}{4}, \end{aligned}$

Where the last equality holds by the Leibniz formula for $\pi$ .

consider I(a)= $\frac{sin(ax)}{xe^x}$ now integral of this withrespect to dx will be a fn of "a" partial differentiatin wrt "a" I'(a) =

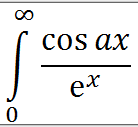
now apply by parts.. and then get I(a) a=1 at last

This solution uses methods of complex analysis related to Cauchy's Residue Theorem. In particular, we make use of Cauchy's Theorem.

Let $I=\int_0^\infty \frac{\sin x}{x e^x}dx$ . Then let $f_+(z)=\frac{1}{z}e^{(i-1)z}$ and $f_-(z)=\frac{1}{z}e^{(-i-1)z}$ .

Observe that $I=\mathcal{Im}(\int_0^\infty f_+ (z)dz)=-\mathcal{Im}(\int_0^\infty f_- (z)dz)$ .

Consider for $\epsilon, R>0$ , $\gamma$ the contour in the complex plane consisting of:

• $\gamma_\epsilon$ , a quarter arc of radius $\epsilon$ , centred at zero,

• $\gamma_R$ , a quarter arc of radius $R$ , centred at zero,

• and the real and imaginary line segments connecting them,

the whole contour in positive orientation.

Then it follows that: $\int_{\gamma_R} f_+ (z)dz+\int_{\gamma_\epsilon} f_+ (z)dz+\int_\epsilon^R f_+ (z) dz+\int_{iR}^{i\epsilon} f_+ (z) dz = \int_{\gamma} f_+ (z)dz$ .

But $\int_{\gamma} f_+ (z)dz = 0$ as $f_+$ is holomorphic on $\gamma$ , and $\mathcal{Im}(\int_\epsilon^R f_+ (z) dz)=\mathcal{Im}(\int_{iR}^{i\epsilon} f_+ (z) dz)=I$ as $\epsilon\to 0, R\to \infty$ , which we can see by applying the substitution $z=ix$ to the second integral.

Hence we have $\mathcal{Im}(\int_{\gamma_R} f_+ (z)dz)+\mathcal{Im}(\int_{\gamma_\epsilon} f_+dz) +2I=0$ (as $\epsilon\to 0, R\to \infty$ )

It remains to find $\lim_{R\to\infty} \int_{\gamma_R} f_+ (z)dz$ and $\lim_{\epsilon\to 0} \int_{\gamma_\epsilon} f_+ (z)dz$ .

Indeed we have $||\int_{\gamma_R} f_+ (z)dz||\leq \frac{\pi}{2} R ||f_+ || \leq \frac{\pi}{2e^R}$ as $||e^{iz}||$ is bounded above by one on the upper half plane. Hence as $R\to\infty$ , $\int_{\gamma_R} f_+ (z)dz\to 0$ .

Now we apply the substitution $z=\epsilon e^{it}:0\leq t < \frac{\pi}{2}$ to get $\int_{\gamma_\epsilon} f_+ (z)dz=\int_{\frac{\pi}{2}}^0 \frac{1}{\epsilon e^{it}} e^{\epsilon (i-1)e^{it}}\times \epsilon i e^{it}dt=-i\int_0^{\frac{\pi}{2}} e^{\epsilon (i-1)e^{it}} dt (*)$ .

Taking $\epsilon \to 0$ we get $(*)\to -i\int_0^{\frac{\pi}{2}} dt=-i\frac{\pi}{2}$ .

Putting it all together: $\mathcal{Im}(0) + \mathcal{Im}(-i\frac{\pi}{2}) + 2I = 0\implies I=\boxed{\frac{\pi}{4}}$

Max value of the function is 1 and it is decreasing so area must be <1 opt D

Just use diff under imtegral sign by replacing sinx by sin ax