A geometry problem by Ajay Sambhriya

Geometry Level 3

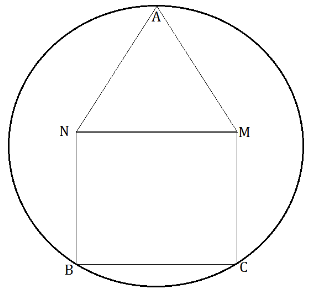
A pentagon BNAMC is inscribed inside a circle such that AMN is an equilateral triangle and BNMC is a square of side length 4.

Find the radius of the circle.

The answer is 4.

2 solutions

Marta Reece
Mar 19, 2017

A bit less clever: Define $x=OD$ where $O$ is the center of the circle.

Get two expressions for the radius.

From the equilateral triangle on top $R=AO=\frac{\sqrt{3}}{2}\times 4+x=2\sqrt{3}+x$ .

From the right triangle $OEC$ as $R=\sqrt{(4-x)^2+2^2}$ .

Resulting equation: $2\sqrt{3}+x=\sqrt{(4-x)^2+4}$ has a solution $x=4-2\sqrt{3}$

So the radius is $R=2\sqrt{3}+4-2\sqrt{3}=4.$

Ajay Sambhriya
Mar 15, 2017

I am not sure that the word "inscribed" is the best way to describe relationship between the pentagon and the circle. It is actually only the triangle $ABC$ that is inscribed in a sense of all of its vertices being on the circle. Or am I wrong there?

Marta Reece - 4 years, 2 months ago

i believe what you are saying is correct .thanks for pointing it out .

Ajay Sambhriya - 4 years, 2 months ago

Why have you written : BOC = 2BAC = 60 and $AB$ = $OC$ that should be $OB$ = $OC$ so BOC is equil. Even when $AB$ is not equal to $OC$ , the later will always be true.

Rafmac Tihor - 4 years, 2 months ago

This is not my solution, but I can see how $\angle BOC=2\times\angle BAC$ . I think your problem is with the following statement. It's probably a typo and it should have read $AO=OC$ .

Marta Reece - 4 years, 2 months ago

Yep, That's what I actually meant.

Rafmac Tihor - 4 years, 2 months ago

@Rafmac Tihor – Can you fix it?

Marta Reece - 4 years, 2 months ago

A geometry problem by Ajay Sambhriya

The answer is 4.

2 solutions

0 pending reports