Russian Nesting Squares?
The diagram consists of three nested squares. The lengths of the line segments are A B = 4 , B C = 3 , and C D = 2 .
What is the area of the smallest square?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Very clean and concise solution!
I'm sorry but with what logic do we have AX =2
Log in to reply
Glad you brought this up. This comes up in the proofs for Pythagorean Theorem . ∠ D X C = θ , and so the angles at X are θ , 9 0 and 9 0 − θ . So the triangle on the right has angles 9 0 − θ , 9 0 and θ , which makes it similar to the one on the left. Since they share a hypotenuse (the light blue square length), they are similar, so we can say that A X = 2 .
Log in to reply
how is cx =3
@ Brilliant - This should have been placed in the "Intermediate" category instead. Also, it is so not drawn to scale that it is distracting.
I got the same result using Pitagoras, but I don't understand why I can't use the theorem of proportional triangles in this case... what I am overlooking?
Log in to reply
I think you may be assuming that all triangles are orientated by the same amount? Use trig on the diagram, not all triangles have the same angles and thus are not all similar.
Sender is wrong. Square root of 13 multiplied by square root of 13 is roughly equal to 7.211
Log in to reply
square root of 13= (13)^(1/2); We know that, (13)^(1/2) x (13)^(1/2) =(13)^(2/2)=13
Using the pythagorean theorem , we know that the second square has a side of 5 . Since 2 + the other segment equals 5, the segment that forms a right triangle with the line segment of length to equals three. Doing Pythagorean for the third square yields the side as the square root of 13 because 4 + 9 = 13. The area of the square is 1 3 .
Thanks for the answer
What was the question???
Its weird I knew that smaller segment in AC is 2 but I can't explain why I did, could you explain that bit?
Log in to reply
All the triangles formed by the light blue square inside the green square have to be congruent. This would mean that you can conclude that the smaller segment is 2. Here's how you can know those triangles are congruent:
The light blue square's side length is 5 on all sides, this is a congruent side on all of the triangles. If I can find two pairs of corresponding angles that are also congruent, that would make the triangles congruent. Of course, there's the right angle. The other pair of angles is trickier. Notice that the two acute angles inside a right triangle always add up to 90 degrees (Thus the smaller two angles inside each of the triangles in the corner add up to 90 degrees). Also notice that at the corner of the light blue square, the two acute angles have to add up to 90 degrees also since the three angles there add to 180 degrees, and the right triangle of the square takes up 90 degrees. This means that the smaller angle adds to 90 with (a) the larger angle inside the same triangle as itself, and (b) the larger angle inside the triangle in the next corner. This means the two larger acute angles have to be congruent, since two angles that are complementary with the same angle have to be congruent. So, the triangles are congruent by AAS congruence.
Using only area: area of green square is area of blue square minus 4ABC, means 25 (means AC=5, means CX=3) . Area of smallest square is area of green sguare minus 4CXD, means 13.
Nice and different approach! I like this solution :)
This method of Anca Marian is the most simple and elegant solution. Also, it is deeper (mathematically speaking) as it prompts the following questions: (1) What is the next smaller nested square ? (2) What is the general formula to generate a next square ? (3) What is the limit of the sum of successive nested squares ? (4) Can any regular (equal-sided) polygon be nested and a formula derived ? A. Ferguson
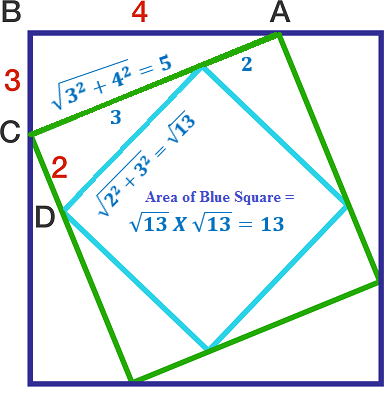
By Pythagoras , A C 2 = 3 2 + 4 2 ⟹ A C = 5 .
By symmetry, A X = 2 ⟹ X C = A C − A X = 5 − 2 = 3 .
Second use of Pythagoras tells us that the blue length squared (i.e. the area of the smallest square) = 2 2 + 3 2 = 1 3 .