Plus Minus Times Divide Zero Through Six
( 4 + 5 − 3 × 6 ÷ 2 ) 0 + 1 = ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
20 solutions
But isn't anything raised to the power zero 1 ??
Log in to reply
Yes. By convention, mathematicians have also defined 0 0 to equal 1.
Log in to reply
Yes, you are right. Many universities define 0 to the power of 0 as 1.
Log in to reply
@William Park – "The debate over the definition of 00 has been going on at least since the early 19th century. At that time, most mathematicians agreed that 00 = 1, until in 1821 Cauchy[20] listed 00 along with expressions like 0 / 0 in a table of indeterminate forms. In the 1830s Libri[21][22] published an unconvincing argument for 00 = 1, and Möbius[23] sided with him, erroneously claiming that \scriptstyle \lim {t \to 0^+} f(t)^{g(t)} \;=\; 1 whenever \scriptstyle \lim {t \to 0^+} f(t) \;=\; \lim_{t \to 0^+} g(t) \;=\; 0. A commentator who signed his name simply as "S" provided the counterexample of \scriptstyle (e^{-1/t})^t, and this quieted the debate for some time. More historical details can be found in Knuth (1992).[24]
More recent authors interpret the situation above in different ways: Some argue that the best value for 00 depends on context, and hence that defining it once and for all is problematic.[25] According to Benson (1999), "The choice whether to define 00 is based on convenience, not on correctness."[26] Others argue that 00 should be defined as 1. Knuth (1992) contends strongly that 00 "has to be 1", drawing a distinction between the value 00, which should equal 1 as advocated by Libri, and the limiting form 00 (an abbreviation for a limit of \scriptstyle f(x)^{g(x)} where \scriptstyle f(x), g(x) \to 0), which is necessarily an indeterminate form as listed by Cauchy: "Both Cauchy and Libri were right, but Libri and his defenders did not understand why truth was on their side."[24]
Treatment on computers[edit]Write a comment or ask a question...
Log in to reply
@Yuliya Skripchenko – I don't understand. I thought that numbers to the power of 0 cancel out.
x^0 = 1(x^0)
Since x^0 cancel out, 1(x^0) would cancel to 1.
Same would go to 0, right?
@William Park – But I read in a lot of books that 0 to power of 0 is undefined and every number except zero to the power of 0 is as 1 .
Log in to reply
@Juliet Hanson – Check out the links provided by Llewellyn Sterling. In a very small number of cases, like functions, that can be debatable. But for most circumstances, it's 1.
@Juliet Hanson – Yeah, when you talk about limits of function at a certain point, a function that simplifies to 0^0 is considered indeterminate form.
Log in to reply
@Faith Patrick – It is in an indeterminate form, but you can use several methods to get it to a non-indeterminate form. Despite any real criticism it becomes (0^0) = 1.
@William Park – Think about it. Anything to the zeroth power is 1, but 0 to any power is zero. The reason it is undefined is because it combines those things and could be 0 or 1.
@William Park – Anything to the zeroth power is one, but 0 to any power is zero. A question is indeterminable if they combine the two.
@William Park – Of course. High school classes always say that it is undefined.
Log in to reply
@Lew Sterling Jr – In high school and again in college, the instructors said "anything to the power of zero is one." The college professor even claimed that a house to the power of zero equals one.
n 0 = 1 only if n = 0 . In that case, 0 0 is indeterminate. Demonstration: 0 0 = 0 1 − 1 = 0 1 / 0 1 and you get 0/0 that is indeterminate, because if n = 0 / 0 then n ∗ 0 = 0 and it's true for every number. When you say it equals 1, you're not totally wrong: 0/0 is ALSO 1, but also 2, 3, -86, π, √2, etc
Log in to reply
@Simone Peroni – A counterargument to that was already provided by someone else. Consider applying the same reasoning for 0 2 . You can also write it as 0 2 = 0 1 0 3 = 0 0 But that means that 0 2 can also be anything, which is false since we know it's specifically 0 .
@Simone Peroni – a = 0 and m > n > 0 ⇒ a m − n = a n a m .
a = 0 and m ≥ n > 0 ⇒ a m − n = 0 m − n and m − n ≥ 0 .
a = 0 and m ≥ n > 0 ⇒ a n a m is undefined.
What you've really proved was that a n a m is undefined when a = 0 and m ≥ n > 0 . There's no question to that. However, a m − n = a n a m when a = 0 and m > n > 0 .
Log in to reply
@André Cabatingan – I don’t understand this. a = 0 and m≥n>0 ⇒ a^(m-n) is undefined (but the expression a^m/a^n is valid, even though its value is undefined). However, when a = 0 and m>n>0, a^(m-n) ≠ a^m/a^n. Both cases seem the same, since they both have zero in the denominator. Why is the equality between m and n so important in the first inequality?
@Simone Peroni – Yep, I agree with you
Exactly every number with exponential zero is one
Yeah. I always thought x^0 was 1, regardless of the value of x. So shouldn't that make the answer 1+1 = 2?
I'll agree with you if you demonstrate that 0 0 = 1 . It's known that for a = 0 : a 0 = a n − n = a n a n = 1 But you can't apply the same to a = 0 , because you would get 0/0 that is indeterminate
Log in to reply
@Simone Peroni – I was pointing out that your demonstration was illogical. Idk if you saw that.
Log in to reply
@Osama Kawish – I got it, I have figured out it. But I asked you another thing, didn't I? You have said that 0 0 is 1, so demonstrate it
Log in to reply
@Simone Peroni – Oh. For that, refer to Llewellyn Sterling's links. The overall reason is a little detailed.
Agreed. Asking people question on topics where there is professional debate is like asking who your favorite football team. Not nice!
I agree with you
no 0^0 is =1 in the limit so technically 2 is a correct answer
Log in to reply
0^0 is 1 in the limit?! I can easily give you a limit which is non-equal to 1: lim x ↓ 0 0 x = 0 Or lim x ↓ 0 ( x ) ln x 1
I use ↓ to indicate a limit taken for x approaching 0 downwards, i.e. starting from positive numbers. The limits above are indeterminate if you don't take them downwards.
Anything except 0. By convention 0 raised to anything is 0 but then anything raised to 0 is 1, thus mathematicians have defined 0 to the power of 0 to be indeterminate
Log in to reply
Incorrect. 0 to any nonzero power is zero, but any value to the zero power is 1. Go study binary relationships and you will understand. The correct answer is 2, period.
Ah. Thanks.
That's probably right. anything power 0 is 1 even if it is 0 ^0 too i guess
OK. I thought the reason to anything raised to the power zero equals 1 as the following. (a^3)/a = a^2, (a^2)/a = a, a/a = a^0 = 1, But in this case a = 0. 0/0 is indeterminate. So a^0 should be indeterminate. Am I right?
you are right. anything raised to the power o is one. any thing divided by zero is infiniy. So this answer should be 2
That's what I thought too. I hate these trick questions.
Anything to Power 0 is 1.
It should be 2, not indeterminate
I'm reporting this question. Look right here and right here .
Log in to reply
Euler's convention does not change the fact that 0 0 = 1 ⇒ 0 0 = 1 the result of which is false in most cases. Mathematicians understood this in the 18th and 19th century debates, but mostly settled on 0 0 = 1 anyway since it makes some theorems easier to deal with at 0 . That does not mean that 0 0 is purely 1 , especially for arithmetical purposes.
Log in to reply
How does 0 0 = 1 imply 0 0 = 1 The exponent of 0 has little to do with fractions. That fraction in exponent form is actually 0 0 = 0 ⋅ 0 − 1 which is not that same as 0 0 . I could be missing something.
Log in to reply
@Osama Kawish – 0 0 = 0 1 0 1 = 0 0
Log in to reply
@Caleb Townsend – You can't do that. Otherwise, 0 2 = 0 1 0 3 = 0 0
even though 0 2 is obviously 0
Log in to reply
@Siddhartha Srivastava – Actually.. According to the rules of exponents, what Caleb did does work.
Log in to reply
@Billy Zottnick – Even if the rules lead to an obvious contradiction? The rules for exponents are usually defined for a non zero base.
@Billy Zottnick – Caleb is incorrect because those rules only apply to nonzero exponents.
@Caleb Townsend – x n x m = x m − n is true only ∀ x = 0 .
@Caleb Townsend – Did you see this link I provided several hours ago? Look at the picture up top.
Sensible. When I said Euler's number earlier, I meant that Osama spelled my name without an extra "e". He said "Llewllyn" instead of "Llew e llyn", but I did see he changed it. :)
Log in to reply
@Lew Sterling Jr – Ah I was referring to that Euler advocated the convention 0 0 = 1 .
Log in to reply
@Caleb Townsend – True. Euler did do that. to make it 1. However, I just think it is wrong that many places teach us the wrong way in calculus.
no ,they are totally different things you are talking about here ,0^0 exist and is exactly equals to 1 in the limit whereas 0/0 can be anything from L'Hopital's rule
0/0 is not equal to 1 as anything divided by 0 is infinite.
Log in to reply
@Hari Krishnan – Zero to the 50th power (or even to an infinite power) is still zero, so zero divided by zero is not infinity.
We can evaluate 0 0 by considering the limit of x x as x → 0 , which is 1. Hence it is not of any indeterminate form, and the answer should be 2.
Log in to reply
This is not entirely true, it depends on if you take the limit from the natural side (x = 4, x = 3, x = 2) or the imaginary side ( x = 4i, x = 3i, x = 2i) one goes to 1, the other to 0.
I first answered this knowing 0^0=1. After getting the question wrong i checked my answer by using the "scratchpad" provided in this . If you type in "0^0" the answer comes up as 1.
When applied to your question the answer is 2. Would you please either change the answer or inform the program administrators they have a glitch in the "scratchpad". -_-
Following my common sense I put 2. I used PEMDAS, but I not solved the parenthesis equation, I immediate solved as 1! LOL
So the answer is indeterminate or 2 - -. Too much debate - -
As said by mathematicians 0^0 is 1. Then how it can be indeterminate. And also the google' answer is also 1. Then how it can be indeterminate.
If you google 0^0 , the Google calculator shows 1
power zero is equal to 1 +1 =2
what if i take the expression [(4+5-3 6/2)^1/(4+5-3 6/2)] +1. therefore the the expression would take to 1or indeterminantant if solved , but by limits , it offers a solution of 1 which when added to1 results in 2
I don't see why are people arguing about the expression's value being 2. Here's direct quotation of Michael Mendrin's comment on this topic (pulled from this thread) -
"Indeterminate" means that there exists more than one alternative evaluation of the expression, which is clearly the case here. Hence, it's indeterminate. Given any value x , some argument can be made that 0 0 = x . So, people can choose one value of x as a "convention", but that's all it is, a convention, and not a derived mathematical fact.
Mathematics does not say that every expression necessarily evaluates to an unique value.
Using order of operations (PEMDAS), the equation in the parenthesis simplifies first to (4+5-9÷2) then (4+5-4.5) (9-4.5) so the solution is (4.5)^0+1...1+1=2
Log in to reply
Nope. (4+5-3x6÷2) = (4+5-9÷2)
(4+5-3x6÷2) = (4+5-18÷2) = (4+5-9) = 0
Otherwise nobody would be arguing about the value of 0 0 .
Exactly, the school of thought is zero power zero is undetermined.
Log in to reply
Graph x^x (desmos.com is the best for me to use) and tell me what y-value you get when x= 0.
Log in to reply
it goes to 1, that's true, but if you consider 0 0 as 0 1 − 1 or 0 1 0 1 you'll get a division by zero, that is the indetermination
Log in to reply
@André Winston – x n x m = x m − n is true only ∀ x = 0 .
@André Winston – True, but based on limits, graphing, and notations,they still are saying that it 1 and not indeterminate.
@André Winston – If we will use that line of reasoning, though, 0 1 would also not be determined, because you could consider it as 0 2 − 1 or 0 1 0 2 , where you'll also get a division by zero.
Don't you think 0 2 − 1 = 0 1 = 0 1 0 2 ?
0^0 is one of the 7 indeterminate forms
Log in to reply
List all 7 of the indeterminate forms, please.
Here's a reasonable link for this issue:
http://www.askamathematician.com/2010/12/q-what-does-00-zero-raised-to-the-zeroth-power-equal-why-do-mathematicians-and-high-school-teachers-disagree/
Well.. I learned that 0 at power 0 equal 1. So if the answer in the () is to power 0, the answer of the equation should be 2 because everything power 0 equal 1, so 1+1=2 right? I'm in secondary 5, I didn't learned a lot in maths...
Log in to reply
Now this guy has been taught right. Good job, man.
Ah, one more thing ... What if x = 0?
Positive exponent (n> 0) 0^n = 0 Negative exponent (n <0) not defined! (Because we divide by 0) Exponent = 0 Ummm ... read below! The Strange Case of 0^0
There are two different arguments about the correct value. 0^0 could be 1, or maybe 0, so some people say it is "undetermined" x^0 = 1, so ... 0^0 = 1 0^n = 0, so ... 0^0 = 0 When in doubt ... 00 = "indeterminate"
Log in to reply
1 is the multiplicative identity of real numbers.
If n > 0, then 0^n = 0, because you multiply 1 n times by 0.
n^0 is as simple as not multiplying 1 by n. Thus n^0 = 1 for any real number n.
Log in to reply
But if you multiply any numbers with zero, the results always zero. So 1 as an identity of real numbers doesn't really work there
genius i thought the ans would be 2 .
but the equation is raised to the power of zero , i thought anything raised t o zero wouod equal zero, and then just do 0+1
Log in to reply
Nope. By the way, ask your current math teachers what do they say 0^0 is. something tells me that all of the math teachers you ask me will be saying "undefined".
Zero power of anytnings is equal to 1, so right ans is 2.
)X^0 = 1?)
in response to Caleb Townsend 0^0 is 1. And google' answer is also 1. then how it can be indeterminate. Link is here from which i got 0 ^0 is 1https://www.google.co.in/search?q=what+is+0%5E0&oq=what+is+0%5E0&aqs=chrome..69i57j0.11607j0j1&sourceid=chrome&ie=UTF-8
Umm...PEMDAS...
Ur answer correct but failed to explain in bodmas rule
any finite number raised to the power zero is one and zero is a finite number.
Log in to reply
The reason any non zero number raised to the 0 is because you are dividing that number by itself. 1^0 is 1 because it is 1/1. 2^0=2/2 and so on. 0^0=0/0 which is indeterminate by nature.
but shouldn't it be approaching zero to the power approaching zero indeterminate form? exact zero to the power exact zero is 1.
anything raised to the zero is 1. I believe the only time it is undefined is when you are raising infinity to the zero
Exactly. 0^0 is indeterminate.
(X^a)/(X^a)= X^(a-a)= X^0= 1 If a=0,.......
There is no practical application of this, it's completely theoretical so in real life it makes no difference because it will never happen. Unless it's how you open a worm hole, in that case that's awesome.
but as per google it is 1. For 0^0
0^0 = 1 guys if you don't trust me check google = 1 and 1+1 = 2 not indeterminate. This problem is wrong, don't worry if you were marked wrong
Log in to reply
Come on guys. We're having a mathematical discussion here. Don't bring Google into it. You should be bringing mathematical papers and thesis as well as your own logic and understanding. Google is irrelevant.
Log in to reply
guess what: Google also has mathematical papers and theses as well.
this question is wrong as we dont follow the bodmas rule.
The gamma function, the fundamental mathematical function which defines factorials, can be used to show 0^0=1. In most math classes, its treated as undefined, but i was a physics grad student and have had to use the gamma function in statistical mechanics, along with the equalities 0!=1 and 0^0=1. Look it up on the computational search engine wolfram alpha.
I've learned in class that any number raised to 0 is equal to 1. Thus, the answer is 2.
Okay leaving the fact [ 0^0 = ? ] Consider this approach.
we know: (a+b)^n = nC0×a^n×b^(n-n) + nC1×a^(n-1)×b^(n-n+1) + ..... + nCn×a^(n-n)×b^n.
so,
(4+5-3×6÷2)^0 + 1 = [(9 - 9)^0 ] + 1 = [ 0C0×9^0×(-9)^0 ] + 1 = [ 1×1×1 ] + 1 = 1 + 1 = 2
agree ?
I think this should be 2
anything raise to power 0 is 1
what no the right is anything^0=1 and 1+1=2 you solution is incorrect
I have used set theory to prove that 0^0=1.
En nuestra época de colegio nos dicen que todo número elevado a cero vale uno, y también nos dicen que cero elevado a cualquier número vale cero, es decir: a^0=1 \ 0^b=0 Pero siguiendo estas dos afirmaciones nos encontramos con un problema: ¿Cuánto vale 0^0? Según la primera de las afirmaciones valdría 1, pero según la segunda valdría 0. ¿Con cuál nos quedamos?. Muchos diríais: 0^0 es indeterminación. Sí pero no. No, porque el caso que nos ocupa no es el de una función (sucesión) que tiende a 0 elevada a otra función (sucesión) que tiende también a 0. Es decir, no queremos calcular el límite de cualquier función que dé una indeterminación 0^0, sino que queremos saber cuál es el valor del número 0^0 (recalco esto porque es muy importante y suele llevar a errores: no es lo mismo un número que una función cuyo límite es ese número). ¿Cuál es la forma más coherente matemáticamente hablando para dar un valor a 0^0?. Pues a través de un límite. Sí, cierto, en el párrafo anterior he dicho que no estamos calculando cualquier límite que dé como indeterminación 0^0, pero no es eso lo que vamos a hacer. Vamos a utilizar una función concreta para encontrar ese valor. ¿Cuál?. Pues la más lógica: x^x. Vamos a calcular su límite cuando x tiende a 0. Lo haremos por el procedimiento normal: llamar A al límite y aplicar logaritmo a ambos lados de la igualdad. Utilizando después la regla de L’Hopital llegamos a la solución:
lim {x->0} x^x=0^0=A log{A}=lim {x->0} log{x^x}= Propiedad de los logaritmo =lim {x->0} x * log{x}=''0 * (- infty) Tenemos otra indeterminación. Para resolverla pasamos x como 1 / x al denominador y aplicamos la regla de L’Hopital en el paso *: log{A}=lim {x->0} log{x} / (1 / x) = * =lim {x->0} (1 / x) / (-1 / x^2) = Operamos = lim {x->0} (-x)=0 Tenemos entonces que log{A}=0. Por tanto A=1 Es decir, el valor más coherente matemáticamente hablando (y por tanto el que se utiliza en los casos en los que es necesario) es: 0^0=1
I learned 0^0 =1 (and get the same result with Google) but apparently there is different meanings and as long that discussion is not settled questions involving 0^0 should not be here on brilliant.org because some will fail due to different learnings.
http://www.askamathematician.com/2010/12/q-what-does-00-zero-raised-to-the-zeroth-power-equal-why-do-mathematicians-and-high-school-teachers-disagree/
But don't we apply BODMAS? I mean won't it be ((((4÷2)×6)+5)-3) = 14
Set Theoretically, 0^0 can be proven to be 1
this is kind of sad that people dont realize its indeterminate because 0^x=0 but x^0=1 giving 2 values so booom
@Lew Sterling Jr Please don't be a sore loser because you wrote those two posts. Really, it's just one problem.
anything to it's power tending to zero will only give an indeterminant form. Here's nothing like so. therefore o^o here will be ZERO!!!
You are very correct it is indeterminate, as 0^0 is indeterminate form and adding it to 1 will provide an indeterminate solution.
Seriously, I said 2 because my brain was thinking "oh, it's raised to the power of zero so it's 1."
This my way of thinking about exponents, 3^3 is just 1 x three 3's and 7^0 is just 1 x zero 7's or just 1 so 0^0 would be 1 x zero 0's, So where is the error in that reasoning?
When the power raised to zero is tending to zero then only it is an in-determinant.However here the power is absolute zero . Therefore 0^0 will be zero & 0^0(tending to) will be an in-determinant.
0^0 is not an indeterminate form . it would have been indeterminate if the numbers in position of 0& 0 were tending to 0 .In this case the answer should be 2 .
Log in to reply
You are incorrect. 0^0=0/0. 0/0 is indeterminate.
I guessed the answer even before evaluating the expression
Distributive property shows that (4+5-3 X 6 / 2)^0 is equal to 4^0+5^0-3^0 X 6^0 / 2^0 which the becomes 1+1-1 X 1 / 1 which equals 1 thus the final answer should be 2
0^0 equals 1, so 1 plus 1 is 2.....
But sir 9-3×3 then 9-3=6×3=18 . ...
Log in to reply
PEMDAS: Parentheses, Exponents, Multiplication, Division, Addition, Subtraction
Has to be in that order.
Also, if it was 18, then 18^0 = 1
Then: 1 + 1 = 2 (still)
Use BODMAS rule then ul get 0^0+1
hey bhuwan dont forget the basics "BODMAS"
Log in to reply
Ha. Not a math wizard here.. but why wouldn't 0^0 be 0...
It goes in order from left to right for order of operations, so it would be 3x6=9 then 9÷3 for 4.5.
Log in to reply
Division and multiplication order is irrelevant. 2*4/8=1 regardless of the order.
Another controversy: Is 0 0 indeterminate or is it undefined? One would wish, for the sake of clarity, that the term "undefined" would be reserved for numbers, while "indeterminate (form)" refers to limits.
I think it is better to say undefined
problem is that exponential functions related to growth or decay of some thing.... so logicly at a point o something exist and it's in one unit
I agree, should be 1
But it has been defined.. as 1.
Log in to reply
Asking what 0 0 is is just like askin' 0 0 = x which also same for 0 x = 0 which is all numbers.But in this question there only one true answer.So 0 0 is undefined
Just because something is raised to the zero power does not guarantee 1 always. 0^0 is an exception.
Evaluating inside the parenthesis gives 9-9 which is 0. This, 0^0 is found. Since this expression is indeterminate it follows that the entire expression is indeterminate.
If any of the numbers inside the parentheses were obtained from a real-valued measurement, then (...)^0 should be taken to be 1. Blanket statements about 0^0 being "undefined" are misleading, because in several mathematical contexts 0^0 is defined as 1 in order to make important formulas (such as binomial expansion) work out without exception. I suggest that this quiz question be removed.
0^0 = 0^(1-1) = (0^1)/(0^1)
Division by zero
( 4 + 5 − 3 × 6 ÷ 2 ) 0 + 1 ( 4 + 5 − 9 ) 0 + 1 0 0 + 1
What's a number raised to 0 equal to?
~~~~~~~~~~~~~~~~~~~~
If the number is greater than 0 , such as 2 ,
2 0 × 2 1 × 2 2 = 2 0 + 1 + 2 2 0 × 2 × 4 = 2 3 2 0 × 8 = 8 2 0 = 8 ÷ 8 2 0 = 1
~~~~~~~~~~~~~~~~~~~~
If the number is 0 ,
0 0 × 0 1 × 0 2 = 0 0 + 1 + 2 0 0 × 0 × 0 = 0 3 0 0 × 0 = 0
0 0 can be any number—hence, an indeterminate form .
0^0 is 1 anything raised to 0 is 1
pemdas rule (4+5-(3*6)/2)^0+1 (4+5-(18/2)^0+1 (4+5-9)^0+1 (0)^0+1 ==> (0)^0 = undefined
Zero raised to power zero is indeterminate. Thus adding 1 to indeterminate = indeterminate.
First we have to have to look at not-always real equations,which is ( 4 + 5 − 3 × 6 ÷ 2 ) 0 and x^0 not real for 0.,but for other number the answer is 1.So let check
( 4 + 5 − 3 × 6 ÷ 2 ) 0
( 9 − 1 8 ÷ 2 ) 0
( 9 − 9 ) 0
0 0
So the answer is Indeterminate which is Undefined
0^0 Is always indeterminate... Only if something tends to 0 is raised to power 0 then it gives 1....
yes i did it correct . pretty easy one! I don't understand why only 13% people could solve it..
How do you know that percetage?
Undefined and indeterminate are VERY different concepts. The is undefined (unless of course if you define it.)
After solving the problem given in the bracket. We get 0^0 which is indeterminate.
if 0^0 is to exist then the statement that 0^0=0^(1-1) should exist. but we all know that 0^-1 is not defined in mathematics. so we cannot define 0^0.
Just apply BODMAS which will get you to 0^0 which is indeterminate .
For any real number "a", a^0 (a to the power 0) can be written as a^(1-1) this means a/a and that is 1. but when a=0 then the form becomes (0/0) where we know that something divided by 0 is undefined. Using VBODMAS we get 1+0^0, so its not determinate.
I don't know if what I'm about to say is 100% correct, but it is what I've been taught and I feel like I should contribute.
For any real number n, that is greater than 0 raised to the power of 0 = 1. Since 49 = 7^2, and if we divide 49 by 7, that is undoing the square. And since 343 = 7^3, dividing 343 by 7 is subtracting 1 from the exponent of 3, and dividing the quotient of 343/7 by another 7 is subtracting another 1 from the exponent. So if we have 7^1 = 1, divided by 7 (to subtract 1 from the exponent), we get 1, so 7^0 = 1.
But for 0, you can't have 0^3, or 0^4. So therefore, 0^1 = 0, and 0/0 = indeterminate (not a number). So even though for any real number n where n<1 to the power of 0 = 1, I don't think it is the case for 0.
Such a tricky question. Zero powered by zero is indeterminate.
Write a solution. 0^0= indeterminate
It should equal 0. If you have nothing, (as in a 0), and then do nothing to it (as in any form of 0), you still have nothing as in 0. ,
Log in to reply
Your explanation implies that 0/0 is 0 though... which is not the case
Log in to reply
How does it imply 0/0? The rule a^m-n = a^m / a^n only applies to non-zero integers.
Log in to reply
@Saad Ghaznavi – I forgot what this is about... but I think it's because of the wording you used. "0/0" is also " nothing doing nothing to it" like you described.
OK. I thought the reason to anything raised to the power zero equals 1 as the following. (a^3)/a = a^2, (a^2)/a = a, a/a = a^0 = 1, But in this case a = 0. 0/0 is indeterminate. So a^0 should be indeterminate.
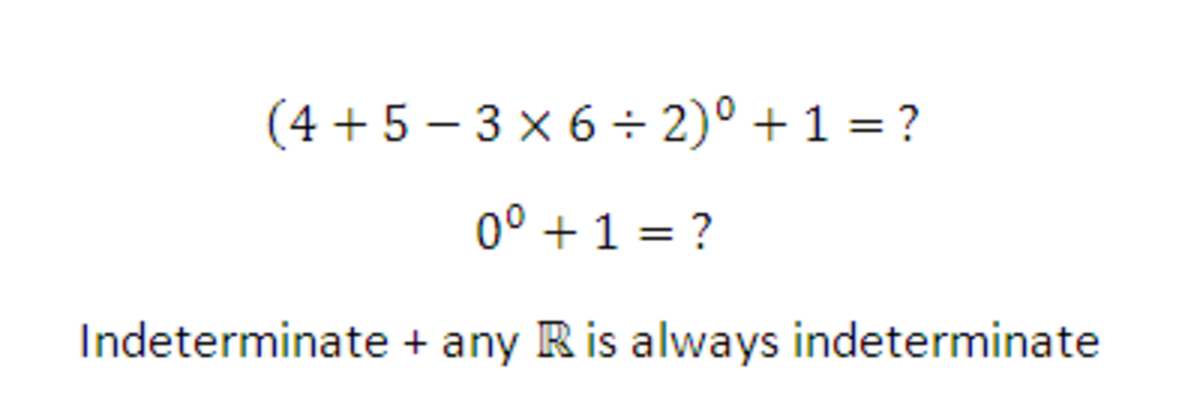
Do not be fooled! Calculate it step by step. 4 + 5 − 3 × 6 ÷ 2 = 9 − 3 × 3 = 0 So the expression simplifies to 0 0 + 1 which is indeterminate on account of the term 0 0 .