#33 Measure Your Calibre
r = 0 ∑ n ( r n ) cos ( r θ ) = ?
Notation: ( N M ) = N ! ( M − N ) ! M ! denotes the binomial coefficient .
Bonus: r = 0 ∑ n ( r n ) ( tan r θ ) = ?
Inspired by Tapas Mazumdar , whose problem was about sines, mine is about cosines.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Sir, what about the bonus?
r
=
0
∑
n
(
r
n
)
cos
r
θ
⟹
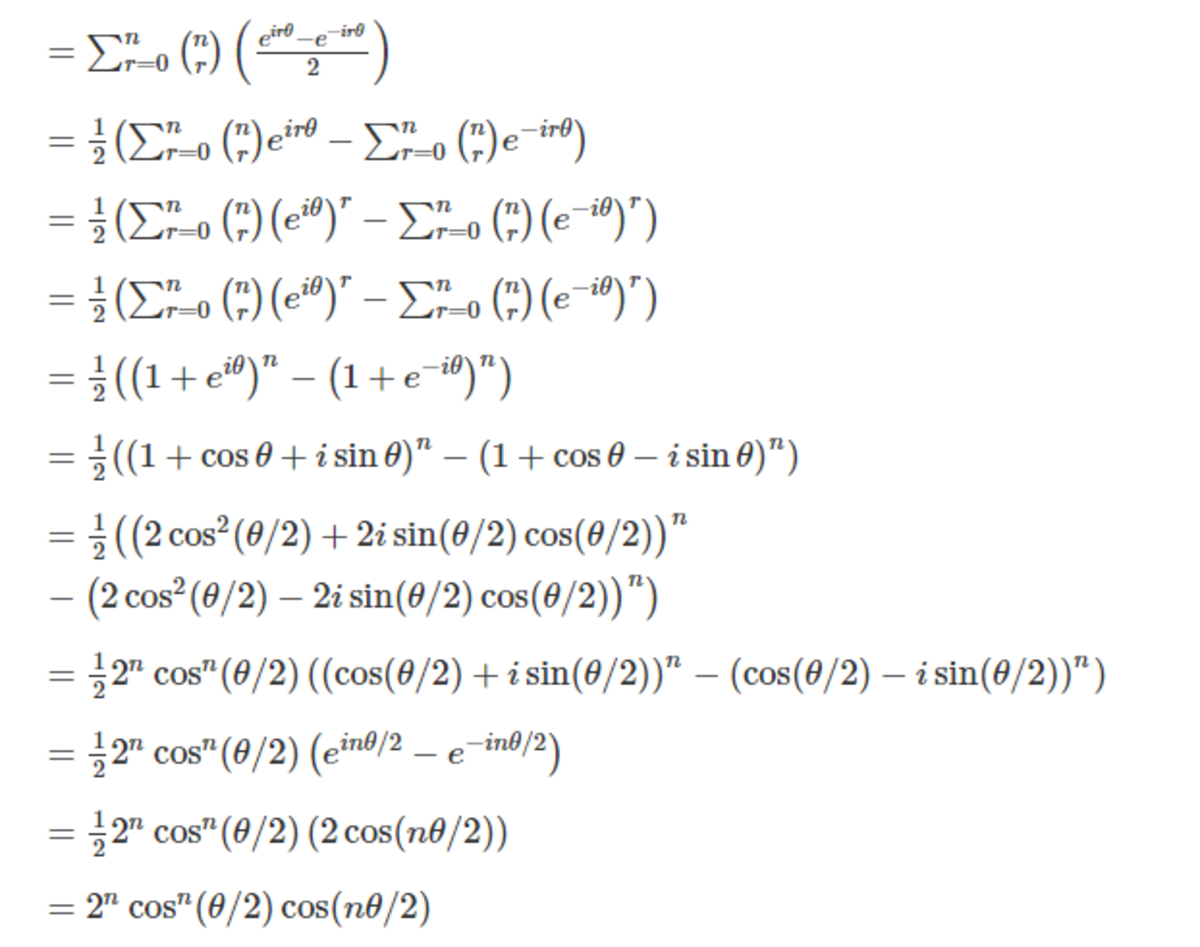
LET ME THINK ABOUT THE BONUS!
Great solution...did the same.
Log in to reply
Thank you brother, Do you have whatsapp?
If so, please share your number, we have whatsapp brilliant group , well add yoi
Log in to reply
No....I don't use whatsapp.
Relevant wiki: Euler's Formula
S = r = 0 ∑ n ( r n ) cos r θ = r = 0 ∑ n ( r n ) ℜ { e i r θ } = ℜ { r = 0 ∑ n ( r n ) e i r θ } = ℜ { ( 1 + e i θ ) n } = ℜ { ( 1 + cos θ + i sin θ ) n } = ℜ { ( 1 + 2 cos 2 2 θ − 1 + 2 i sin 2 θ cos 2 θ ) n } = ℜ { 2 n cos n 2 θ ( cos 2 θ + i sin 2 θ ) n } = ℜ { 2 n cos n 2 θ ⋅ e i 2 n θ } = 2 n cos n 2 θ cos 2 n θ By Euler’s formula: e i x = cos x + i sin x where ℜ { z } is the real part of complex number z .